/MAT/LAW2 (PLAS_JOHNS)

This model expresses material stress as a function of strain, strain rate and temperature. A built-in failure criterion based on the maximum plastic strain is available.

Format

Definitions

Example (Classic Parameter Input)

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
                  Mg                  mm                   s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/PLAS_JOHNS/1/1
Steel
#              RHO_I
              7.8E-9
#                  E                  Nu     Iflag
              210000                  .3         0
#                  a                   b                   n             EPS_max            SIG_max0
                 270               450.0                 0.6                   0                   0
#                  c           EPS_DOT_0       ICC   Fsmooth               F_cut               Chard
                   0                   0         0         0                   0                   0
#                  m              T_melt              rhoC_p                 T_r
                   0                   0                   0                   0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

Example (Simplified Input - Experimental Data)

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
                  Mg                  mm                   s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/PLAS_JOHNS/1/1
Steel (use ultimate tensile stress(UTS) and engineering strain )
#              RHO_I
              7.8E-9
#                  E                  Nu     Iflag
              210000                  .3         1
#              SIG_y                 UTS             EPS_UTS             EPS_max            SIG_max0
                 270               362.8              0.2885                   0                   0
#                  c           EPS_DOT_0       ICC   Fsmooth               F_cut               Chard
                   0                   0         0         0                   0                   0
#                  m              T_melt              rhoC_p                 T_r
                   0                   0                   0                   0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

Comments

1. This is an elasto-plastic material model that includes strain rate and temperature effects with true stress and strain output.
2. In this model the material behaves as a linear-elastic material when the equivalent stress is lower than the plastic yield stress. For higher stress values, the material behavior is plastic, and the true stress is calculated as:(1)
   $$\sigma =\left(a+b{{\epsilon }_p}^n\right)\left(1+c\ln \frac{\dot{\epsilon }}{{\dot{\epsilon }}_0}\right)\left(1-{(T^{\ast })}^m\right)$$
   Where,(2)

   $$T^{*}=\frac{T-T_r}{T_{melt}-T_r}$$
   Where,

   ${\epsilon }_p$

   Plastic strain

   $\dot{\epsilon }$

   Strain rate

   $T$

   Temperature

   T_r

   Ambient temperature

   T_melt

   Melting temperature

3. If I_flag=0, the Johnson-Cook equation parameters a, b, and n values are entered.

   If I_flag=1, experimental engineering stress and stain data can be entered for ${\sigma }_y$ , UTS and ${\epsilon }_{UTS}$ and the parameters a, b and n are calculated and printed in the Starter output file. If the a, b and n parameters cannot be automatically fit, then a Starter warning message will contain important information about changes to the material input.

4. The plastic yield stress should always be greater than zero. To model pure elastic behavior, the plastic yield stress will be set to 10³⁰.
5. When ${\epsilon }_p$ reaches the value of ${\epsilon }_p^{max}$ in one integration point, then based on the element type:
   • Shell elements: The corresponding shell element is deleted.
   • Solid elements: The deviatoric stress of the corresponding integral point is permanently set to 0; however, the solid element is not deleted.
6. The plastic hardening exponent, n must be less than or equal to 1.
7. The strain rate has no effect on truss elements.
8. To eliminate the effect of the strain rate, you can either set the value of c equal to 0 or the reference strain rate ( ${\dot{\epsilon }}_0$ ) can be set equal to 10³⁰. There is no effect of strain rate when $\dot{\epsilon }$ is less than ${\dot{\epsilon }}_0$ .
9. The ICC flag defines the effect of strain rate on the maximum material stress ${\sigma }_{\max }$ . Figure 1 shows the value of for ${\sigma }_{\max }$ the corresponding ICC flag.

   

   $\sigma =\left(a+b{{\epsilon }_p}^n\right)\left(1+c\ln \left(\frac{\dot{\epsilon }}{{\dot{\epsilon }}_o}\right)\right)$	$\sigma =\left(a+b{{\epsilon }_p}^n\right)\left(1+c\ln \left(\frac{\dot{\epsilon }}{{\dot{\epsilon }}_o}\right)\right)$
   ${\sigma }_{\max }={\sigma }_{\max 0}\left(1+c\ln \left(\frac{\dot{\epsilon }}{{\dot{\epsilon }}_o}\right)\right)$	${\sigma }_{\max }={\sigma }_{\max 0}$

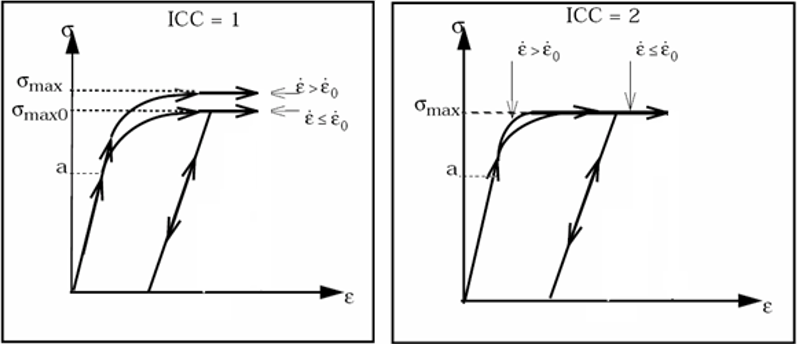   Figure 1.

10. There is no effect of temperature on trusses and beams.
11. The temperature is constant ( $T=T_r$ ), if $\rho C_p=0$ .
12. Adiabatic conditions are assumed for thermal simulations with initial temperature equal to reference temperature (T_r) and:(3)
    $$T=T_r+\frac{E_{\mathrm{int}}}{\rho C_p(Volume)}$$

    Where, E_int is the internal deformation energy.

13. The strain rate coefficient, c and reference strain rate ${\dot{\epsilon }}_0$ must be defined to include thermal effects.
14. When /HEAT/MAT (with I_form=1) references this material model, the values of T_r and $\rho C_p$ defined in this card will be overwritten by the corresponding $T_0$ and $\rho {}_0{C}_p$ defined in /HEAT/MAT.
15. When the temperature is not initialized using /HEAT/MAT or /INITEMP, the reference temperature (T_r) is also the initial temperature.
16. The hardening coefficient is used to describe the hardening model (during unloading). The values of the hardening coefficient should be between 0 and 1.