/MAT/LAW4 (HYD_JCOOK)
Block Format Keyword This law represents an isotropic elasto-plastic material using the Johnson-Cook material model. This model expresses material stress as a function of strain, strain rate and temperature.
This material may account for the nonlinear dependence between pressure and volumetric strain when corresponding equation of state is specified. A built-in failure criterion based on the maximum plastic strain is available. This material law is compatible with solid elements only.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /MAT/LAW4/mat_ID/unit_ID or /MAT/HYD_JCOOK/mat_ID/unit_ID | |||||||||
| mat_title | |||||||||
| E | |||||||||
| a | b | n | |||||||
| Pmin | |||||||||
| c | m | Tmelt | Tmax | ||||||
| Tr | |||||||||
Definitions
| Field | Contents | SI Unit Example |
|---|---|---|
| mat_ID | Material identifier (Integer, maximum 10 digits) |
|
| unit_ID | Unit Identifier (Integer, maximum 10 digits) |
|
| mat_title | Material title (Character, maximum 100 characters) |
|
| Initial density. (Real) |
||
| Reference density used in E.O.S
(equation of state). Default = (Real) |
||
| E | Young's modulus. (Real) |
|
| Poisson's ratio. (Real) |
||
| a | Yield stress. (Real) |
|
| b | Plastic hardening
parameter. (Real) |
|
| n | Plastic hardening exponent. Default = 1.0 (Real) |
|
| Failure plastic strain. Default = 1030 (Real) |
||
| Maximum stress. Default = 1030 (Real) |
||
| Pmin | Pressure cutoff ( < 0 ). Default = -1030 (Real) |
|
| c | Strain rate coefficient.
Default = 0.00 (Real) |
|
| Reference strain rate. If , no strain rate effect. (Real) |
||
| m | Temperature exponent. Default = 1.00 (Real) |
|
| Tmelt | Melting temperature.
Default = 1030 (Real) |
|
| Tmax | For T > Tmax: m = 1 is used. Default = 1030 (Real) |
|
| Specific heat per unit
volume. (Real) |
||
| Tr | Reference temperature. Default = 300K (Real) |
Example
#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
g cm mus
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/HYD_JCOOK/1/1
Aluminum
# RHO_I RHO_0
2.8 0
# E nu
.734 .33
# A B n epsmax sigmax
.0024 .0042 .8 0 .0068
# Pmin
-.0223
# C EPS_DOT_0 M Tmelt Tmax
.062 1E-6 1 1220 0
# RHOCP T_r
2.59E-5 0
/EOS/TILLOTSON/1/1
Aluminum
# C1 C2 A B
.752 .65 .5 1.63
# ER ES VS E0 RHO_0
.135 .081 1.1 0 0
# ALPHA BETA
5 5
/FAIL/JOHNSON/3
# D1 D2 D3 D4 D5
.112 .123 -1.5 .007 0
# EPS_0 Ifail_sh Ifail_so Dadv Ixfem
1E-6 0 1 0 0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|Comments
- In this model, the material
behaves as a linear-elastic material when the equivalent stress is lower than the plastic
yield stress. For higher stress values, the material behavior is plastic and the stress is
calculated as:
(1) Where,(2) Where,- Plastic strain
- Strain rate
- T
- Temperature
- Tr
- Reference temperature
- Tmelt
- Melting temperature
When /HEAT/MAT (with Iform = 1) references this material model, the values of Tr and Tmelt defined in this card will be overwritten by the corresponding T0 and Tmelt defined in /HEAT/MAT.
When the temperature is not initialized using /HEAT/MAT or /INITEMP, the reference temperature (Tr) is also the initial temperature.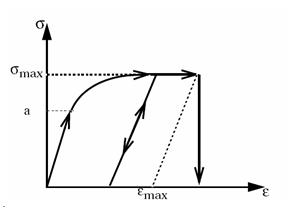
Figure 1. - The plastic yield stress should always be greater than zero. To model pure elastic behavior, the plastic yield stress will be set to 1030.
- When reaches the value of (for tension, compression or shear), in one integration point, the deviatoric stress of the corresponding integration point is permanently set to 0, however, the solid element is not deleted.
- The plastic hardening exponent, n, must be less than or equal to 1.
- To eliminate the effect of the strain rate, either set the value of c equal to 0 or set the reference strain rate ( ) equal to 1030. There is no effect of strain rate when is less than .
- By default, the hydrostatic
pressure is linearly proportional to volumetric strain:
(3) Where, is the bulk modulus and is the volumetric strain.
An additional Equation of State (/EOS) card can refer to this material in order to incorporate a nonlinear dependency between hydrostatic pressure and volumetric strain.