/MAT/LAW43 (HILL_TAB)

Format

Definitions

Example (Metal)

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
                 Mg                  mm                  ms
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/HILL_TAB/1/1
metal
#              RHO_I
                  80
#                  E                  NU
              206000                  .3
#FUNCT_IDE                          EINF                  CE
         0                             0                   0
#                r00                 r45                 r90              C_hard   Iyield0
                1.73                1.34                2.24                   0         0
#           EPSP_max              EPS_t1               EPS_m
                   0                   0                   0
# func_IDi                      Fscale_i           EPS_dot_i
         5                             0                   0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  3. FUNCTIONS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/5
metal
#                  X                   Y
                  0                 260                                                           
               .002                 270                                                           
               .005                 280                                                           
                .01                 297                                                           
                .02                 322                                                           
                .05                 370                                             
                 .1                 422                                                 
                .15                 457                                           
                 .2                 485                                         
                 .3                 528                                                           
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

Comments

1. This material law must be used with property set /PROP/TYPE9 (SH_ORTH) or /PROP/TYPE10 (SH_COMP).
2. The yield stress is defined by a user function and the yield stress is compared to equivalent stress:(1)
   $${\sigma }_{eq}=\sqrt{A_1{\sigma }_1^2+A_2{\sigma }_2^2-A_3{\sigma }_1{\sigma }_2+A_{12}{\sigma }_{12}^2}$$
3. Angles for Lankford parameters are defined with respect to orthotropic direction 1.(2)
   $$\begin{array}{ll}R=\frac{r_{00}+2r_{45}+r_{90}}{4}& H=\frac{R}{1+R}\\ A_1=H\left(1+\frac{1}{r_{00}}\right)& A_2=H\left(1+\frac{1}{r_{90}}\right)\\ A_3=2H& A_{12}=2H(r_{45}+0.5)\left(\frac{1}{r_{00}}+\frac{1}{r_{90}}\right)\\ r_{00}=\frac{A_3}{2A_1-A_3}& r_{45}=\frac{1}{2}\left(\frac{A_{12}}{A_1+A_2-A_3}-1\right)\\ r_{90}=\frac{A_3}{2A_2-A_3}& \end{array}$$

   The Lankford parameters r_a is the ratio of plastic strain in plane and plastic strain in thickness direction ${\epsilon }_{33}$ .

   (3)
   $$r_{\alpha }=\frac{d{\epsilon }_{\alpha +\pi /2}}{d{\epsilon }_{33}}$$

   Where, α is the angle to the orthotropic direction 1.

   This Lankford parameters r_a could be determined from a simple tensile test at an angle α.

   A higher value of R means better formability.

4. If the last point of the first (static) function equals 0 in stress, default value of ${\epsilon }_p^{max}$ is set to the corresponding value of ${\epsilon }_p$ .
5. Element deletion:
   • Once ${\epsilon }_p$ (plastic strain) reaches ${\epsilon }_p^{max}$ , in one integration point, the element is deleted.
   • If ${\epsilon }_1$ reaches ${\epsilon }_t$ , the stress is reduced using the following relation: (4)
     $$\sigma =\sigma \left(\frac{{\epsilon }_m-{\epsilon }_1}{{\epsilon }_m-{\epsilon }_t}\right)$$
   • If ${\epsilon }_1$ (largest principal strain) reaches ${\epsilon }_m$ ( ${\epsilon }_1>{\epsilon }_m$ ), the stress in element is reduced to 0 (but the element is not deleted).
   • Once ${\epsilon }_1$ (largest principal strain) reaches ${\epsilon }_f$ (maximum tensile failure strain), the element is deleted.
6. The maximum number of curves that can be input is 10.
7. If $\dot{\epsilon }\le {\dot{\epsilon }}_n$ , the yield is interpolated between $f_n$ and $f_{n-1}$ .
8. If $\dot{\epsilon }\le {\dot{\epsilon }}_1$ , function $f_1$ is used.
9. Above ${\dot{\epsilon }}_{\max }$ , yield is extrapolated.

   
   
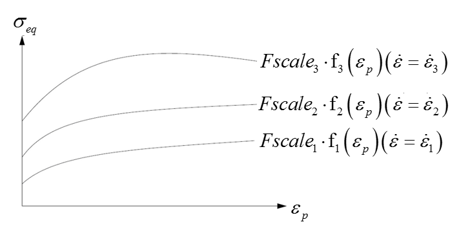
   Figure 1.

10. Radial return is not available (only iterative plasticity).
11. If the yield stresses have been obtained in the orthotropic direction 1, define I_yield0 =1; otherwise I_yield0 =0.
12. The evolution of Young's modulus:
    • If fct_ID_E > 0, the curve defines a scale factor for Young's modulus evolution with equivalent plastic strain ${\overline{\epsilon }}_p$ , which means the Young's modulus is scaled by the function $\text{f}\left({\overline{\epsilon }}_p\right)$ :(5)
      $$\text{E}\left(t\right)=\text{f}\left({\overline{\epsilon }}_p\right)E$$

      The initial value of the scale factor should be equal to 1 and it decreases.

    • If fct_ID_E = 0, the Young's modulus is calculated as:(6)
      $$\mathrm{E}\left(t\right)=E-(E-E_{\inf })\left(1-\exp (-C_E{\overline{\epsilon }}_p)\right)$$

      Where, $E$ and $E_{\inf }$ are respectively the initial and asymptotic value of Young's modulus, and ${\overline{\epsilon }}_p$ is the accumulated equivalent plastic strain.

      Note:

      If fct_ID_E = 0 and C_E = 0, Young's modulus E is kept constant.