/MAT/LAW36 (PLAS_TAB)

Format

Definitions

Field	Contents	SI Unit Example
mat_ID	Material identifier. (Integer, maximum 10 digits)
unit_ID	Unit Identifier. (Integer, maximum 10 digits)
mat_title	Material title. (Character, maximum 100 characters)
${\rho }_i$	Initial density. (Real)	$\left[\frac{\text{kg}}{{\text{m}}^3}\right]$
E	Young's modulus. (Real)	$\left[\text{Pa}\right]$
$\nu$	Poisson's ratio. (Real)
${\epsilon }_p^{max}$	Failure plastic strain. Default = 1020 (Real)
${\epsilon }_t$	Tensile failure strain at which stress starts to reduce. Default = 1020 (Real)
${\epsilon }_m$	Maximum tensile failure strain at which the stress in element is set to zero. Default = 2.0 x 1020 (Real)
Nfunct	Number of functions ($1\le N_{funct}\le 100$ ). (Integer)
Fsmooth	Smooth strain rate option flag. = 0 (Default) No strain rate smoothing. = 1 Strain rate smoothing active. (Integer)
Chard	Hardening coefficient. = 0 Hardening is a full isotropic model. = 1 Hardening uses the kinematic Prager-Ziegler model. = value between 0 and 1 Hardening is interpolated between the two models. (Real)
Fcut	Cutoff frequency for strain rate filtering. Only available for shell and solid elements, Appendix: Filtering. Default = 1.0 x 1020 (Real)	$\text{[Hz]}$
VP	Strain rate choice flag. = 0 (Default) Strain rate effect on yield stress depends on the total strain rate. = 1 Strain rate effect on yield depends on the plastic strain rate. In this case, there is no strain rate filtering, so Fsmooth and Fcut are not used. (Integer)
${\epsilon }_f$	Tensile strain for element deletion. Default = 3.0 x 1020 (Real)
fct_IDp	Yield factor vs. pressure function. 7 Default = 0 (Integer)
Fscale	Scale factor for yield factor in fct_IDp. Default = 1.0 (Real)	$\left[\text{Pa}\right]$
fct_IDE	Function identifier for the scale factor of Young's modulus, when Young's modulus is function of the plastic strain. Default = 0: in this case the evolution of Young's modulus depends on Eint and CE. (Integer)
Eint	Saturated Young's modulus for infinitive plastic strain. (Real)
CE	Parameter for Young's modulus evolution. (Real)
fct_ID1	Yield stress function identifier 1 corresponding to strain rate ${\dot{\epsilon }}_1$ . (Integer)
fct_ID2	Yield stress function identifier 2 corresponding to strain rate ${\dot{\epsilon }}_2$ . (Integer)
fct_ID3	Yield stress function identifier 3 corresponding to strain rate ${\dot{\epsilon }}_3$ . (Integer)
fct_ID4	Yield stress function identifier 4 corresponding to strain rate ${\dot{\epsilon }}_4$ . (Integer)
fct_ID5	Yield stress function identifier 5 corresponding to strain rate ${\dot{\epsilon }}_5$ . (Integer)
Fscale1	Scale factor for ordinate (stress) in fct_ID1. Default = 1.0 (Real)	$\left[\text{Pa}\right]$
Fscale2	Scale factor for ordinate (stress) in fct_ID2. Default = 1.0 (Real)	$\left[\text{Pa}\right]$
Fscale3	Scale factor for ordinate (stress) in fct_ID3. Default = 1.0 (Real)	$\left[\text{Pa}\right]$
Fscale4	Scale factor for ordinate (stress) in fct_ID4. Default = 1.0 (Real)	$\left[\text{Pa}\right]$
Fscale5	Scale factor for ordinate (stress) in fct_ID5. Default = 1.0 (Real)	$\left[\text{Pa}\right]$
${\dot{\epsilon }}_1$	If VP =0 total strain rate for fct_ID1. If VP =1 plastic strain rate for fct_ID1. (Real)	$\left[\frac{\text{1}}{\text{s}}\right]$
${\dot{\epsilon }}_2$	If VP =0 total strain rate for fct_ID2. If VP =1 plastic strain rate for fct_ID2. (Real)	$\left[\frac{\text{1}}{\text{s}}\right]$
${\dot{\epsilon }}_3$	If VP =0 total strain rate for fct_ID3. If VP =1 plastic strain rate for fct_ID3. (Real)	$\left[\frac{\text{1}}{\text{s}}\right]$
${\dot{\epsilon }}_4$	If VP =0 total strain rate for fct_ID4. If VP =1 plastic strain rate for fct_ID4. (Real)	$\left[\frac{\text{1}}{\text{s}}\right]$
${\dot{\epsilon }}_5$	If VP =0 total strain rate for fct_ID5. If VP =1 plastic strain rate for fct_ID5. (Real)	$\left[\frac{\text{1}}{\text{s}}\right]$

Example (Aluminum)

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
                   g                  mm                  ms
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/PLAS_TAB/1/1
Aluminium_example
#              RHO_I
               .0027                   0
#                  E                  Nu           Eps_p_max               Eps_t               Eps_m
               60400                 .33                   0                   0                   0
#  N_funct  F_smooth              C_hard               F_cut               Eps_f                  VP
        14         0                   0                   0                   0                   0
#  fct_IDp              Fscale   Fct_IDE                EInf                  CE
         0                   0         0                   0                   0
# func_ID1  func_ID2  func_ID3  func_ID4  func_ID5
         1         2         3         4         5
         6         7         8         9        10
        11        12        13        14
#           Fscale_1            Fscale_2            Fscale_3            Fscale_4            Fscale_5
                   1                 1.2                 1.4                 1.6                 1.9
                  10                10.2                10.4                10.6                10.9
                  20                20.2                20.4                20.6
#          Eps_dot_1           Eps_dot_2           Eps_dot_3           Eps_dot_4           Eps_dot_5
                   0                  20                  30                  40                  50
                 110                 120                 130                 140                 150
                 210                 220                 230                 240
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  3. FUNCTIONS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/1
function_36
#                  X                   Y
                   0                  90                                                            
              2.5E-4                 100                                                           
                .001                 104                                                           
                .009                 121                                                            
                .017                 136                                                            
                .021                 143                                                           
                .036                 156                                                           
                .045                 162                                                         
                .055                 165                                                           
                .072                 170                                                           
                .075                 170                                                          
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/2
function_36
#                  X                   Y
                   0                  90                                                            
              2.5E-4                 100                                                           
                .001                 104                                                           
                .009                 121                                                            
                .017                 136                                                            
                .021                 143                                                           
                .036                 156                                                           
                .045                 162                                                         
                .055                 165                                                           
                .072                 170                                                           
                .075                 170                                                            
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/3
function_36
#                  X                   Y
                   0                  90                                                            
              2.5E-4                 100                                                           
                .001                 104                                                           
                .009                 121                                                            
                .017                 136                                                            
                .021                 143                                                           
                .036                 156                                                           
                .045                 162                                                         
                .055                 165                                                           
                .072                 170                                                           
                .075                 170                                                           
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/4
function_36
#                  X                   Y
                   0                  90                                                            
              2.5E-4                 100                                                           
                .001                 104                                                           
                .009                 121                                                            
                .017                 136                                                            
                .021                 143                                                           
                .036                 156                                                           
                .045                 162                                                         
                .055                 165                                                           
                .072                 170                                                           
                .075                 170                                                           
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/5
function_36
#                  X                   Y
                   0                  90                                                            
              2.5E-4                 100                                                           
                .001                 104                                                           
                .009                 121                                                            
                .017                 136                                                            
                .021                 143                                                           
                .036                 156                                                           
                .045                 162                                                         
                .055                 165                                                           
                .072                 170                                                           
                .075                 170                                                            
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/6
function_36
#                  X                   Y
                   0                  90                                                            
              2.5E-4                 100                                                           
                .001                 104                                                           
                .009                 121                                                            
                .017                 136                                                            
                .021                 143                                                           
                .036                 156                                                           
                .045                 162                                                         
                .055                 165                                                           
                .072                 170                                                           
                .075                 170                                                           
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/7
function_36
#                  X                   Y
                   0                  90                                                            
              2.5E-4                 100                                                           
                .001                 104                                                           
                .009                 121                                                            
                .017                 136                                                            
                .021                 143                                                           
                .036                 156                                                           
                .045                 162                                                         
                .055                 165                                                           
                .072                 170                                                           
                .075                 170                                                           
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/8
function_36
#                  X                   Y
                   0                  90                                                            
              2.5E-4                 100                                                           
                .001                 104                                                           
                .009                 121                                                            
                .017                 136                                                            
                .021                 143                                                           
                .036                 156                                                           
                .045                 162                                                         
                .055                 165                                                           
                .072                 170                                                           
                .075                 170                                                            
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/9
function_36
#                  X                   Y
                   0                  90                                                            
              2.5E-4                 100                                                           
                .001                 104                                                           
                .009                 121                                                            
                .017                 136                                                            
                .021                 143                                                           
                .036                 156                                                           
                .045                 162                                                         
                .055                 165                                                           
                .072                 170                                                           
                .075                 170                                                           
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/10
function_36
#                  X                   Y
                   0                  90                                                            
              2.5E-4                 100                                                           
                .001                 104                                                           
                .009                 121                                                            
                .017                 136                                                            
                .021                 143                                                           
                .036                 156                                                           
                .045                 162                                                         
                .055                 165                                                           
                .072                 170                                                           
                .075                 170                                                           
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/11
function_36
#                  X                   Y
                   0                  90                                                            
              2.5E-4                 100                                                           
                .001                 104                                                           
                .009                 121                                                            
                .017                 136                                                            
                .021                 143                                                           
                .036                 156                                                           
                .045                 162                                                         
                .055                 165                                                           
                .072                 170                                                           
                .075                 170                                                           
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/12
function_36
#                  X                   Y
                   0                  90                                                            
              2.5E-4                 100                                                           
                .001                 104                                                           
                .009                 121                                                            
                .017                 136                                                            
                .021                 143                                                           
                .036                 156                                                           
                .045                 162                                                         
                .055                 165                                                           
                .072                 170                                                           
                .075                 170                                                           
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/13
function_36
#                  X                   Y
                   0                  90                                                            
              2.5E-4                 100                                                           
                .001                 104                                                           
                .009                 121                                                            
                .017                 136                                                            
                .021                 143                                                           
                .036                 156                                                           
                .045                 162                                                         
                .055                 165                                                           
                .072                 170                                                           
                .075                 170                                                            
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/14
function_36
#                  X                   Y
                   0                  90                                                            
              2.5E-4                 100                                                           
                .001                 104                                                           
                .009                 121                                                            
                .017                 136                                                            
                .021                 143                                                           
                .036                 156                                                           
                .045                 162                                                         
                .055                 165                                                           
                .072                 170                                                           
                .075                 170                                                           
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

Comments

1. The first point of yield stress functions (plastic strain vs stress) should have a plastic strain value of zero. If the last point of the first (static) function equals 0 in stress, default value of ${\epsilon }_p^{max}$ is set to the corresponding value of ${\epsilon }_p$ .
2. Element deletion:
   • Once ${\epsilon }_p$ (plastic strain) reaches ${\epsilon }_p^{max}$ , in one integration point, the element is deleted.
   • If ${\epsilon }_1$ reaches ${\epsilon }_t$ , the stress is reduced using the following relation: (1)
     $$\sigma =\sigma \left(\frac{{\epsilon }_m-{\epsilon }_1}{{\epsilon }_m-{\epsilon }_t}\right)$$
   • If ${\epsilon }_1$ (largest principal strain) reaches ${\epsilon }_m$ ( ${\epsilon }_1>{\epsilon }_m$ ), the stress in element is reduced to 0 (but the element is not deleted).
   • Once ${\epsilon }_1$ (largest principal strain) reaches ${\epsilon }_f$ (maximum tensile failure strain), the element is deleted.
3. The kinematic hardening model is not available in global formulation (N=0 in shell property keyword) that is, hardening is fully isotropic.
4. In case of kinematic hardening and strain rate dependency, the yield stress depends on the strain rate.
5. Strain rate filtering is used to smooth strain rates.
6. The first function in fct_ID₁ is used for strain rate values from 0 to its corresponding strain rate, strain rate 1. However, the last function used in the model does not extend to the maximum strain rate; for higher strain rates, a linear extrapolation will be applied. This could lead to instability and/or unusual deformation. This instability can be overcome by repeating the stress strain curve, corresponding to the last strain rate, again with a much higher strain rate.

   
   
   Figure 1.

7. fct_ID_p is used to distinguish the behavior in tension and compression for certain materials (pressure dependent yield). This is available for both shell and solid elements. The effective yield stress is then obtained by multiplying the nominal yield stress by the yield factor corresponding to the actual pressure.
8. If $\dot{\epsilon }\le {\dot{\epsilon }}_n$ , the yield stress is interpolated between ${\mathrm{f}}_n$ and ${\mathrm{f}}_{n-1}$ .
9. If $\dot{\epsilon }\le {\dot{\epsilon }}_1$ , function ${\mathrm{f}}_1$ is used.
10. Above ${\dot{\epsilon }}_{\max }$ , yield stress is extrapolated.

    
    
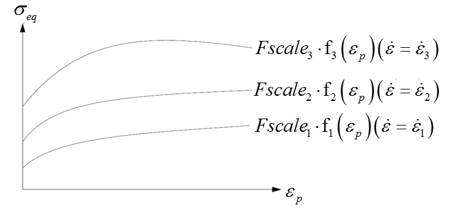
    Figure 2.

    Where,

    $\dot{\epsilon }$

    Total strain rate for VP =0

    $\dot{\epsilon }$

    Plastic strain rate for VP =1

11. Separate functions must be defined for different strain rates.
12. Strain rate values must be given in strictly ascending order.
13. The evolution of Young's modulus:
    • If fct_ID_E > 0, the curve defines a scale factor for Young's modulus evolution with equivalent plastic strain, which means the Young's modulus is scaled by the function $\text{f}\left({\overline{\epsilon }}_p\right)$ : (2)
      $$\mathrm{E}\left(t\right)=f\left({\overline{\epsilon }}_p\right)E$$

      The initial value of the scale factor should be equal to 1 and it decreases.

    • If fct_ID_E = 0, the Young's modulus is calculated as:(3)
      $$\mathrm{E}\left(t\right)=E-(E-E_{\inf })\left(1-\exp (-C_E{\overline{\epsilon }}_p)\right)$$
      Where, $E$ and $E_{\inf }$ are respectively the initial and asymptotic value of Young's modulus, and ${\overline{\epsilon }}_p$ is the accumulated equivalent plastic strain.

      Note: If fct_ID_E = 0 and $C_E$ = 0, Young's modulus $E$ is kept constant.