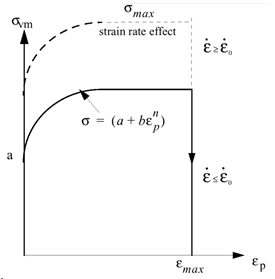
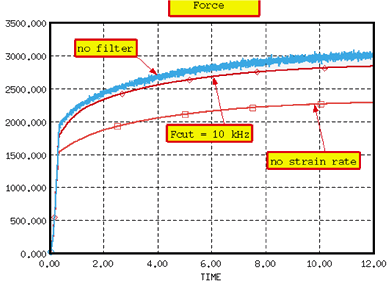
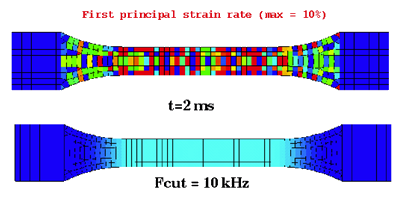
The strain rates exhibit very high frequency vibrations which are not physical. The
strain rate filtering option will enable to damp those oscillations and; therefore obtain
more physical strain rate values.
If there is no strain rate filtering, the equivalent strain rate is the maximum value
of the strain rate components:(7)
For thin-walled structures, the equivalent strain is computed by the following
approach. If ε is the main component of strain tensor, the kinematic assumptions of
thin-walled structures allows to decompose the in-plane strain into membrane and
flexural deformations:(8)
Then, the expression of internal energy can by written as:
(9)
Therefore:(10)
The expression can be simplified to:
(11)
(12)
The expression of the strain rate is derived from
Equation 8:
(13)
Admitting the assumption that the strain rate is proportional to the strain,
i.e.:(14)
(15)
Therefore:(16)
Referring to
Equation 12, it can be seen that
an equivalent strain rate can be defined using a similar expression to the
equivalent strain:
(17)
(18)
For solid elements, the strain rate is computed using the maximum element
stretch:(19)
The strain rate at integration point,
in
/ANIM/TENS/EPSDOT/i
is calculated by:
(20)
Where,
- Membrane strain rate /ANIM/TENS/EPSDOT/MEMB
- Bending strain rate /ANIM/TENS/EPSDOT/BEND.
The strain rate in upper and lower layers is computed by:(21)
/ANIM/TENS/EPSDOT/UPPER(22)
/ANIM/TENS/EPSDOT/LOWER
The strain rate is filtered by using:(23)
Where,
- Time interval
- Fcut
- Cutting frequency
- Filtered strain rate