RD-E: 2202 Ditching using ALE (Mono-Domain)

Units: mm, ms, KN, GPa, kg

Impact of a triangular object on water is performed and the results are compared qualitatively ², also using the experimental data obtained from the Politechnico di Milano. ¹

The computation is performed using several impact velocities of 3.5 and 11 m/s.

The material law for water is BIPHAS law (/MAT/LAW37) with the following characteristics:

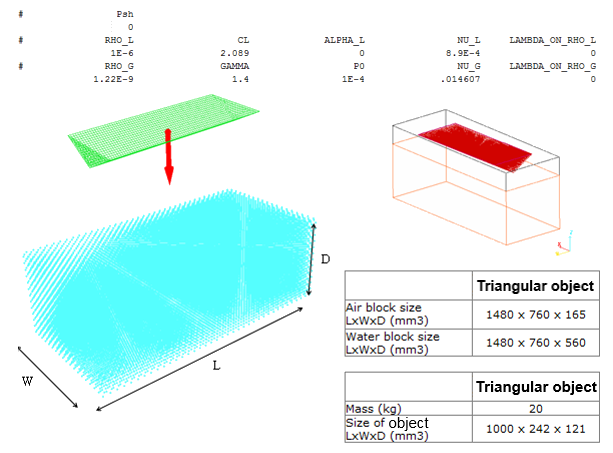
Figure 1. Problem Data

Model Method

The object is modeled using shell elements with an average mesh size of 15 x 15 mm². In order to simplify the computation, it is put in a rigid body with an accelerometer on the main node.

The water is modeled using 15x15x15 mm mesh with a total of 166023 elements.

#            Psh
               0   
#          RHO_L              CL       ALPHA_L         NU_L     LAMBDA_ON_RHO_L
            1e-6           2.089             0       .00089                   0
#          RHO_G           GAMMA            P0         NU_G     LAMBDA_ON_RHO_G
         1.22E-9             1.4         .1e-3      .014607                   0

An interface TYPE18 is defined to manage the contact between the solid in Lagrangian mesh (Prism) and the fluid (pool). The diedra is defined as main and the nodes in the pool (air and water) as secondary.

The interface TYPE18 forces are computed by Penalty method. The interface stiffness is proportional to impact velocity. The results obtained by the ALE approach can be highly dependent to the interface stiffness factor Stfac, which should be adjusted in function of size of element and fluid properties.

The interface TYPE18 forces are computed by Penalty method. The forces are proportional to the stiffness factor Stfac which should be calibrated. Figure 2 shows the dependence of results (acceleration at the accelerometer) to the mesh and Stfac.

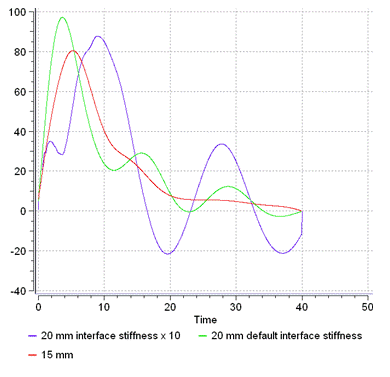
Figure 2. Higher Peak Force with Coarse Mesh and Interface Stiffness Dependence

Higher peak forces are obtained with the coarse mesh. That can be partially corrected by filtering (Figure 3).

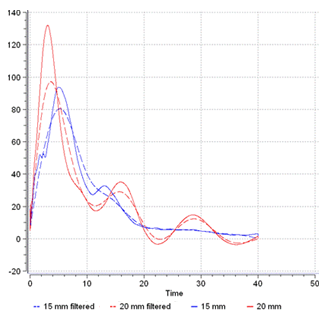
Figure 3. Filtering of Results for Coarse and Fine Meshes

Using a filter CFC 60, -3 dB, the simulation results of the ALE and SPH approaches are compared to Von Karman theoretical solution and experimental measures in Figure 4.

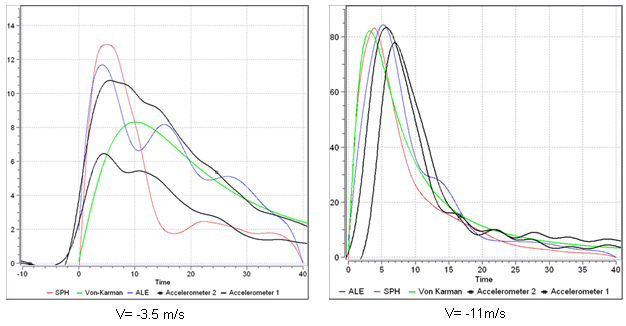
Figure 4. Comparison Between Simulation Results, Theoretical Solution and Experimental Measures (acceleration)

SPH and ALE approaches respectively give the maximum acceleration of 83g and 84g. However, the Von Karman theory delivers 82g; with the maximum value by experience is between 83g and 73g.