RD-E: 2203 Ditching using Multi-Domain for SPH and ALE

Impact of a simple object on water using Multi-Domain to approach SPH and ALE.

The problem consists of a simple object falling into water simulating the ditching of a helicopter.

Options and Keywords Used

/SUBDOMAIN in Multi-Domain
/RAD2RAD/ON in Engine

Input Files

The input files used in this example include:

SPH (Multi-Domain): <install_directory>/hwsolvers/demos/radioss/example/22_Ditching/Ditching_Multi_Domain_SPH/*
ALE (Multi-Domain): <install_directory>/hwsolvers/demos/radioss/example/22_Ditching/Ditching_Multi_Domain_ALE/*

Model Description

Unit: mm, ms, KN, GPa, kg

Use Example 2201 as SPH ditching and Example 2202 as ALE ditching, then add Multi-Domain approach in SPH ditching and ALE ditching

Model Method of Multi-Domain (Single Input Format) Approach

For Multi-Domain approach, take the model of Mono-Domain and:

Setup /SUBDOMAIN in Starter:
- Use /SUBDOMAIN to define sub-domain. In this example part ID 19 is defined as sub-domain.
- For SPH ditching:
  
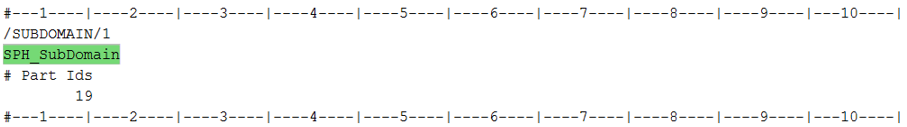
  Figure 1.
- For ALE ditching:
  
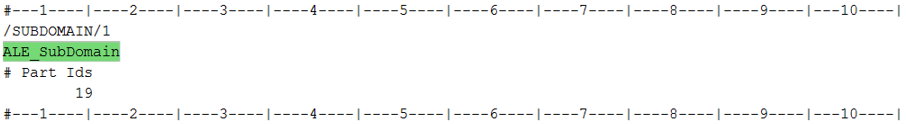
  Figure 2.
  
  Note: The subdomain_title "SPH_SubDomain" (or "ALE_SubDomain") must be the same as sub-domain Engine name SPH_SubDomain_0001.rad (or ALE_SubDomain_0001.rad).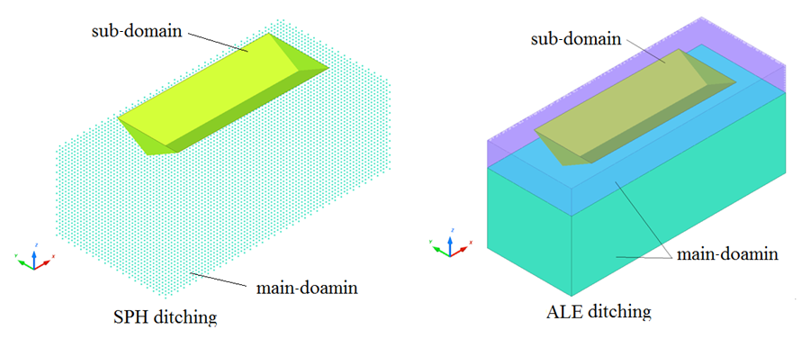
  
  Figure 3. Domain Description in Multi-Domain Approach
Setup in two Engine files:
- First Engine file (main-domain):
  - Take the Engine of Mono-Domain and insert /RAD2RAD/ON keyword.
  - Free element time step control for ALE or free nodal time step control for SPH in the first Engine file.
- Second Engine file (sub-domain):
  - Take the Engine of Mono-Domain and insert /RAD2RAD/ON keyword.
  - Update the Engine name and also the run name in /RUN. They must match the subdomain_title in Starter /SUBDOMAIN.
  - Set the Lagrange parts (part ID 19) specific time step control
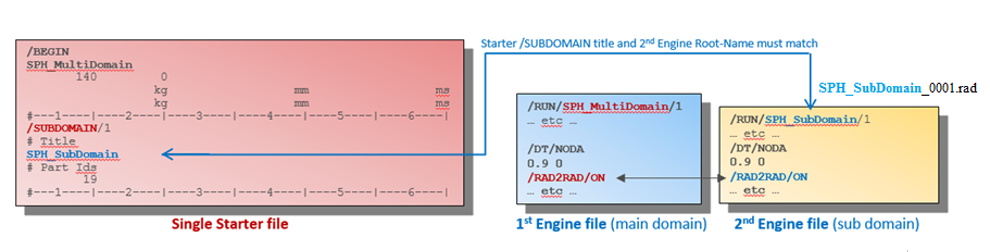
Figure 4. Multi-Domain Setup in Starter and Engine (SPH ditching as example)

Contact Between Main-domain and Sub-domain

As of Radioss version 14.0, Starter automatically creates coupling links between domains with Multi-Domain Single Input Format. In SPH, ditching using /INTER/TYPE7 coupling links between Lagrange sub-domain and SPH main-domain are automatically created. In ALE, ditching using /INTER/TYPE18 coupling links between Lagrange sub-domain and ALE main-domain are automatically created.

Results

Results between Mono-Domain and Multi-Domain

To compare the results between Mono-Domain and Multi-Domain, take the model with 11m/s in initial velocity in SPH ditching and in ALE ditching.

It shows same results for Mono-Domain and Multi-Domain.

Energy comparison between Mono-Domain and Multi-Domain

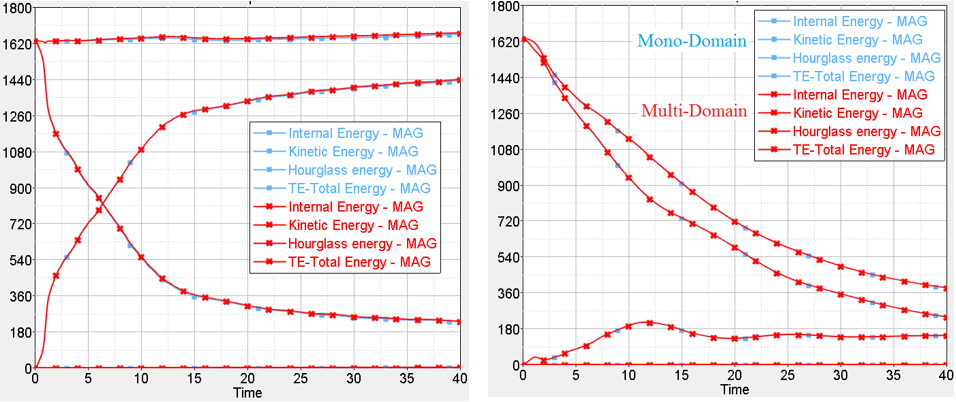
Figure 5. Left: SPH Ditching; Right: ALE Ditching
Acceleration comparison between Mono-Domain and Multi-Domain

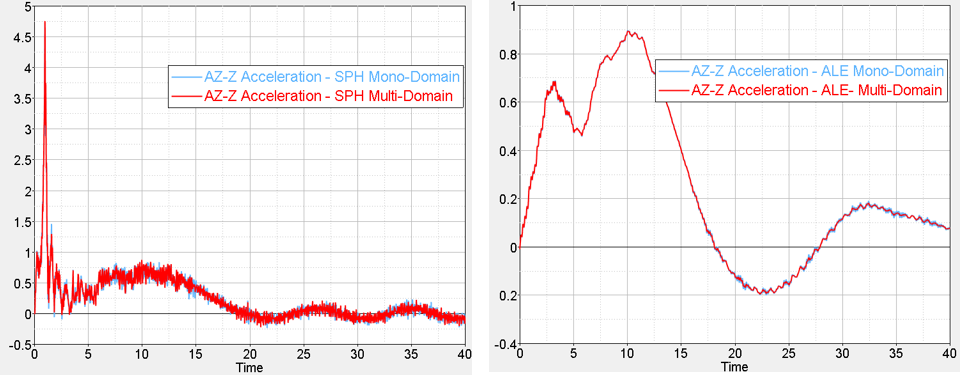
Figure 6. Left: SPH Ditching; Right: ALE Ditching

The time step in Multi-Domain is much bigger than in Mono-Domain.
Time step comparison between Mono-Domain and Multi-Domain

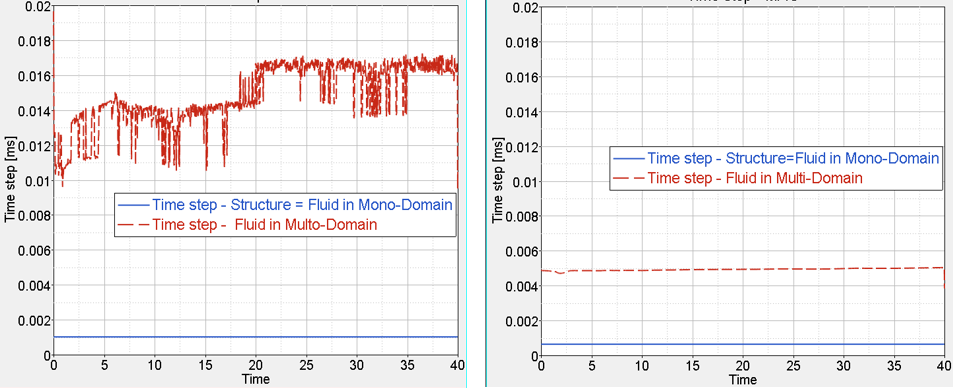
Figure 7. Left: SPH Ditching; Right: ALE Ditching

Theoretical speedup α formula: (1) $α = \frac{T_{M o n o}}{T_{M u l t i}} = \frac{N e_{F l u i d} \cdot C_{F l u i d} \cdot N c_{S t r u c t} + N e_{S t r u c t} \cdot C_{S t r u c t} \cdot N c_{S t r u c t}}{N e_{F l u i d} \cdot C_{F l u i d} \cdot N c_{F l u i d} + N e_{S t r u c t} \cdot C_{S t r u c t} \cdot N c_{S t r u c t}}$

Where,

$N e$

Number of elements

$N c$

Number of cycles

$C$

Element average time cost/cycle
Speedup α could also be formulated with following factors:
- Relative element number:(2) $ψ = \frac{N e_{S t r u c t}}{N e_{S t r u c t} + N e_{F l u i d}}$
- Relative time step (relative cycle numbers):(3) $γ = \frac{d t_{S t r u c t}}{d t_{F l u i d}} = \frac{N c_{F l u i d}}{N c_{S t r u c t}}$
  with
  
  $d t$
  
  Time step
- Relative cost per cycle:(4) $ξ = \frac{C_{F l u i d}}{C_{S t r u c t}}$
  
  Lagrange shell
  
  = 1
  
  Lagrange solid
  
  ~ 3
  
  ALE solid
  
  ~ 6
  
  SPH cell
  
  ~ 15
Then speedup α will be:(5) $α = \frac{ξ + (1 - ξ) \cdot ψ}{ξ \cdot γ + (1 - ξ \cdot γ) \cdot ψ} = \frac{e l a s p e d \begin{matrix} \end{matrix} t i m e \begin{matrix} \end{matrix} i n \begin{matrix} \end{matrix} M o n o D o m a i n}{e l a s p e d \begin{matrix} \end{matrix} t i m e \begin{matrix} \end{matrix} i n \begin{matrix} \end{matrix} M u l t i D o m a i n}$

Elapsed times: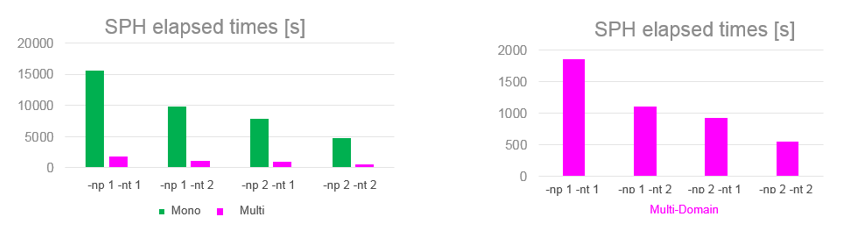

Figure 8. SPH Ditching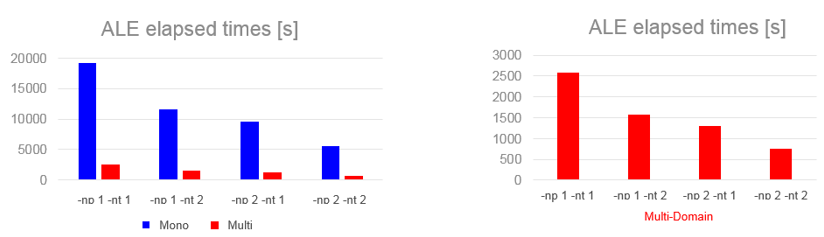

Figure 9. ALE Ditching

After comparing the elapsed time, observe Multi-Domain FSI speedups ranging from 6 times to 9 times of the Mono-Domain.

Conclusion

The Multi-Domain is particularly adapted to FSI simulations involving a large amount of either ALE elements or SPH cells which the time steps are significantly higher than the one in the much smaller in terms of elements of the Lagrange structure
The easiness of setup makes the Multi-Domain applied to FSI much simpler than when applied to purely Lagrange models where the cross-domain contacts need to be minimized as long as this aspect is not automated
Due to this setup easiness the Multi-Domain results in FSI give less possibility to deviations when compared to classical mono-domain results
FSI simulations often involving large ALE or SPH domains with high time steps the Multi-Domain speedups are significantly higher than in pure Lagrange simulations like in Crash

Comments

For Multi-Domain FSI there is no need to minimize the contacts in TYPE7 interface (SPH) or in TYPE18 or TYPE22 interfaces (ALE) between Fluid and Structure whereas it is needed in pure Lagrange Multi-Domain.
For Multi-Domain FSI it is advised to use for the main-domain a free element time step with a scaling factor of 0.5 for ALE and a free nodal time step with a scaling factor of 0.6.
When Lagrange parts are assembled using tied contact interface TYPE2, then poor performances may occur with Spot_flag = 0 or 1.
- Set Spot_flag = 26 to switch from kinematic to penalty formulation to solve the problem. In such cases (Spot_flag = 26) contacts become permissive depending on assigned contact stiffness. It is also recommended to check the contacts quality in animation results to make sure no significant penetrations occur.