RD-E: 1102 Strain Rate Effect
The strain rate effect is considered, and the influence of strain rate filtering studied.
The changes in the mechanical properties at different loading speeds are caused by the increasing speed of the flow stress. As the flow stress increases, the fracture elongation can increase or decrease depending on the material. This also changes the energy a component can absorb in the event of a fast load before failure. In this example, the material strain rate influence with and without filtering will be studied.
Options and Keywords Used
- Shell element
- Isotropic elasto-plastic Johnson-Cook material (/MAT/LAW2 (PLAS_JOHNS))
- Isotropic elasto-plastic material (/MAT/LAW36 (PLAS_TAB))
- Engineering strain/stress, strain rate effect, and filtering
- Boundary conditions (/BCS)
- Imposed velocities (/IMPVEL)
Input Files
The input files used in this example include:
<install_directory>/hwsolvers/demos/radioss/example/11_Tensile_Test/
Model Description
In RD-E: 1101 Elasto-plastic Material Law Characterization, modeling a material’s elasto-plastic behavior based on one material test was looked at. For dynamic problems, the stiffness of a material can depend on the rate of deformation or strain rate. In this example, how to model the stiffness of the material as a function of the strain rate is outlined. First /MAT/LAW2 will be used with two coefficients that scale the stress strain curve depending on the strain rate. Next, test data at different strain rates is used with /MAT/LAW36 to model strain rate behavior of the material. The equivalent strain rate of each element is available as a contour output using the /ANIM/ELEM/EPSD or /H3D/ELEM/EPSD output request.
The strain rate of a tensile test is calculated by dividing the velocity of the gauge region by the gauge length. In this model, the gauge length is measured from node 102 to node 616 and is 80 mm. The displacement and velocity of node 616 is output relative to a moving coordinate (/FRAME/MOV) attached to node 102. Thus, the displacement and velocity of the gauge length can be plotted directly from the relative displacement and velocity of node 616.
Units: mm, ms, kg, N, GPa
Since the time unit is ms, the strain rate unit used in the model is:
/MAT/LAW2
The Johnson-Cook plasticity model (/MAT/LAW2) is used to consider the strain rate effect on the elasto-plastic.
- Strain rate
- Reference strain rate
- Strain rate coefficient
The term scales the stress strain curve for strain rates that are greater than the reference strain rate.
For strain rates less than the reference strain rate, there is no scaling. In this example, there is no test data, so approximate values of = 1x10-4 ms-1 and = 0.05 are used to demonstrate the behavior. When the strain rate behavior of the material is not known, the strain rate coefficient is typically defined as =0 and; thus, there is no strain rate effect for the material.
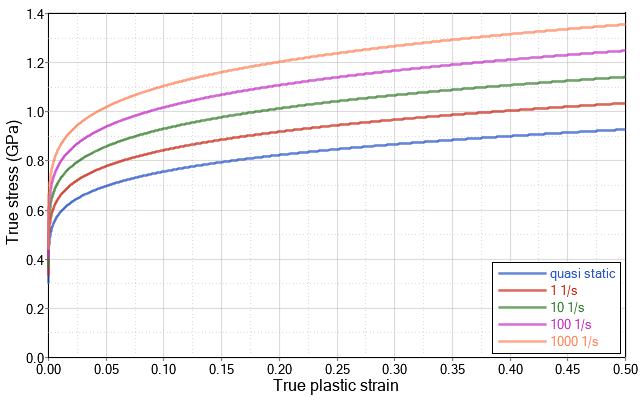
Figure 1. True Stress versus True Plastic Strain at Different Strain Rates for the Johnson-Cook Material Model
/MAT/LAW36
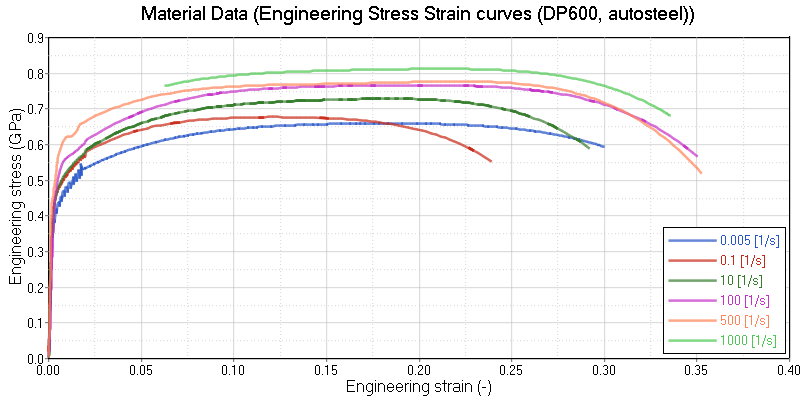
Figure 2. Material Data of Engineering Stress versus Strain for Different Strain Rates. (Steel DP600, original data from autosteel)
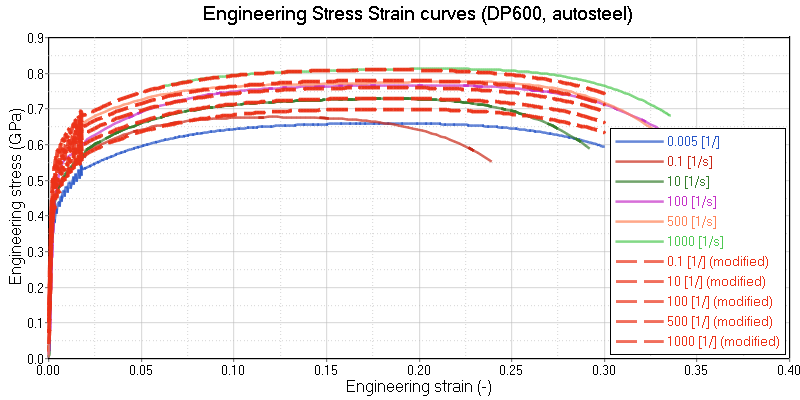
Figure 3. Original and Modified Engineering Stress versus Strain Curves for Different Strain Rates. (Steel DP600, autosteel)
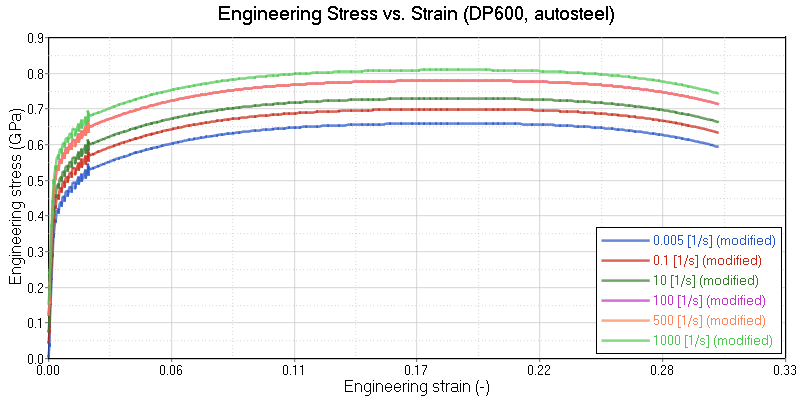
Figure 4. Modified Engineering Stress Strain Curves for Different Strain Rates
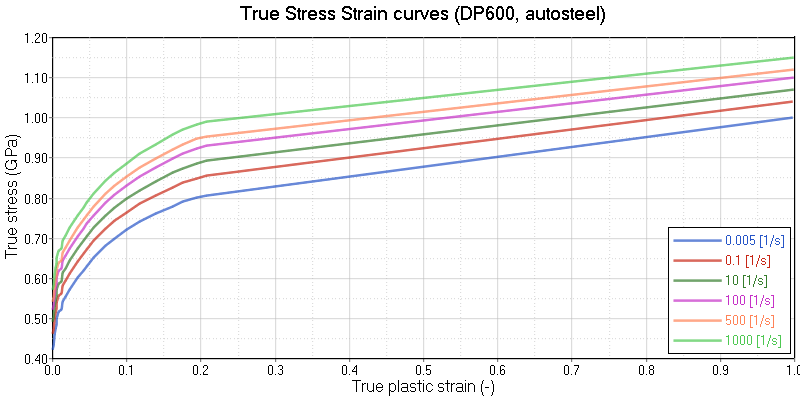
Figure 5. True Stress versus True Plastic Strain Curves for Different Strain Rates
Results
Because of the numerical application of the dynamic loadings, the strain rates are highly oscillating. This can lead to noisy results in the actual and local stress response. To obtain smooth and more physical stress results activate strain rate filtering by setting Fsmooth = 1 and defining a cutoff frequency using Fcut.
- Timestep of the simulation
- Cutoff frequency
- Filtered strain rate
Thus,
The cutoff frequency is a function of the model timestep. Experience shows that the speed of the deformation is important also. For slower speeds like a car crash, 1 – 10 kHz (1000 – 10,000 Hz) is a good value, but for high-speed events, like ballistic, less filtering should be used, so 1 – 10 GHz is appropriate. Good engineering judgment should be used to determine a good value for each simulation.
/MAT/LAW2 with Strain Rate Effect

Figure 6. Comparison of the Distribution of the Strain Rate in the Specimen without Strain Rate Filtering (Fcut=0) . and with strain rate filtering (Fsmooth=1 and Fcut=10 kHz)
The explicit scheme is an element-by-element method and the local treatment of temporal oscillations puts spatial oscillations into the model. A more physical strain rate distribution is achieved by filtering. Moreover, such results show oscillations in the stress strain curve when not damped by filtering.
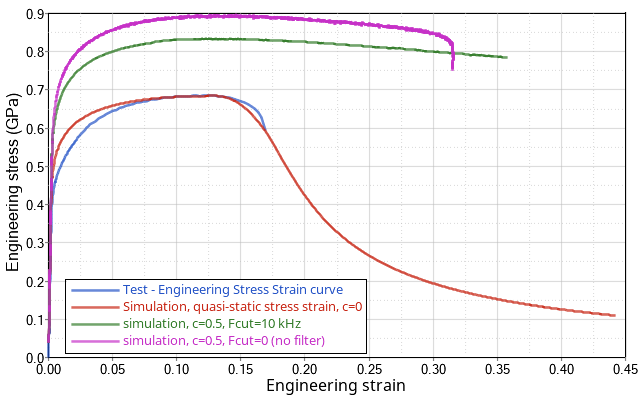
Figure 7. Engineering Stress Strain Curves with and without Strain Rate Filtering /MAT/LAW2
/MAT/LAW36 with Strain Rate Effect

Figure 8. Comparison of the Distribution of the Strain Rate in the Specimen, with and without Strain Rate Filtering /MAT/LAW36
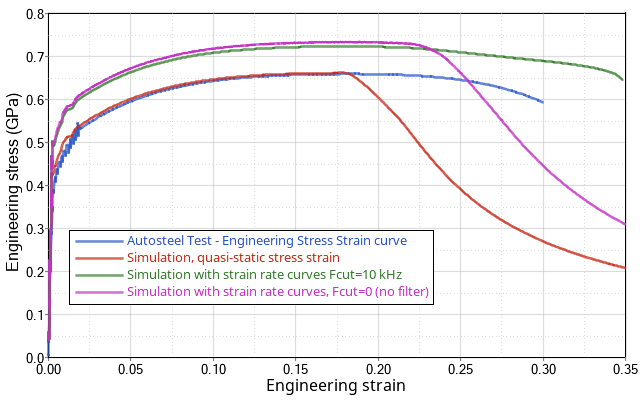
Figure 9. Comparison of the Distribution of the Strain Rate in the Specimen, with and without Strain Rate Filtering (/MAT/LAW36) . and engineering stress strain curves without strain rate
As shown in Figure 9, a strain rate larger than the quasi-static test causes the material to be stiffer. The quasi-static and case without a filter, experience material necking which results in the reduction in stress.
Conclusion
Strain rate effects are important in dynamic events. LAW2 includes 2 parameters that can be used to add strain rate effects to the model. LAW36 allows separate stress versus plastic strain functions to be defined for different strain rates. No matter which material model is used, it is important to use strain rate filtering to reduce numerical noise and smooth the response.