RD-E: 1601 EXPLICIT Solver
A dummy is sat down via gravity using the quasi-static load treatment.
The topic of this study concerns quasi-static load treatment using kinetic relaxation, dynamic relaxation and Rayleigh damping. The explicit solutions provided by the three different approaches will be compared and analyzed.
Options and Keywords Used
- Shell, brick, beam, and dummy
- Quasi-static analysis by explicit, kinetic and dynamic relaxation (/KEREL and /DYREL), and Rayleigh damping (/DAMP)
- Symmetric interface (/INTER/TYPE7)
- Kelvin-Voigt visco-elastic model (/MAT/LAW35 (FOAM_VISC)) and linear elastic law (/MAT/LAW1 (ELAST))
- Added mass (/ADMAS)
- Boundary conditions (/BCS)
- Gravity (/GRAV)
- Material definition (Materials)
- Rigid body (/RBODY)
The goal is to set the body on the seat using a quasi-static approach in order to obtain static equilibrium. The positioning phase is not included in this study. Thus, all nodes of the dummy are placed in a global rigid body in order to maintain the dummy's initial configuration.
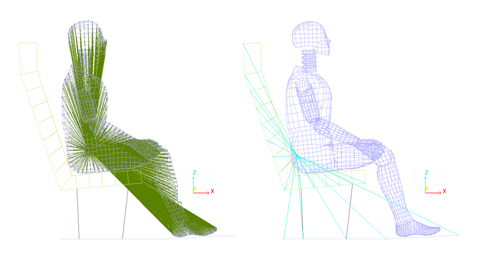
Figure 1. Set up of Both Rigid Bodies
When the ICoG flag is set to 1 for the rigid body of the seat, the center of gravity is computed using the main and secondary node coordinates, and the main node is moved to the center of gravity, where mass and inertia are placed.
When the ICoG flag is set to 3 for the rigid body of the dummy, the center of gravity is set at the main node coordinates defined by you. The added masses and added inertia are transmitted to the main node coordinates.
The main node coordinates and skew are extracted from the pelvis part of the original rigid body.
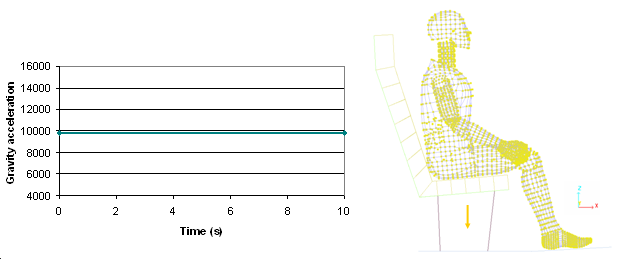
Figure 2. Input Gravity Function (-9810 mm/s-2) and Nodes Selection (yellow)
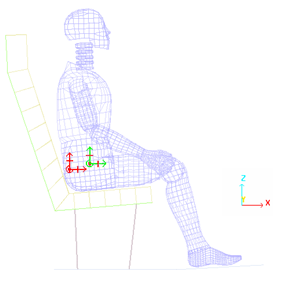
Figure 3. Boundary Conditions on the Rigid Bodies' Main Nodes
Static analysis: quasi-static treatment of gravity loading up to static equilibrium.
The explicit time integration scheme starts with nodal acceleration computation. It is efficient for simulating dynamic loading. However, a quasi-static simulation via a dynamic resolution method needs to minimize the dynamic effects in order to converge towards static equilibrium. This usually describes the pre-loading case prior to dynamic analysis. Thus, the quasi-static solution of gravity loading on the model is the steady-state part of the transient response.
- Kinetic relaxation (/KEREL)
- Dynamic relaxation (/DYREL)
- Rayleigh damping (/DAMP)
Kinetic Relaxation Method
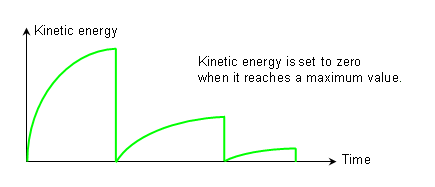
Figure 4. Kinetic Relaxation Method with /KEREL (also named energy discrete relaxation)
Dynamic Relaxation Method
- Relaxation value (recommended default value 1)
- The period to be damped (less than or equal to the highest period of the system)
This option is activated in the Engine file (*_0001.rad) using /DYREL (inputs: and ).
Rayleigh Damping Method
Where, and are the pre-defined constants.
- The th being the damping ratio of the system
- The th being the natural frequency of the system.
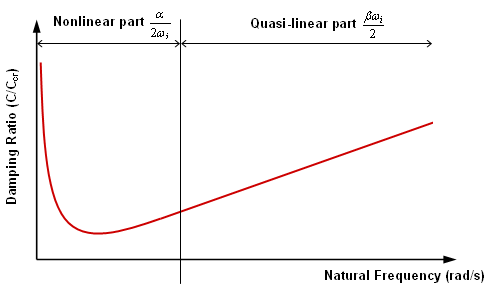
Figure 5. Rayleigh Type Damping
If several frequencies are available, an average of computed values, and may be used.
This model of proportional damping is not recommended for complex structures and does not enable good experimental retiming.
This option is activated in the Engine file (*_0001.rad) using /DAMP (inputs data: and ).
Parameters Used
- First case: = 10 and = 10
- Second case: = 0 and = 10
- Third case: = 10 and = 0
- Fourth case: = 20 and = 0
- First case
- [C] = 10[M] + 10[K]
- Second case
- [C] = 10[K]
- Third case
- [C] = 10[M]
- Fourth case
- [C] = 20[M]
Input Files
- Rayleigh_damping
- <install_directory>/hwsolvers/demos/radioss/example/16_Dummy_Positioning/EXPLICIT_solver/RAYLEIGH/.../SEAT_RAYLEIGH*
- Dynamic_relaxation
- <install_directory>/hwsolvers/demos/radioss/example/16_Dummy_Positioning/EXPLICIT_solver/DYREL/SEAT_DYREL*
- Kinetic_relaxation
- <install_directory>/hwsolvers/demos/radioss/example/16_Dummy_Positioning/EXPLICIT_solver/KEREL/SEAT_KEREL*
- Without_damping
- <install_directory>/hwsolvers/demos/radioss/example/16_Dummy_Positioning/EXPLICIT_solver/Without_damping/SEAT*
Model Description
The purpose is to position a dummy on a foam seat under the gravity field using a quasi-static approach prior to a possible dynamic crash simulation.
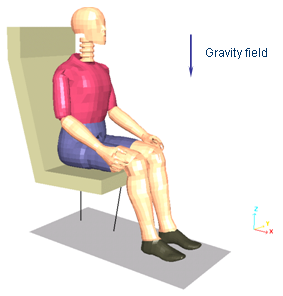
Figure 6. Problem Studied
The dummy weighs 80 kg (173.4 lbs.). The material introduced does not represent the physical case; however, the global weight of the dummy is respected. As the dummy deformation is neglected in this loading phase, simplifying the material characterizations has no incidence on the simulation.
- Material Properties
- Young's modulus
- 210000
- Poisson's ratio
- 0.3
- Density
- 7.8 x 10-9 Gkg/l
- Area
- 2580 mm2
- Inertia
- IXX = 554975 mm4
- Brace thickness
- 2 mm
- Floor thickness
- 1 mm
- Material Properties
- Young's modulus
- 0.2
- Poisson's ratio
- 0
- Density
- 4.3 x 10-11 Gkg/l
- E1 and E2
- 0
- Tangent modulus
- 0.25
- Viscosity in pure shear
- 10000 MPa/s
- C1 = C2 = C3 = 1
- Visco-elastic bulk viscosity
| Compression | -100000 | -10 | 0 | 3000 | 209000 | 210000 |
| Pressure | -1000 | -1000 | 0 | 7.633 | 7.633 | 18.5 |
Visco-elastic Foam Material Law (/MAT/LAW35)
Based on the Navier equation, LAW35 describes materials using visco-elastic behavior. The effect of the air enclosed is taken into account via a separate pressure versus compression function. Relaxation and creep can be modeled.
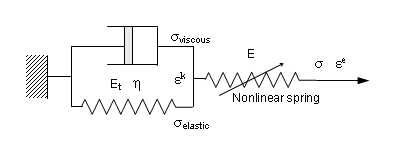
Figure 7. Generalized Kelvin-Voigt Model - LAW35
Refer to the Radioss Theory Manual for explanation of coefficients.
- Density at a time
- Initial density
Model Method
- a dummy composed of 38 parts (limbs and joints).
- a seat comprised of six parts (foam seat back, foam seat cushion, seat back brace, seat bottom brace, seat columns and the floor).
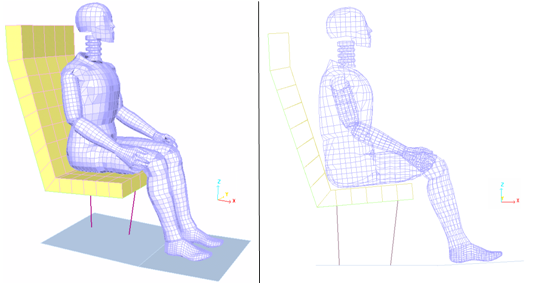
Figure 8. Left: Model Mesh (Perspective view - Shaded display); Right: Model Mesh (Profile view - Edges display)
- Quadratic bulk viscosity
- 1.1
- Linear bulk viscosity
- 0.05
- Hourglass viscosity coefficient
- 0.1
The dummy and seat brace are modeled with shell elements, divided into 4871 4-node shells and 203 3-node shells (Dummy: 5004 shells and seat: 70 shells).
- Shell Properties
- Belytschko hourglass formulation
- Hourglass TYPE4, Ishell = 4
- Membrane hourglass coefficients
- 0.01 (default value)
- Out-of-plane hourglass
- 0.01 (default value)
- Rotation hourglass coefficient
- 0.01 (default value)
- First interface
- Dummy parts
- Secondary nodes
- Seat
- Main surface
- Second interface
- Dummy parts
- Main surface
- Seat
- Secondary nodes
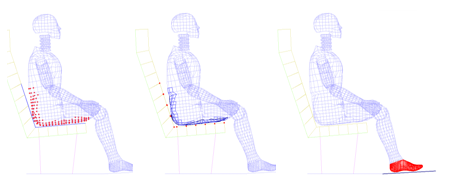
Figure 9. Contacts Modeling with TYPE7 Symmetrical Interface
The gap between the symmetrical interfaces is equal to 5 mm, while a gap of 0.5 mm is set for the other interface.
- Symmetric Interface Properties
- Coulomb friction (Fric flag)
- 0.3
- Critical damping coefficient (Visc flag)
- 0.05
- Scale factor for stiffness (Stfac flag)
- 1
- Sorting factor (Bumult flag)
- 0.20
Refer to the Radioss Theory Manual and Starter Input for further information about the definition of the TYPE7 interface.
Results
Curve and Animation Results Obtained using Kinetic Relaxation: /KEREL
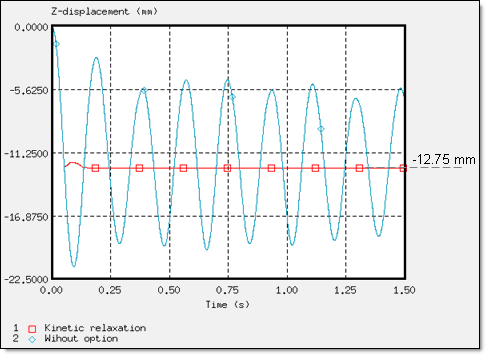
Figure 10. Z-displacement of the Rigid Body's Main Node on Dummy (node 14199)
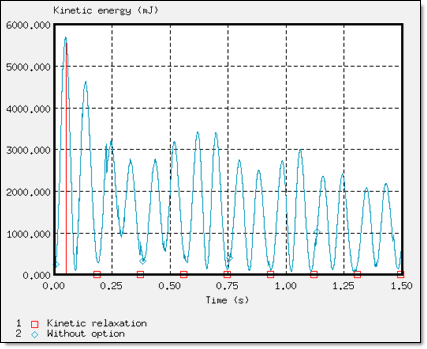
Figure 11. Kinetic Energy of Global Model
Results Obtained using Dynamic Relaxation: /DYREL
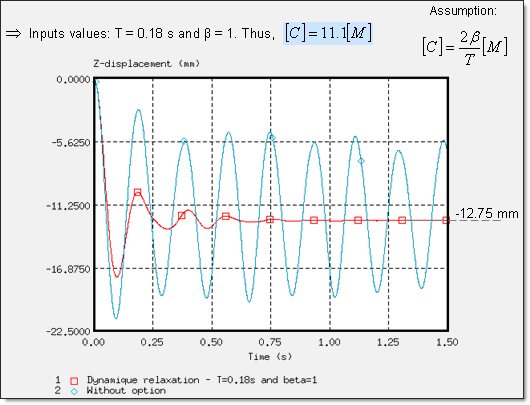
Figure 12. Z-displacement of the Rigid Body's Main Node on Dummy (node 14199)
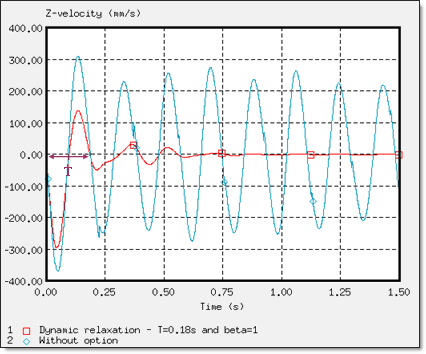
Figure 13. Z-velocity of the Rigid Body's Main Node on Dummy (node 14199)
The period T to be damped is estimated from the velocity curves (highest period).
Results Obtained using Rayleigh Damping: /DAMP
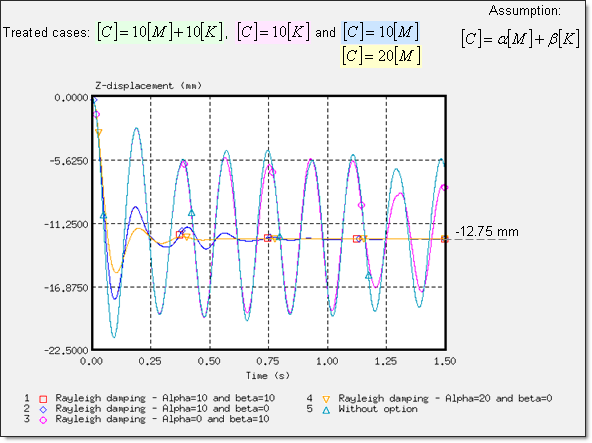
Figure 14. Z-displacement of the Rigid Body's Main Node on Dummy (node 14199)
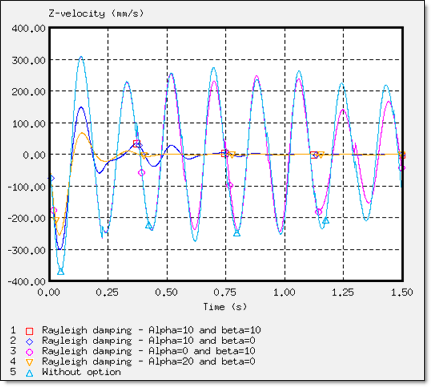
Figure 15. Z-velocity of Rigid Body's Main Node on Dummy (node 14199)
Comparison of the Different Approaches
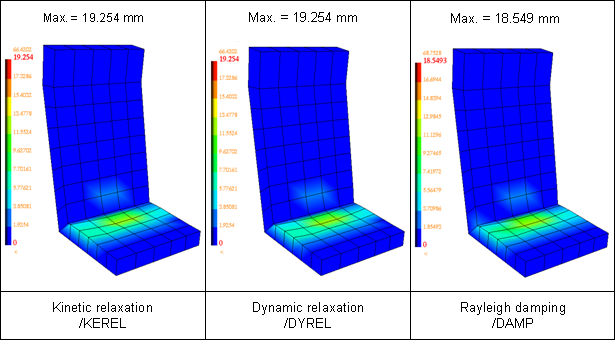
Figure 16. Comparison of the Nodal Displacements' Display on the Seat at Time t = 1.48 s
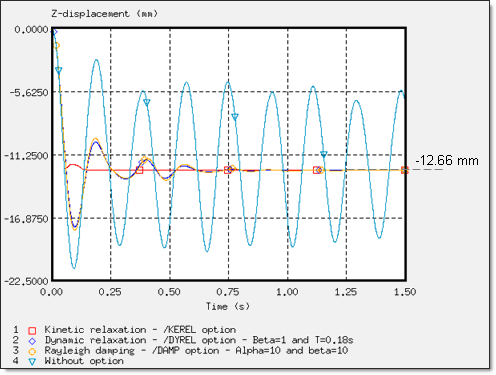
Figure 17. Comparison of Damping on Displacement Obtained using the Three Static Approaches. (Z-displacement of the rigid body's main node on dummy: node 14199)
Conclusion
It is undeniable that the damping methods used to converge towards static equilibrium provide accurate results, especially in the case of this problem where the low rigidity of the seat caused very little quenched oscillations.
The kinetic relaxation introduced in /KEREL, was relatively effective having a swift convergence of the solution towards a static solution, in addition to being easy to use since no input is required. Stability was obtained at 0.137 s.
The /DYREL and /DAMP options are based on viscous damping conducted for the same response, with convergence in three oscillations. Stability was obtained at 0.75 s. Furthermore, dynamic relaxation and the Rayleigh damping methods are basically equivalent in this problem, due to the low stiffness of the seat cushion (Young's modulus is equal to 0.2 ), which breaks the balance between the mass and the weight stiffness in the Rayleigh assumption. Moreover, the boundary conditions and the loading applied on the model lead to a problem described using a predominant natural frequency. Thus, only one parameter, is needed to describe this physical behavior, which reverts back to the dynamic relaxation assumption.
- Dynamic relaxation:
- Rayleigh damping:
10[M]
The approaches available in Radioss provided after convergence a single solution, namely displacement of the dummy by -12.66 mm along the Z-axis and an identical deformation of the seat cushion.