RD-E: 1802 Square Membrane Elastic

This example concerns the in-plane traction-comparison problem of an embedded plate subjected to two concentrated loads, as shown in Figure 2.

This example illustrates the role of the different shell element formulations with regard to the mesh.

Options and Keywords Used

  • Q4 shells
  • T3 shells
  • Hourglass and mesh
  • Boundary conditions (/BCS)

    The boundary conditions are such that the three nodes of a single side and the two middle ones are blocked, whereas the others are free with respect to the Y axis.

  • Concentrated loads (/CLOAD)
    Two concentrated loads are applied on the corner points on opposing sides. They increase over time, as defined by the following function:
    F(t) 0 10 10
    t 0 200 400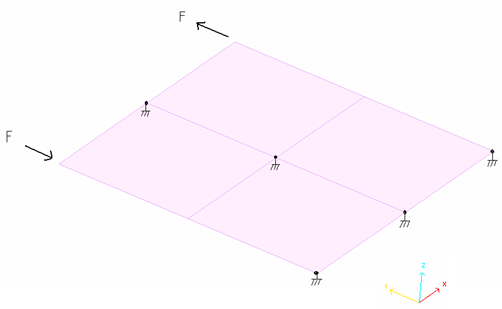

    rad_ex_fig_18-11
    Figure 1. Boundary Conditions and Loads

Input Files

The input files used in this example include:
4Q4
<install_directory>/hwsolvers/demos/radioss/example/18_Square_plate/Membrane_elastic/4Q4/.../TRACTION*
8T3
<install_directory>/hwsolvers/demos/radioss/example/18_Square_plate/Membrane_elastic/8T3/.../TRACTION*
8T3 inv
<install_directory>/hwsolvers/demos/radioss/example/18_Square_plate/Membrane_elastic/8T3_inv/.../TRACTION*
2Q4-4T3
<install_directory>/hwsolvers/demos/radioss/example/18_Square_plate/Membrane_elastic/2Q4-4T3/.../TRACTION*

Model Description

Units: mm, ms, g, N, MPa

The material used follows a linear elastic behavior and has the following characteristics:
Material Properties
Initial density
7.8x10-3 [ g m m 3 ] MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaamWaaeaada WcaaqaaiaadEgaaeaacaWGTbGaamyBamaaCaaaleqabaGaaG4maaaa aaaakiaawUfacaGLDbaaaaa@3BBC@
Young's modulus
210000 [ MPa ] MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWadaqaai Gac2eacaGGqbGaaiyyaaGaay5waiaaw2faaaaa@3BE6@
Poisson ratio
0.3

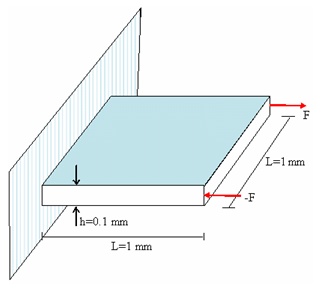
rad_ex_fig_18-9
Figure 2. Geometry of the Problem

Model Method

Four different types of mesh are used:
Mesh 1
Two quadrilateral shells and four triangular shells (2Q4-4T3)
Mesh 2
Four quadrilateral shells (4Q4)
Mesh 3
Eight triangular shells (8T3)
Mesh 4
Eight triangular shells (8T3 inverse)
For each model, the following shell formulations are tested:
  • QBAT formulation (Ishell =12)
  • QEPH formulation (Ishell =24)
  • Belytshcko & Tsay formulation (Ishell =1 or 3, hourglass control TYPE1, TYPE3)
  • C0 and DKT18 formulations

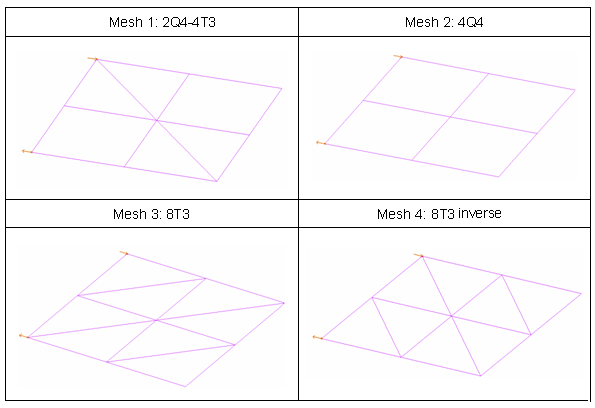
rad_ex_fig_18-18
Figure 3. Square Plate Meshes

Results

Curves and Animations

This example compares several models concerning:
  • the use of different element formulations for each mesh
  • the different types of mesh for a given element formulation
To compare the results, two criteria are used:
  • absorbed energy (internal and hourglass)
  • vertical displacement of the node under the loading point

The following diagrams summarize the results obtained.

Energy Curves / Comparison for Element Formulations

Mesh 1: 2Q4-4T3

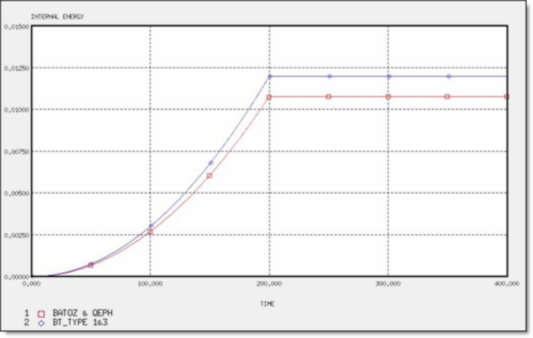
rad_ex_fig_18-12
Figure 4. Internal Energy for 2 x Q4 and 4 x T3 Elements

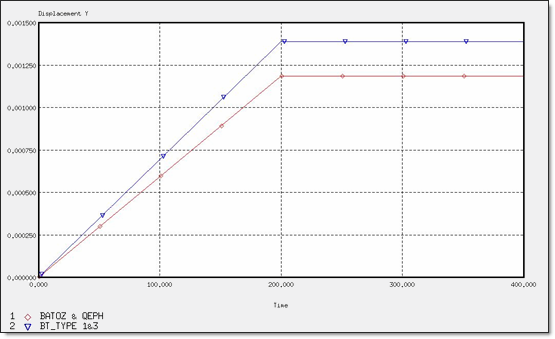
rad_ex_fig_18-13
Figure 5. Y Displacement for 2 x Q4 and 4 x T3 Elements
Mesh 2: 4Q4

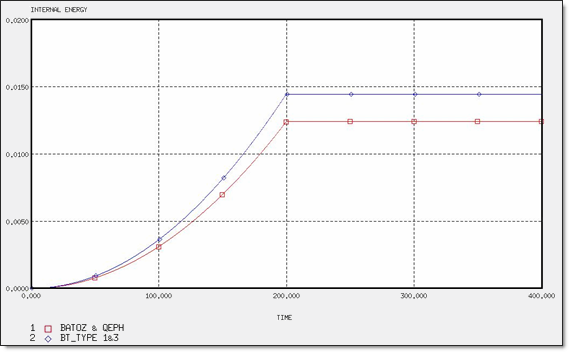
rad_ex_fig_18-14
Figure 6. Internal Energy for 4 x Q4 Elements

Energy Curves / Comparison for Mesh Definitions


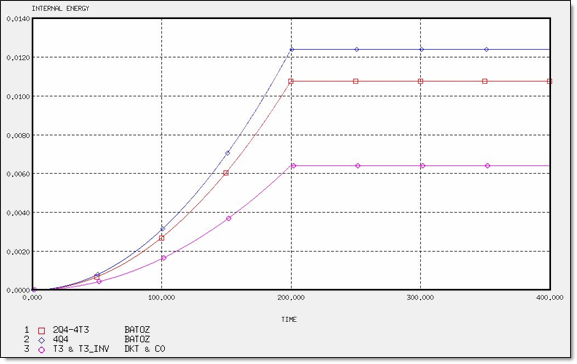
rad_ex_fig_18-15
Figure 7. Internal Energy for Different Meshes

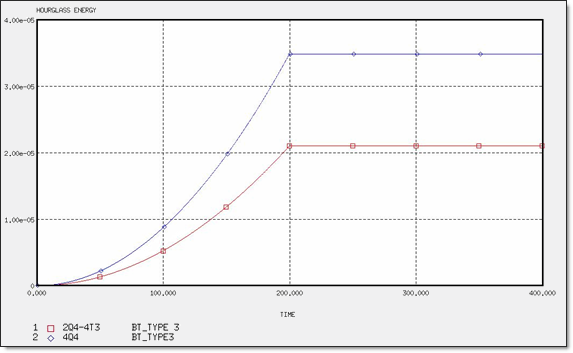
rad_ex_fig_18-16
Figure 8. Hourglass Energy for Different Meshes
Table 1. Displacement and Maximum Energy Comparison
Elastic Plate 2Q4-4T3 4Q4 8T3 8T3_INV
QEPH BT_TYPE 1 and 3 BATOZ QEPH BT_TYPE 1 and 3 BATOZ DKT CO DKT CO
IEmax 1.07 x 10-2 1.19 x 10-2 1.07 x 10-2 1.24 x 10-2 1.44 x 10-2 1.24 x 10-2 6.42 x 10-3 6.42 x 10-3 6.42 x 10-3 6.42 x 10-3
HEmax --- 2.10 x 10-5 -- -- 3.49 x 10-6 -- -- -- -- --
Dymax 1.18 x 10-3 (Traction) 1.38 x 10-3 (Traction) 1.18 x 10-3 (Traction) 1.24 x 10-3 1.44 x 10-3 1.24 x 10-3 6.42 x 10-3 6.42 x 10-3 6.42 x 10-3 6.42 x 10-3

Conclusion

In the case of elastic flat plate modeling, when the loading is in-plane, the shell elements are reduced to become a membrane if the loads applied do not cause buckling.

A general overview of the results obtained highlight the following key points:
  • The quadrilateral shell elements QEPH and QBAT have the same in-plane behavior.
  • The different types of hourglass formulations in the BT shell elements lead to the same results, as there is no out-of-plane deformation and the material is supposed to be elastic.
  • The three in-plane behaviors of the DKT18 and T3C0 Radioss triangles are exactly the same, as both of the elements are used for the same membrane formulation.
  • The triangles are stiffer than the quadrilateral elements and do not provide good results, especially when the mesh is coarse.

Refer to the Radioss Theory Manual for more details.