RD-E: 1702 Transitions
A steel box beam, fixed at one end, impacted at the other end by an infinite mass. Results for meshes with different transitions are compared.
The dimensions of the box beam are 203 mm x 50.8 mm x 38.1 mm, and its thickness is 0.914 mm. As symmetry is taken into account, only one quarter of the structure is modeled. Four kinds of mesh and three plasticity formulations are compared (global plasticity, five integration points and iterative plasticity).
Options and Keywords Used
- Q4 shells
- Interfaces (/INTER/TYPE7 and /INTER/TYPE11)
The structure's self-impact is modeled using a TYPE7 interface on the full structure. The interface main surface is defined using the complete model. The secondary nodes group is defined using the main surface.
On top of the beam, the possible edge-to-edge impacts are dealt with using a TYPE11 self-impacting interface. The edges use the main surface of the TYPE 7 interface as the input surface.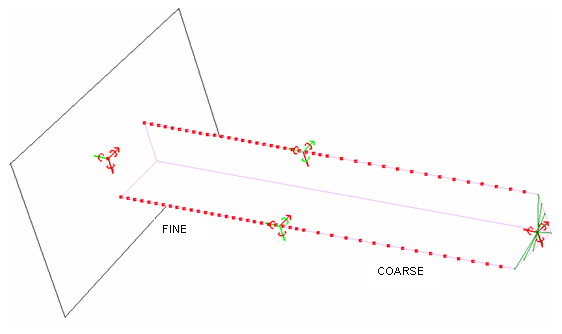
Figure 1. Boundary Conditions - Global plasticity, iterative plasticity, and variable thickness
- BT_TYPE1-3-4, QEPH, BATOZ, DKT18 and C0 formulation
- Boundary conditions (/BCS)
Take into account the symmetry, all nodes in the Y-Z plan are fixed in a Y translation and an X and Z rotation. One quarter of the structure is modeled.
- Rigid wall (/RWALL)
The impactor is modeled by a sliding rigid wall using a fixed velocity (13.3 m/s) in the Z-direction and fixed for other translations and rotations.
- Imposed velocity (/IMPVEL)
- Rigid body (/RBODY)
The lower (fixed) end is modeled using a rigid body connecting all lower nodes (Z = 0.0). The rigid body is completely fixed in translations and rotations.
Input Files
- Mesh 0
- <install_directory>/hwsolvers/demos/radioss/example/17_BoxBeam/Transition_mesh/mesh0/.../BOXBEAM*
- Mesh 1
- <install_directory>/hwsolvers/demos/radioss/example/17_BoxBeam/Transition_mesh/mesh1/.../BOXBEAM*
- Mesh 2
- <install_directory>/hwsolvers/demos/radioss/example/17_BoxBeam/Transition_mesh/mesh2/.../BOXBEAM*
- Mesh 3
- <install_directory>/hwsolvers/demos/radioss/example/17_BoxBeam/Transition_mesh/mesh3/.../BOXBEAM*
Model Description
Units: mm, ms, g, N, MPa
- Material Properties
- Initial density
- 7.8 x 10-3
- Young's modulus
- 210000
- Poisson ratio
- 0.3
- Yield stress
- 206
- Hardening parameter
- 450
- Hardening exponent
- 0.5
- Maximum stress
- 340
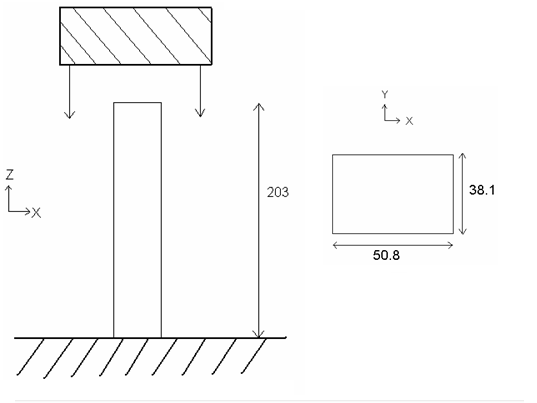
Figure 2. Problem Studied
Model Method
The layout of the elements is shown in Figure 3.
- Element formulation:
- BT_TYPE1
- BT_TYPE3
- QEPH
- BATOZ
- C0
- DKT18
- Plasticity:
- Global plasticity
- Progressive plasticity with five integration points
- Iterative plasticity with five integration points and variable thickness
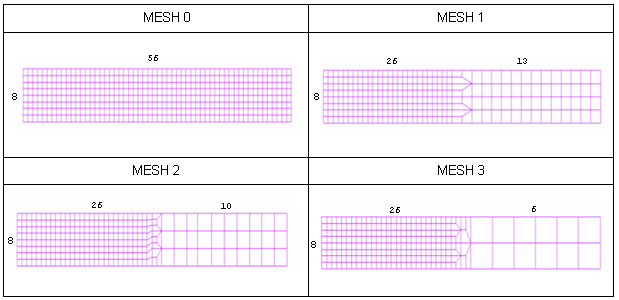
Figure 3. Meshes
Results
- Role and influence of the mesh for a given type of element formulation
- Shell element formulations for a given mesh
- Plasticity options for a given mesh and element formulation
- Crushing force versus displacement
The crushing force corresponds to the normal force in the Z-direction of the impactor (rigid wall), multiplied by 4 due to symmetry.
For comparison, displacement corresponds to the Z-direction motion of the rigid wall's main node.
- Hourglass energy
- Total energy
Total energy is the sum of all energies.
Mesh Influence for a Given Shell Using Global Plasticity
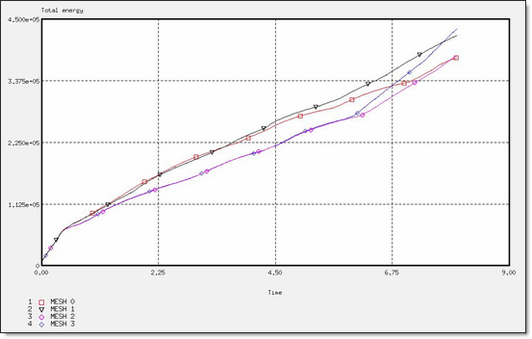
Figure 4. Total Energy for a BATOZ Formulation
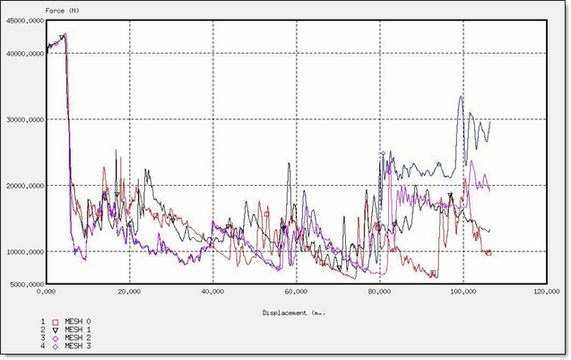
Figure 5. Force for a BATOZ Formulation
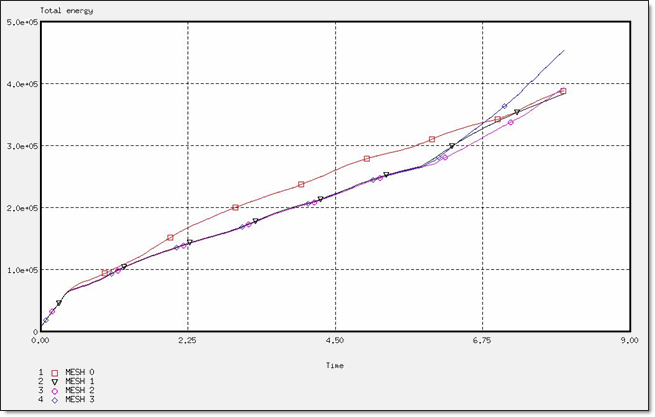
Figure 6. Total Energy for a QEPH Formulation
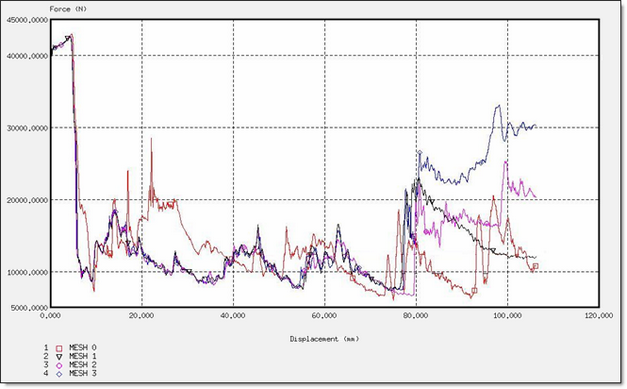
Figure 7. Force for a QEPH Formulation
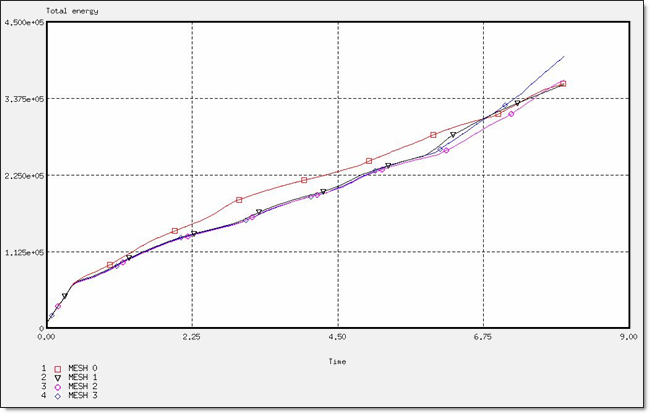
Figure 8. Total Energy for a BT_TYPE1 Formulation
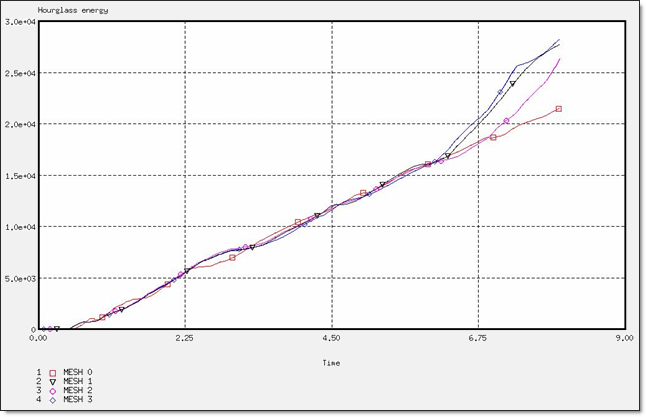
Figure 9. Hourglass Energy for a BT_TYPE1 Formulation
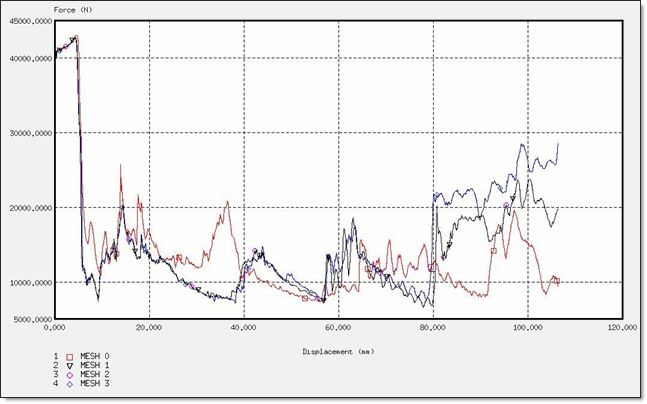
Figure 10. Force for a BT_TYPE1 Formulation
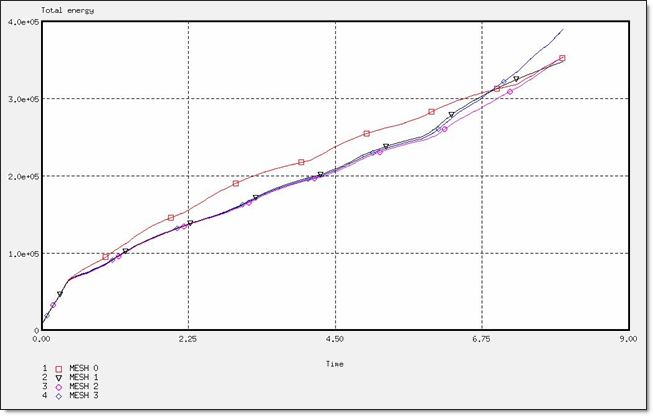
Figure 11. Total Energy for a BT_TYPE3 Formulation
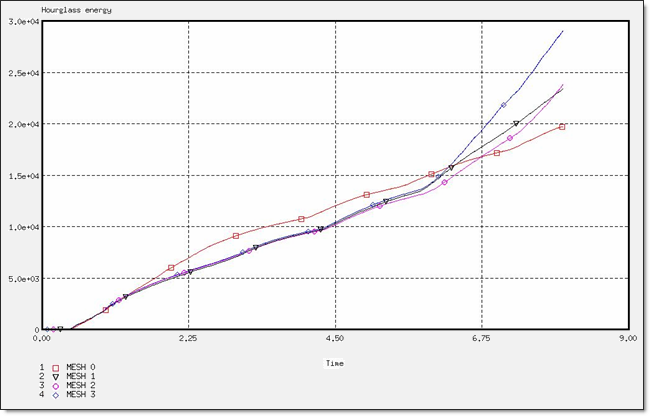
Figure 12. Hourglass Energy for a BT_TYPE3 Formulation
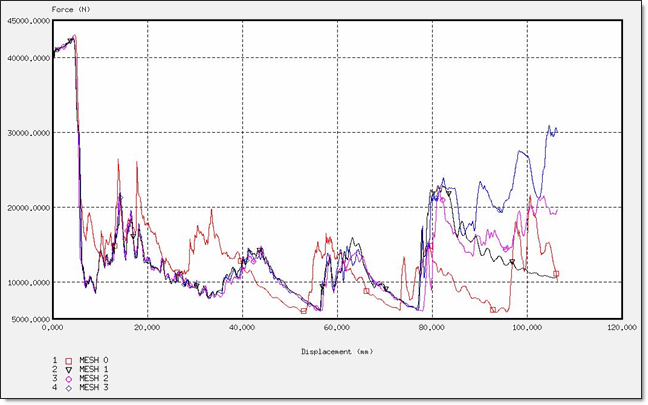
Figure 13. Force for a BT_TYPE3 Formulation
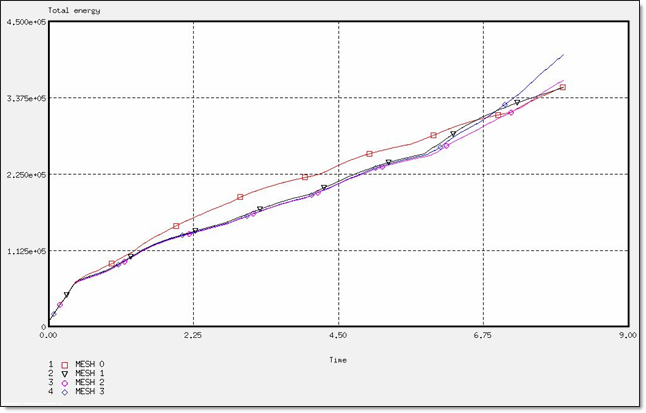
Figure 14. Total Energy for a BT_TYPE4 Formulation
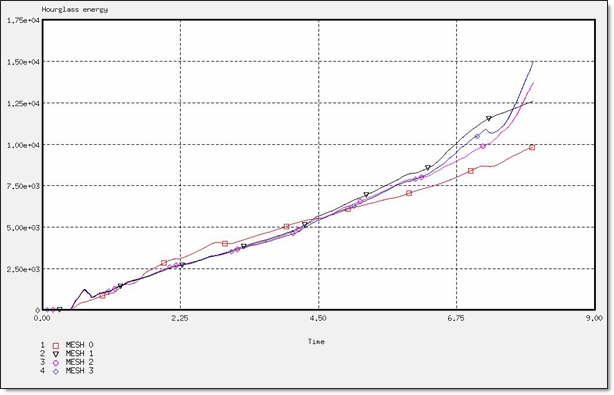
Figure 15. Hourglass Energy for a BT_TYPE4 Formulation
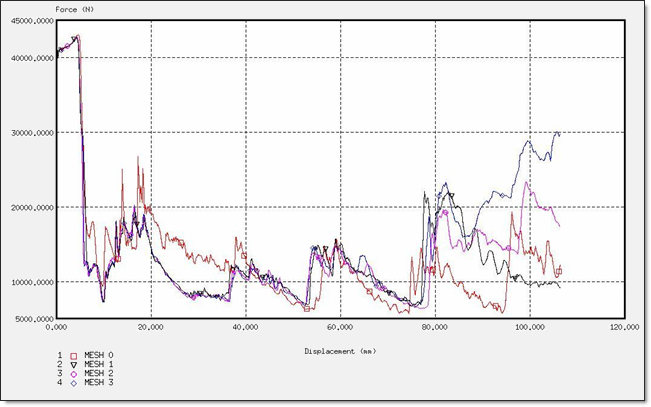
Figure 16. Force for a BT_TYPE4 Formulation
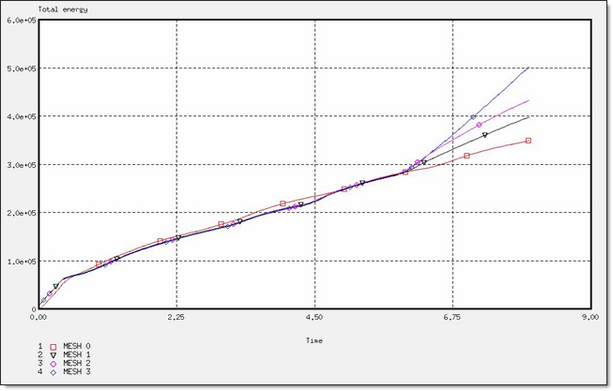
Figure 17. Total Energy for a CO Formulation
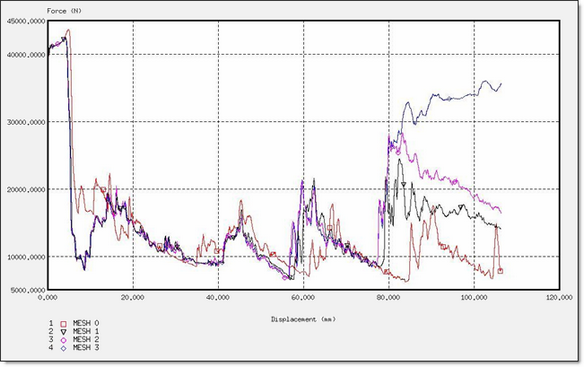
Figure 18. Force for a CO Formulation
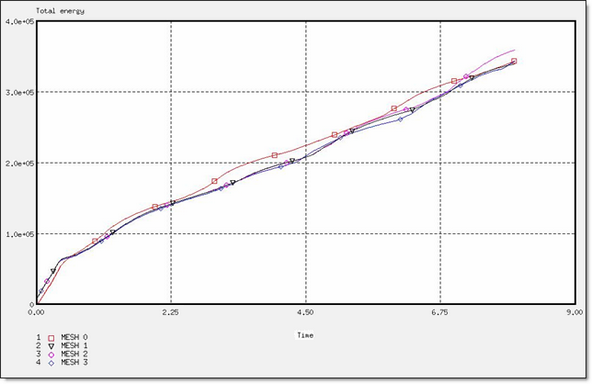
Figure 19. Total Energy for a DKT Formulation
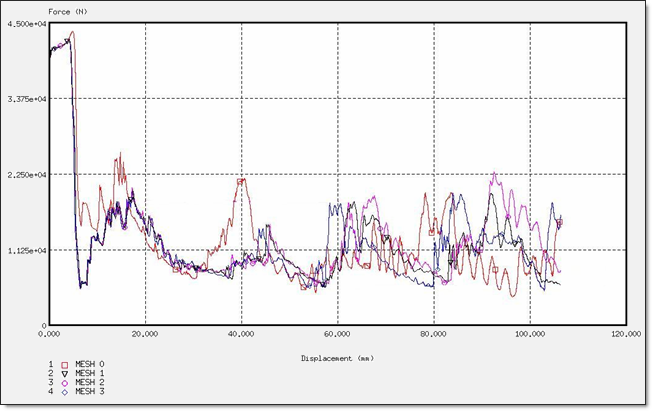
Figure 20. Force for a DKT Formulation
Influence of Element Formulation Using Mesh 3 and Global Plasticity
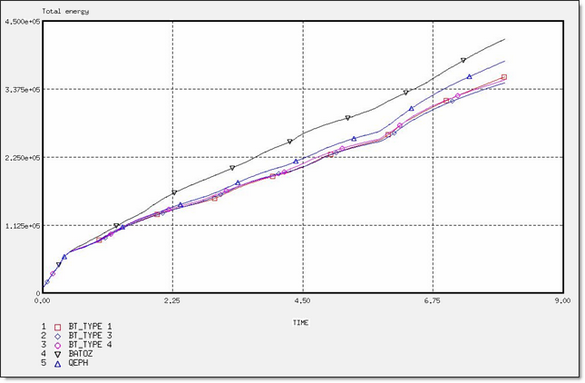
Figure 21. Total Energy for Different Element Formulations
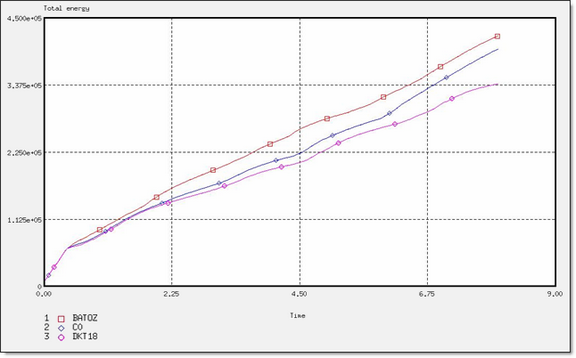
Figure 22. Total Energy for Different Element Formulations
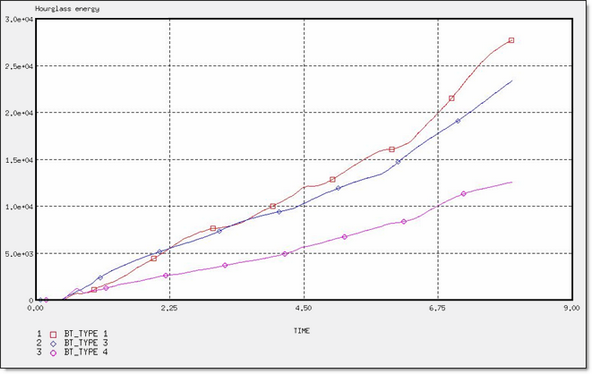
Figure 23. Hourglass Energy for Different Element Formulations
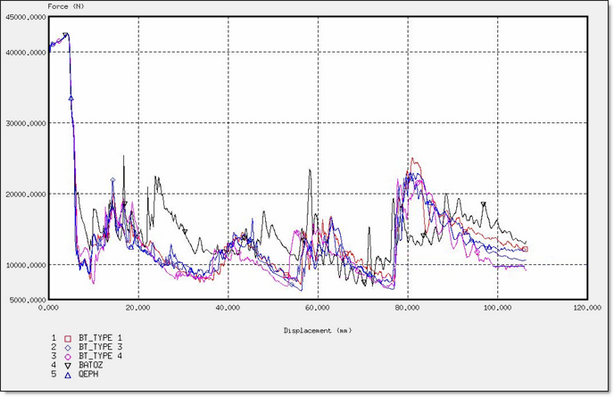
Figure 24. Force for Different Element Formulations
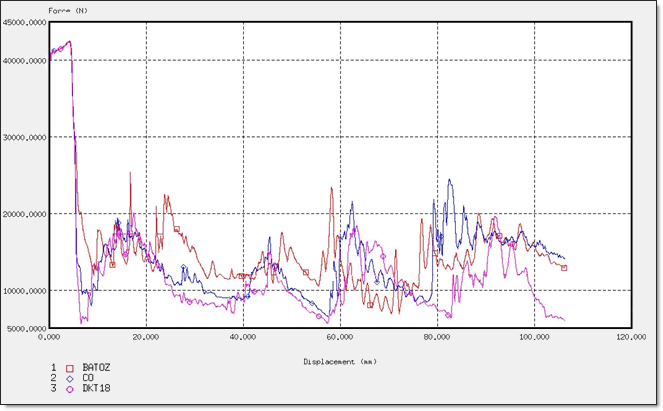
Figure 25. Displacements for Different Element Formulations
Influence of Plasticity Options Using Mesh 1 and BT_TYPE3 Formulation
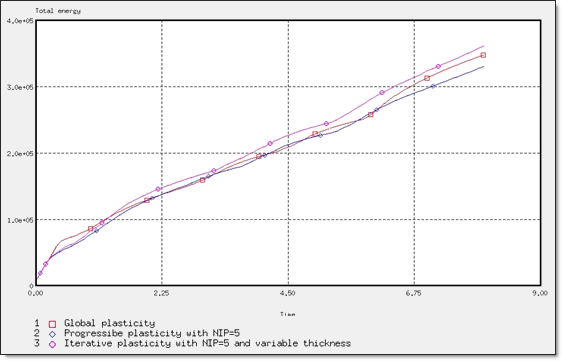
Figure 26. Total Energy for Different Plasticity Computations
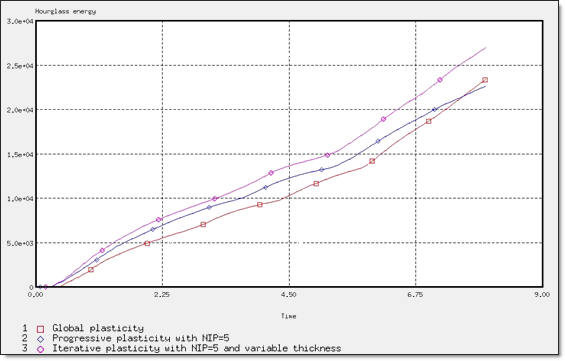
Figure 27. Hourglass Energy for Different Plasticity Computations
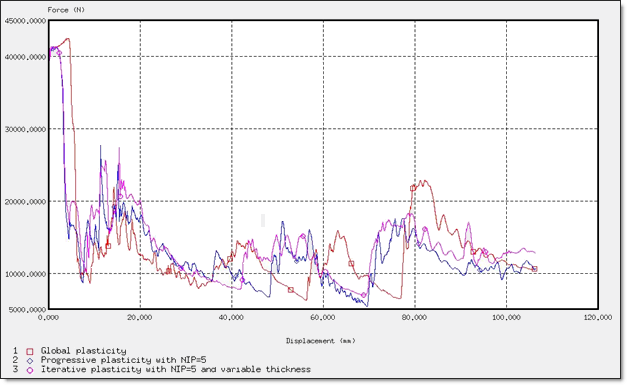
Figure 28. Force for Different Plasticity Computations
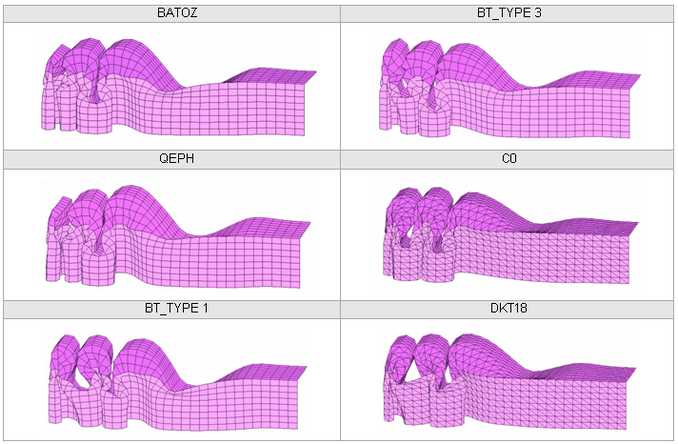
Figure 29. MESH 0
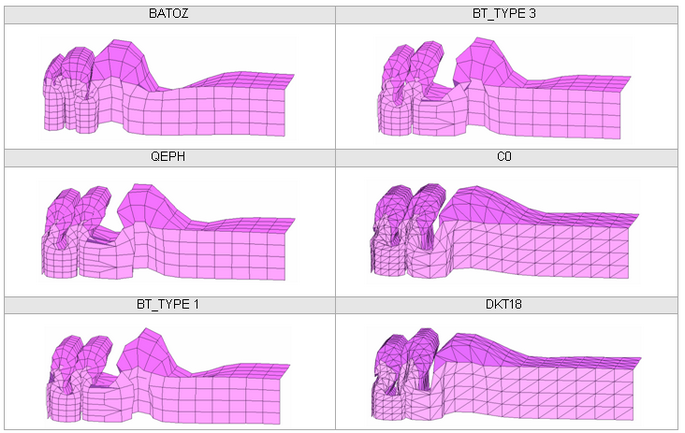
Figure 30. MESH 1
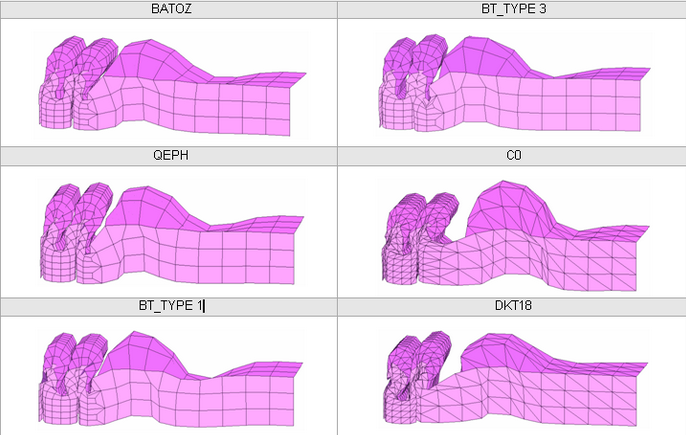
Figure 31. MESH 2
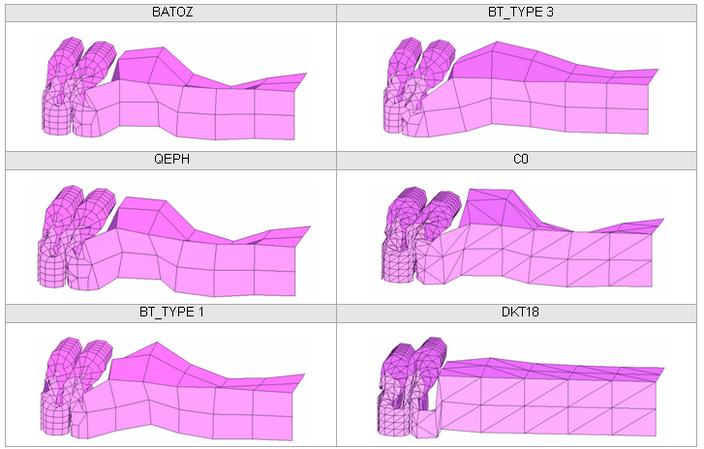
Figure 32. MESH 3
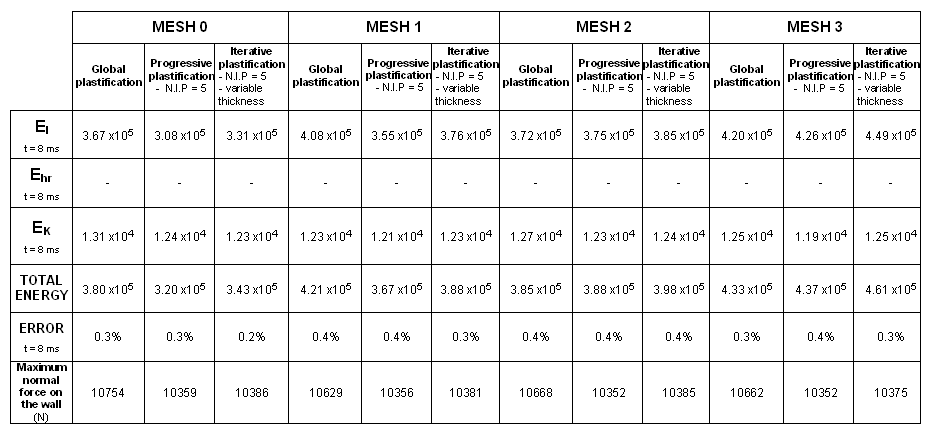
Figure 33.
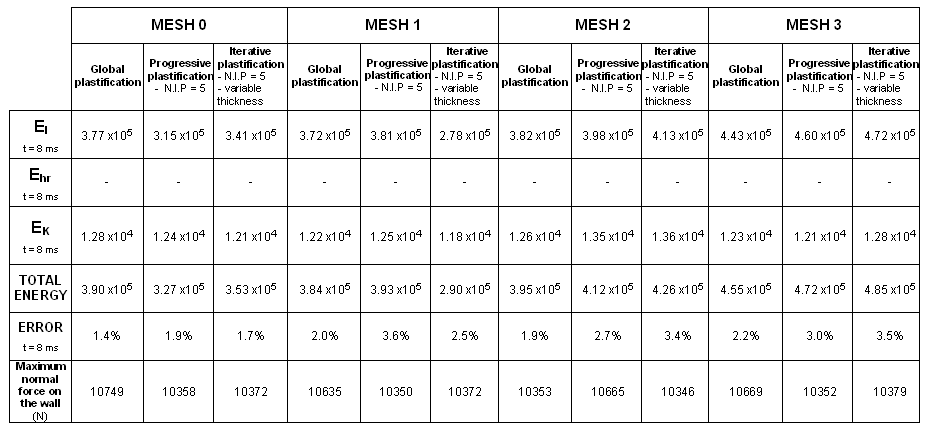
Figure 34. Formulation: QEPH
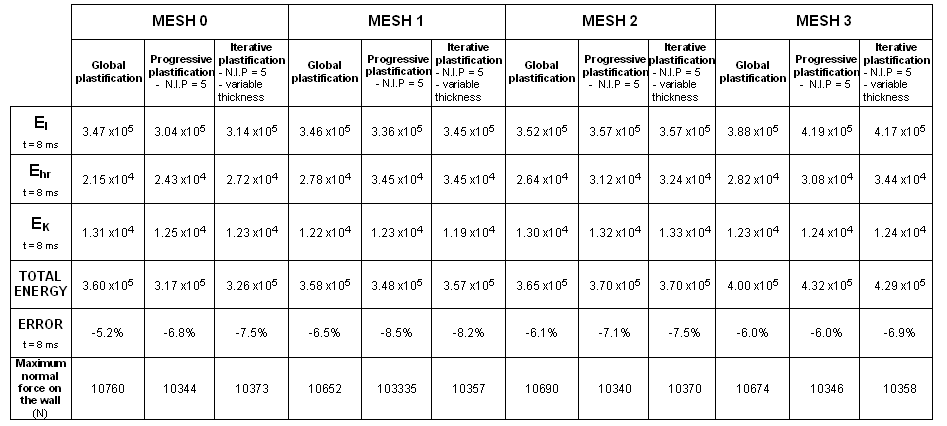
Figure 35. Formulation: BT_TYPE1
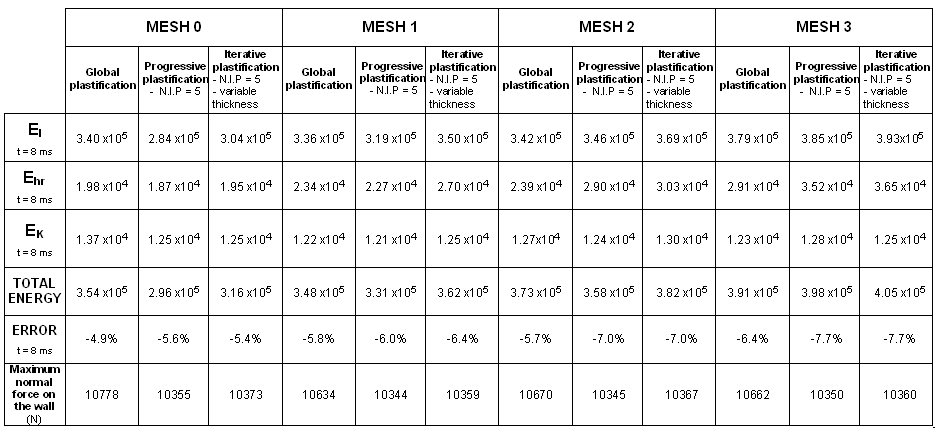
Figure 36. Formulation: BT_TYPE3
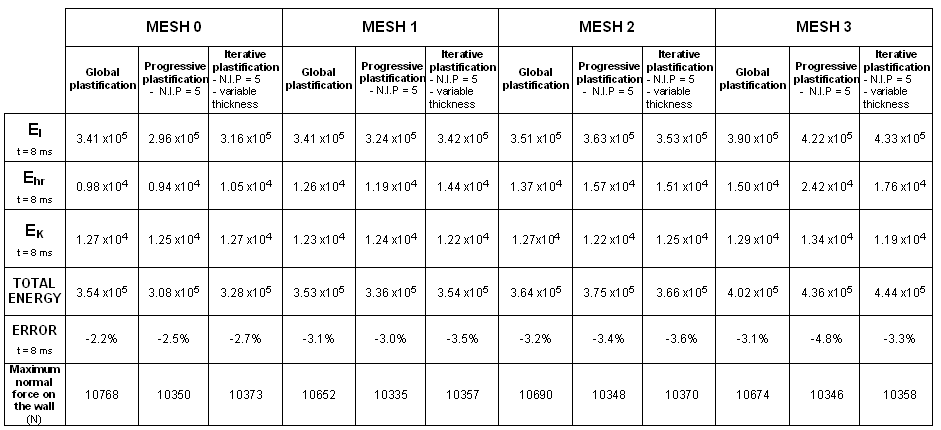
Figure 37. Formulation: BT_TYPE4
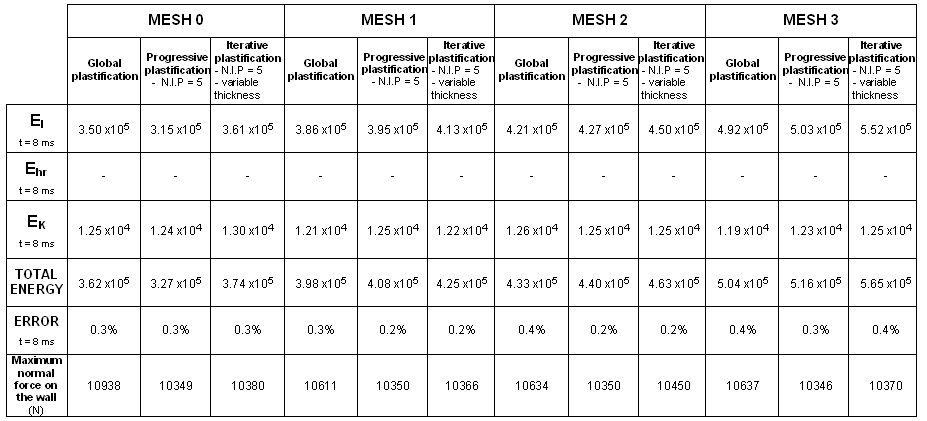
Figure 38. Formulation: C0
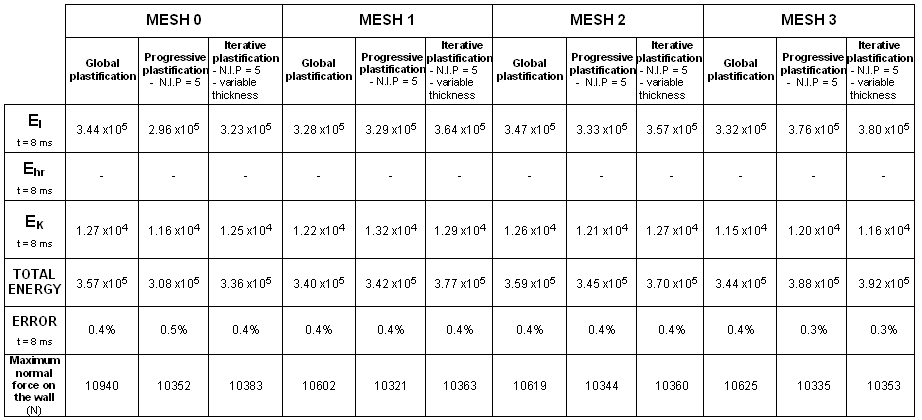
Figure 39. Formulation: DKT18
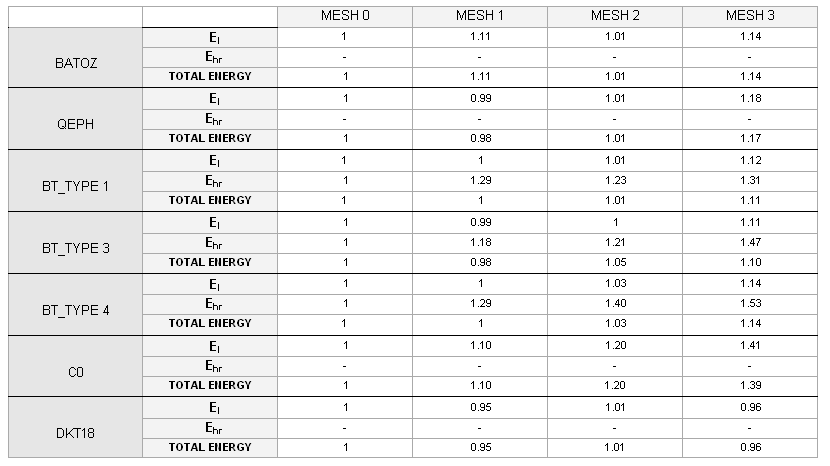
Figure 40.
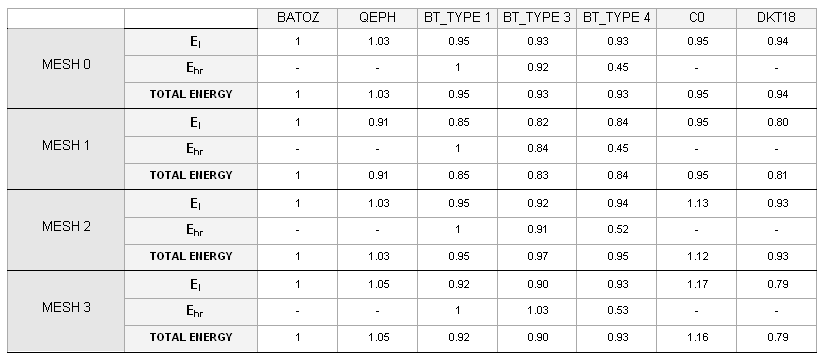
Figure 41.