/PROP/TYPE8 (SPR_GENE)

Deformation, force and energy based failure criteria are available. The general spring property is often used to model a joint connection between two parts.

Format

Definitions

Comments

1. The spring has six DOF computed in a skew system frame: ${\delta }_{{\mathbf{X}}^{\prime }},{\delta }_{{\mathbf{Y}}^{\prime }},{\delta }_{{\mathbf{Z}}^{\prime }},{\theta }_{{\mathbf{X}}^{\prime }},{\theta }_{{\mathbf{Y}}^{\prime }},{\theta }_{{\mathbf{Z}}^{\prime }}$

   
   
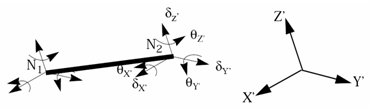
   Figure 1.

   • The six DOF are independent. If initial length is not equal to zero, the equilibrium is insured for forces, but not for moments. It is then recommended to use spring elements TYPE8 with a zero length or with one of the two nodes fixed in all directions.
   • If $\delta$ is a translational DOF, the force in direction $\delta$ is computed as:

     Linear spring:

     $\text{F}(\delta )=K_i{\delta }^i+C_i{\dot{\delta }}^i$ for $i$ = 1, 2, 3

     Nonlinear spring:

     $\text{F}(\delta )=\text{f}\left(\frac{{\delta }^i}{{\mathit{Ascale}}_i}\right)\left[A_i+B_i\text{ln}\left|\frac{{\dot{\delta }}^i}{D_i}\right|+E_i\text{g}\left(\frac{{\dot{\delta }}^i}{F_i}\right)\right]+C_i{\dot{\delta }}^i+{\mathit{Hscale}}_i\text{h}\left(\frac{{\dot{\delta }}^i}{F_i}\right)$ for i= 1, 2, 3

   • If $\theta$ is a rotational DOF, the moment is computed as:

     Linear spring:

     $\text{M}(\theta )=K_i{\theta }^i+C_i{\dot{\theta }}^i$ for $i$ = 4, 5, 6

     Nonlinear spring:

     $\text{M}(\theta )=\text{f}\left(\frac{{\theta }^i}{{\mathit{Ascale}}_i}\right)\left[A_i+B_i\text{ln}\left|\frac{{\dot{\theta }}^i}{D_i}\right|+E_i\text{g}\left(\frac{{\dot{\theta }}^i}{F_i}\right)\right]+C_i{\dot{\theta }}^i+{\mathit{Hscale}}_i\text{h}\left(\frac{{\dot{\theta }}^i}{F_i}\right)$ for $i$ = 4, 5, 6

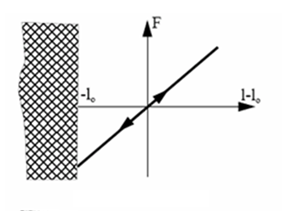
     Figure 2. Linear Spring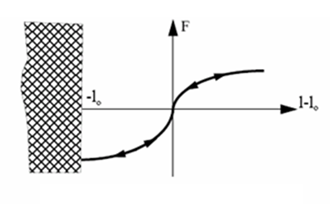	Figure 3. Nonlinear Elastic Spring, Hi=0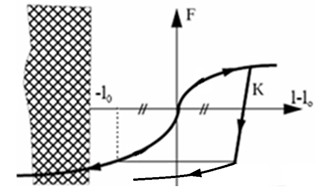
     Figure 4. Nonlinear Elastic Plastic Spring, Hi=1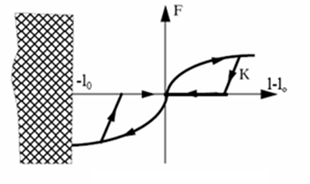	Figure 5. Nonlinear Elasto- plastic Spring with Decoupled Hardening in Tension and Compression, Hi= 2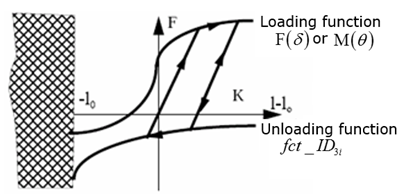
     Figure 6. Nonlinear Elastic Plastic Spring "kinematic" Hardening, Hi= 4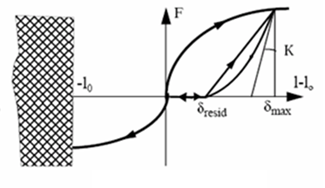	Figure 7. Nonlinear Elastic Plastic Spring "kinematic" Hardening, Hi= 5
     Figure 8. Nonlinear Elasto-Plastic Spring with Isotropic Hardening and Nonlinear Unloading, Hi= 6	Figure 9. Nonlinear Spring with Elastic Hysteresis, Hi=7

     With $i$ =1, 2, 3, 4, 5, 6

2. If I_equil = 0, then:(1)
   $$\text{f}\left(\theta \right)=M_{2y}=-M_{1y}$$

   $M_{2y}$ is moment in $Y$ by N₂

   $M_{1y}$ is moment in $Y$ by N₁

3. If I_equil = 1, then:(2)
   $$-M_{1y}\ne M_{2y}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-M_{1z}\ne M_{2z}$$
   (3)
   $$\text{f}\left(\theta \right)=\frac{M_{2y}-M_{1y}}{2}$$

   $M_{2y}$ is moment in $Y$ by N₂

   $M_{1y}$ is moment in $Y$ by N₁

   $M_{2z}$ is moment in $Z$ by N₂

   $M_{1z}$ is moment in $Z$ by N₁

4. Failure criterion:
   • If the failure criterion is uni-directional, I_fail=0, the spring fails as soon as one of the criteria is met in one direction.

     $\frac{{\delta }^i}{{\delta }_{\max }^i}\ge 1$ or $\left|\frac{{\delta }^i}{{\delta }_{\min }^i}\right|\ge 1$ with ${\delta }_{\text{max}}^{\mathrm{i}}$ and ${\delta }_{\text{min}}^{\mathrm{i}}$ being the failure limits in direction $i$ =1,2,3

     $\frac{{\theta }^i}{{\theta }_{\max }^i}\ge 1$ or $\left|\frac{{\theta }^i}{{\theta }_{\min }^i}\right|\ge 1$ with ${\theta }_{\text{max}}^i$ and ${\theta }_{\text{min}}^i$ being the failure limits in direction $i$ =4,5,6

   • If the failure criteria is multi-directional, I_fail=1, the spring fails if the following criteria is fulfilled:(4)
     $${{\displaystyle \sum _{i=1,2,3}\left(\frac{{\delta }^i}{{\delta }_{fail}^i}\right)}}^2+{{\displaystyle \sum _{i=4,5,6}\left(\frac{{\theta }_{in}^i}{{\theta }_{fail}^i}\right)}}^2\ge 1$$

     with ${\delta }_{\mathit{fail}}^i$ being the failure displacement in direction $i$ = 1, 2, 3; and ${\theta }_{fail}^i$ being the falure displacement (rotation) in direction $i$ =4,5,6.

   • If ${\delta }_{\text{min}}^i$ (resp ${\delta }_{\text{max}}^i$ , with $i$ =1, 2, 3) is 0, no failure in the negative direction (resp positive).
   • The failure model flag I_fail2 allows the 3 types of failure criteria:
     1. If I_fail2= 0, the displacemenet/rotation criterion is activated:(5)
        $${\delta }_{fail}^i=\{\begin{array}{c}{\delta }_{\max }^i,if\left({\delta }^i>0\right)\\ {\delta }_{\min }^i,if\left({\delta }^i\le 0\right)\end{array}$$
        Where, ${\delta }_{\text{min}}^i$ and ${\delta }_{\text{max}}^i$ are the static failure limit in translational DOF.(6)

        $${\theta }_{fail}^i=\{\begin{array}{c}{\theta }_{\max }^i,if\left({\theta }^i>0\right)\\ {\theta }_{\min }^i,if\left({\theta }^i\le 0\right)\end{array}$$

        Where, ${\theta }_{\text{min}}^i$ and ${\theta }_{\text{max}}^i$ are the static failure limit in rotational DOF.

     2. If I_fail2=1, the force/moment criterion is activated:(7)
        $${\delta }_{fail}^i=\{\begin{array}{c}{\delta }_{\max }^i,if\left({\delta }^i>0\right)\\ {\delta }_{\min }^i,if\left({\delta }^i\le 0\right)\end{array}$$
        Where, ${\delta }_{\text{min}}^i$ and ${\delta }_{\text{max}}^i$ are the static force failure limit in translational DOF.(8)

        $${\theta }_{fail}^i=\{\begin{array}{c}{\theta }_{\max }^i,if\left({\theta }^i>0\right)\\ {\theta }_{\min }^i,if\left({\theta }^i\le 0\right)\end{array}$$

        Where, ${\theta }_{\text{min}}^i$ and ${\theta }_{\text{max}}^i$ are the static moment failure limit in rotational DOF.

        In this case, the displacement/rotation values are replaced by failure force/moment values.

     3. If I_fail2=3, the energey criterion is activated:(9)
        $${\delta }_{fail}^i={\delta }_{\max }^i$$
        Where, ${\delta }_{\text{max}}^i$ is the static energy failure limit in translational DOF.(10)

        $${\theta }_{fail}^i={\theta }_{\max }^i$$

        Where, ${\theta }_{\text{max}}^i$ is the static energy falure limit in rotational DOF.

        In this case, the displacement/rotation values are replaced by positive failure energy values.

5. For each direction, ${\delta }_{\text{min}}^i$ (with $i$ =1, 2, 3) is taken if $\delta$ ⁱ is negative, otherwise, ${\delta }_{\text{max}}^i$ is taken if is positive. The ${\delta }_{\text{min}}^i$ (with $i$ =1, 2, 3) must be negative. Both ${\theta }_{\text{min}}^i$ (with $i$ =4, 5, 6) and ${\theta }_{\text{max}}^i$ are expressed in radians.
6. If K_i (with $i$ =1, 2, 3) is less than the maximum slope of the yield curve (K_i is not consistent with the maximum slope of yield curve), K_i is set to the maximum slope of the curve.

   If K_i (with i=4, 5, 6) is less than the maximum slope of the yield curve (K_i is not consistent with the maximum slope of yield curve), K_i is set to the maximum slope of the curve.

7. If hardening flag H_i is 4, the loading curve should be positive for all values of abscissa. The unloading curve in this case should be negative for all values of abscissa. For flag 4, these curves represents upper and lower limits of yield force as function of current spring length variation or strain. The force jumps between the curves each time when the direction of deformation changes.
8. If hardening flag H_i is 5, residual deformation is a function of maximum displacement:

   ${\delta }_{\mathit{resid}}={\text{f}}_{N3}\left({\delta }_{\text{max}}^i\right)$ with $i$ =1, 2, 3

   ${\theta }_{\mathit{resid}}={\text{f}}_{N3}\left({\theta }_{\text{max}}^i\right)$ with $i$ =4, 5, 6

9. For linear springs, $\mathrm{f}\left(\delta \right)$ and $\text{g}\left(\dot{\delta }\right)$ (or $\mathrm{f}\left(\theta \right)$ and $\text{g}\left(\dot{\theta }\right)$ ) are null functions and A_i, B_i, and E_i, are not taken into account.
10. The third node in element definition is not used to determine local coordinate system of the spring. The local coordinate system is determined either by setting a skew or by using global coordinate system, when the skew is not given.
11. Spring is in compression in a given direction of local coordinate system, when projection of direction from initial position of node N1 to current position of node N1 to the direction of the local coordinate system is positive. Otherwise, the spring is in tension in corresponding direction of local coordinate system.
12. Spring is activated and/or deactivated by sensor:
    • If sens_ID ≠ 0 and I_sflag = 0, the spring element is activated by the sens_ID.
    • If sens_ID ≠ 0 and I_sflag = 1, the spring element is deactivated by the sens_ID.
    • If sens_ID $\ne$ 0 and I_sflag = 2, then:
      • The spring is activated and, or, deactivated by sensor sens_ID (if sensor is ON, spring is ON; if sensor is OFF, spring is OFF)
      • The spring reference length ( $l_0$ ) is the distance between node N1 and N2 at the time of sensor activation.

    If a sensor is used for activating or deactivating a spring, the reference length of the spring at sensor activation (or deactivation) is equal to the nodal distance at time = 0; except if sensor flag is equal to 2.