/PROP/TYPE28 (NSTRAND)
Block Format Keyword Describes the multi-strand property set.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /PROP/TYPE28/prop_ID/unit_ID or /PROP/NSTRAND/prop_ID/unit_ID | |||||||||
| prop_title | |||||||||
| Mass | K | C | |||||||
| fct_ID1 | fct_ID2 | Y_SCAL | X_SCAL | ||||||
Definitions
| Field | Contents | SI Unit Example |
|---|---|---|
| prop_ID | Property
identifier (Integer, maximum 10 digits) |
|
| unit_ID | Unit Identifier (Integer, maximum 10 digits) |
|
| prop_title | Property
title (Character, maximum 100 characters) |
|
| Mass | Mass per unit
length (Real) |
|
| K | Stiffness for a length of
a unitary length (Real) |
|
| C | Damping coefficient of a
unitary length (Real) |
|
| fct_ID1 | Function identifier
defining
(Integer) |
|
| fct_ID2 | Function identifier
defining
(Integer) |
|
| Compression failure
strain Default = -1030 (Real) |
||
| Tension failure
strain Default = 1030 (Real) |
||
| Y_SCAL | Coefficient for the force
(homogeneous to a force) Default = 1.0 (Real) |
|
| X_SCAL | Coefficient for the strain
rate (homogeneous to a force) Default = 1.0 (Real) |
|
| Pulley general friction
coefficient (Real) |
||
| Strand general friction
coefficient (Real) |
||
| Type | Keyword "PULLEY" or
"STRAND" (left justified) (Character) |
|
| k | Pulley or strand number
(internal node number in the element) (Integer) |
|
| Friction coefficient at
pulley or along strand (Real) |
Comments
- To define the connectivity of multi-strand elements, refer to /XELEM.
- The force in the spring
is computed as:Linear spring:
(1) Nonlinear spring:(2) if or
Where, is the engineering strain:(3) and is the reference length of element.
- If
,
(4) - If
,
(5) - Pulley type friction is
defined (except at end nodes of the element).
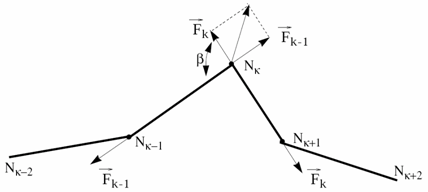
Figure 1.(6) - is the force in strand connecting nodes Nk-1 and Nk.
- Fk is the force in strand connecting nodes Nk and Nk+1.
- You can also define friction along strands.
- Specific friction coefficients is defined (different from general values) for some pulleys or for some strands (Line 6).
- If n is the total number of nodes of an element, strands are numbered from one to (n) and all pulleys (internal nodes) are numbered from 2 to (n-1).