/PROP/TYPE12 (SPR_PUL)

Format

Definitions

Example

/UNIT/2
unit for prop
                  Mg                  mm                   s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/PROP/SPR_PUL/1/2
pulley spring example with friction
#               Mass                               sensor_ID    Isflag     Ileng                Fric
              2.7e-5                                       0         0         0                   1
#                  K                   C                   A                   B                   D
               10000                .001                   0                   0                   0
#funct_ID1         H funct_ID2 funct_ID3 funct_ID4                     delta_min           delta_max
         1         0         0         0         0                             0                   0
#            Fscale1                   E             Ascalex                  H4
                   0                   0                   0                   0
# Fct_IDfr       Ifr            Yscale_F            Xscale_F               F_MIN               F_MAX
         2         1                   0                   0                -800                4500
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/1
non-linear elastic
#              Disp.               Force
#                  X                   Y
                  -1                -0.1                                                            
                   0                   0
                   1               10000				   
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/2
friction function 
#              Force                Fric
#                  X                   Y
               -1000                 0.2                                                            
                1000                 0.2
                2000                 0.3                                                            
                4000                 0.9
                5000                 1.0
               10000                 1.0				
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA

Comments

1. This property is modeled using a 3 node /SPRING element where node 1 and node 3 are the ends of the rope and node 2 is the pully location.

   
   
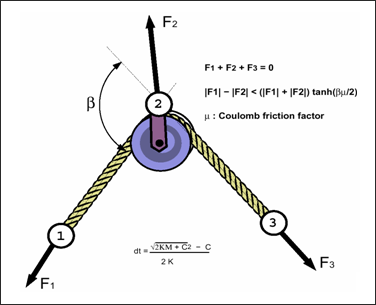
   Figure 1.

   Once node 1 slides to node 2 locking occurs as if there is a knot at node 1 that cannot move through the pully.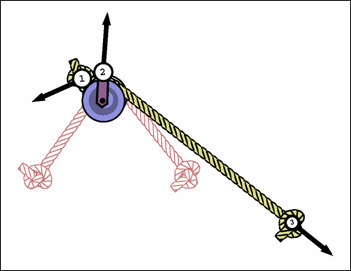

   
   
   Figure 2.

2. Force computation:
   • In case of I_leng =0 (flag I_leng is defined in Line 3), the force in the spring is computed as:(1)
     $$F=\mathrm{f}\left(\frac{{\delta }^1}{Ascal{e}_1}\right)\left[A_1+B_1\ln \left(\max \left(1,\left|\frac{{\dot{\delta }}^1}{D_1}\right|\right)\right)+E_1\mathrm{g}\left(\frac{{\dot{\delta }}^1}{F_1}\right)\right]+C_1{\dot{\delta }}^1+Hscal{e}_1\mathrm{h}\left(\frac{{\dot{\delta }}^1}{F_1}\right)$$

     With $-l_0<{\delta }^1<+\infty$

     Where, $\delta =l-l_0$ is the difference between the current length and the initial length of the spring element.

   • If I_leng=1, all input are per unit length.

     Spring mass = $M\cdot l_0$

     Spring stiffness = $\frac{K}{l_0}$

     Spring damping = $\frac{C}{l_0}$

     Spring inertia = $I\cdot l_0$

     Where, $l_0$ is the spring reference length.

   • The value of force in the spring is computed as:(2)
     $$F=\mathrm{f}\left(\frac{\epsilon }{Ascal{e}_1}\right)\left[A_1+B_1\ln \left(\max \left(1,\left|\frac{\dot{\epsilon }}{D_1}\right|\right)\right)+E_1\mathrm{g}\left(\frac{\dot{\epsilon }}{F_1}\right)\right]+C_1\dot{\epsilon }+Hscal{e}_1\mathrm{h}\left(\frac{\dot{\epsilon }}{F_1}\right)$$
     Where, $\text{ε}$ is the engineering strain:(3)

     $$\epsilon =\frac{\delta }{l_0}$$

     Force functions are given versus engineering strain and engineering strain rate.

     Failure criteria are defined with respect to strain. Input of negative/positive failure limit should be related to initial length $l_0$

3. If ${\delta }_{\min }^1$ (resp ${\delta }_{\max }^1$ ) is 0, no failure in the direction. The ${\delta }_{\min }^1$ must be negative. For linear springs, $\mathrm{f}\left(\delta \right)$ and $\mathrm{g}\left(\dot{\delta }\right)$ are null functions and A₁, B₁ and E₁ are not taken into account.
4. Spring is activated and/or deactivated by sensor:
   • If sens_ID ≠ 0 and I_sflag = 0, the spring element is activated by the sens_ID.
   • If sens_ID ≠ 0 and I_sflag = 1, the spring element is deactivated by the sens_ID.
   • If sens_ID $\ne$ 0 and I_sflag = 2, then:
     • The spring is activated and/or, deactivated by sens_ID. (if sensor is ON, spring is ON; if sensor is OFF, spring is OFF).
     • The spring reference length ( $l_0$ ) is the distance between spring node N1 and N2 at the time of the sensor's activation.
5. If a sensor is used for activating or deactivating a spring, the reference length of the spring at sensor activation (or deactivation) is equal to the nodal distance at time =0; except if sensor flag is equal to 2.
6. Friction models definition:

   
   
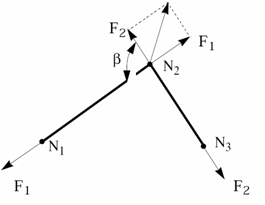
   Figure 3.

   • If fct_ID_fr and Fric = 0 (no friction), then $\left|F_1\right|=\left|F_2\right|$ .
   • If fct_ID_fr = 0 and Fric > 0, then constant Coulomb friction coefficient used: $\mu =Fric=\mathrm{const}.$
   • If fct_ID_fr > 0, then variable friction is calculated as a function on relative force between two pulley branches:

     I_fr = 0 (symmetrical behavior), $\text{Δ}F=\left|F_1-F_2\right|$

     I_fr = 1 (non-symmetrical behavior), $\text{Δ}F=F_1-F_2$

     Friction force $F_{fr}$ is computed as:(4)

     $$F_{fr}=\min \left\{\left|\text{Δ}F\right|,\max \left[0,\left(F_1+F_2\right)\cdot \tanh \left(\frac{\beta \cdot \mu }{2}\right)\right]\right\}\cdot sig\left(\text{Δ}F\right)$$
     Where,(5)

     $$\mu ={\text{f}}_{fr}\left(\frac{\text{Δ}F}{Xscale\_F}\right)\cdot Yscale\_F$$

     $\beta$

     Angle (radians unit)

     $f_{fr}$

     Function of fct_ID_fr

   • If I_fr = 1 (non-symmetrical behavior) and when F_min (or F_max) is reached, friction is switching permanently from the function definition to the constant value Fric.

     
     
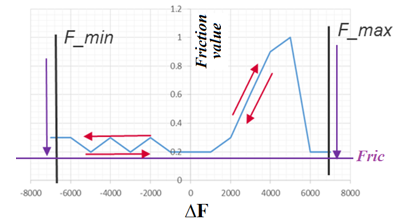
     Figure 4.

     Otherwise, the friction value is defined according to the input function fct_ID_fr.