/PROP/TYPE45 (KJOINT2)

Format

Definitions

Joint Types List

Example (Rotational)

#RADIOSS STARTER
/UNIT/2
unit for prop
                  kg                  mm                  ms
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/PROP/TYPE45/2/2
Revolute 
### - Define angle limit < 0.52rad 
### - And define friction moment 100GPa to block angle (if it reached the limit)
#     Type                  KN                 SCF                  CR  SENSORID
         2                   0                   0                   0         0
#                KR1Func_ID_Kr                SA1-                SA1+  Icomb_r1
                   0         0                   0                 .52         0
#                CR1Func_ID_Cr
                   0         0
#               KFR1                 FM1   FCT_FM1
                   0                 100         0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA

Example (Translational)

#RADIOSS STARTER
/UNIT/2
unit for prop
                  kg                  mm                  ms
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/PROP/TYPE45/12/2
Translational 
### - define displacement limit: -100mm ~ 100 mm
#     Type                  KN                 SCF                  CR  SENSORID
         6                   0                   0                  .2         0
#                KX1Func_ID_Kx                SD1-                SD1+  Icomb_t1
                   0         0                -100                 100         0
#                CX1Func_ID_Cx
                   0         0
#               KFX1                 FF1   FCT_FF1
                1000                   0         0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA

Comments

1. Spring element:
   • The identifier must be unique in each element family, but it is advised to have a unique element identifier in the global model for each element type.
   • More than one spring block can be used to define a part.
2. Spring DOF:
   • Joint properties are defined in a local coordinate system of the joint element.
   • The total number of joint DOF computed in the local coordinate system frame is six:

     ${\delta }_{{\mathbf{X}}^{\prime }},{\delta }_{{\mathbf{Y}}^{\prime }},{\delta }_{{\mathbf{Z}}^{\prime }},{\theta }_{{\mathbf{X}}^{\prime }},{\theta }_{{\mathbf{Y}}^{\prime }},{\theta }_{{\mathbf{Z}}^{\prime }}$

   • Blocked and free DOF are distinguished for each joint type.
   • The blocked DOF are characterized by a constant stiffness. By default, if no stiffness value is entered, the value of the stiffness is automatically computed to preserve the time step.
   • The translational and rotational DOF are defined as:(1)
     $$\delta =d{x}_2-d{x}_1$$
     Where, $d{x}_1$ and $d{x}_2$ are total displacements of two joint nodes in the local coordinate system.(2)

     $$\theta ={\theta }_2-{\theta }_1$$

     Where, ${\theta }_1$ and ${\theta }_2$ are total relative rotations of two connected body axes, with respect to the local coordinate system of the joint.

   • If sens_ID is defined, then the joint becomes fully blocked (all degrees of freedom) when the sensor is activated.
3. Forces and moments calculation:
   • The force in direction $\mathbf{\delta }$ is computed as:
     Linear spring:(3)

     $$\mathbf{F}={\mathbf{K}}_{ti}\mathbf{\delta }+{\mathbf{C}}_{ti}\dot{\mathbf{\delta }}$$

     $K_{ti}$ : translational stiffness $\left(K_{tx},K_{ty},K_{tz}\right)$

     $C_{ti}$ : translational viscosity $\left(C_{tx},C_{ty},C_{tz}\right)$

     Nonlinear spring:(4)

     $$F=K_{ti}\mathrm{f}\left(\delta \right)+C_{ti}\mathrm{g}\left(\dot{\delta }\right)$$
   • The moment in $\mathbf{\theta }$ direction is computed as:
     Linear spring:(5)

     $$\mathbf{M}={\mathbf{K}}_{\mathit{ri}}\mathbf{\theta }+{\mathbf{C}}_{\mathit{ri}}\dot{\mathbf{\theta }}$$

     $K_{ri}$ : rotational stiffness ( $\left(K_{rx},K_{ry},K_{rz}\right)$ )

     $C_{ri}$ : rotational viscosity ( $\left(C_{rx},C_{ry},C_{rz}\right)$ )

     Nonlinear spring:(6)

     $$\mathbf{M}={\mathbf{K}}_{\mathit{ri}}\mathrm{f}\left(\mathbf{\theta }\right)+{\mathbf{C}}_{\mathit{ri}}\mathrm{g}\left(\dot{\mathbf{\theta }}\right)$$
   • The joint length may be, but is not necessarily equal to 0. It is recommended to use a 0 length spring to define a spherical joint or a universal joint.
   • To satisfy the global balance of moments in a general case, correction terms in the rotational DOF are calculated as:(7)
     $${\mathbf{M}}_{\theta x}={\mathbf{M}}_{\theta x}+{\mathbf{L}}_y\times {\mathbf{F}}_z-{\mathbf{L}}_z\times {\mathbf{F}}_y$$
     (8)
     $${\mathbf{M}}_{\theta y}={\mathbf{M}}_{\theta y}+{\mathbf{L}}_z\times {\mathbf{F}}_x-{\mathbf{L}}_x\times {\mathbf{F}}_z$$
     (9)
     $${\mathbf{M}}_{\theta z}={\mathbf{M}}_{\theta z}+{\mathbf{L}}_x\times {\mathbf{F}}_y-{\mathbf{L}}_y\times {\mathbf{F}}_x$$

     Joints do not have user-defined mass or inertia, so the nodal time step is always used.

4. Stiffness of spring
   • Coefficients $K_{ti}$ and $K_{ri}$ are used as constant stiffness, if there are no user-defined functions. If a function is defined, the corresponding stiffness coefficient becomes a scale factor for the function.
   • If K_n = 0, the blocking stiffness area is automatically computed at the beginning of the computation for both translational and rotational blocked DOF, in order to preserve the time step. These values are also selected according to the physics and must be higher than the stiffness of the neighboring elements.
   • If K_n = 0, then Scf is a scaling factor applied to both translational and rotational blocking stiffness. If K_n > 0, then Scf is applied only on blocking rotational stiffness. This parameter can be used to manually adjust the blocking stiffness in rotation.
5. Viscous of spring
   • Coefficients $C_{ti}$ and $C_{ri}$ are used as linear viscosity coefficients, if there are no user-defined functions. If a function is defined, the corresponding coefficient becomes a scale factor for the function.
   • There are two ways to introduce viscous damping:
     • Defining a critical damping (for blocked DOF only):

       Viscous damping is defined in terms of the critical damping factor. The critical damping coefficient is calculated using the blocking stiffness value of the element. The mass and inertia are equal to half of the values for each rigid body connected to the joint. The approximation is then satisfactory, if only one joint is connected to each rigid body. Otherwise, the critical damping is over-estimated; in which case, the damping factor in the Radioss input should be decreased. The same damping is applied to all blocked DOF.

     • User-defined constant or nonlinear damping:

       It is possible to define independent damping parameters for each free DOF.

6. Friction
   • Friction is not activated, if K_fti or K_fri are not defined.
   • FF_i and FM_i are used as constant friction force and moment, if there are no user defined functions. If the friction function number is not 0, FM_i and FF_i become a scale factor for the functions (default = 1.0).
7. Spring limit
   • If a non-zero value is specified for SD_i- or SD_i+, then an additional penalty force is applied to prevent the displacement to exceed SD_i+ for positive displacement and SD_i- for negative displacement. This penalty force is computed using K_fti.
   • If a non-zero value is specified for SA_i- or SA_i+, then an additional penalty moment is applied to prevent the angle to exceed SA_i+ for positive rotation or SA_i- for negative rotation. This penalty moment is computed using K_fri
8. Skew of spring
   • If Skew_ID₁ is defined, the initial local coordinate system is defined by Skew_ID₁. If Skew_ID₁ = 0, the local coordinate system is computed according to the additional nodes of the spring. Refer to /SPRING for more information.
   • If Skew_ID₂ is defined, rotation angles of the joint are initialized according the rotation between Skew_ID₁ and Skew_ID₂. Values of the initial angles can be check in the Starter output file. For revolute (TYPE2), cylindrical (TYPE3) and planar (TYPE4) joints only ${\theta }_X$ can be initialized. The first axis of Skew_ID₁ and Skew_ID₂ must be parallel.

     
     
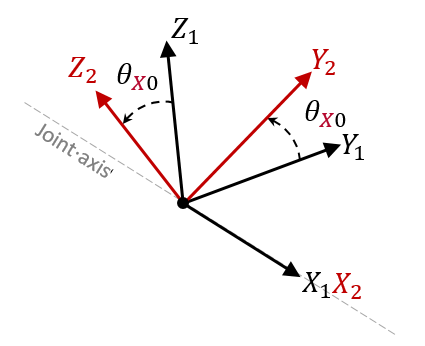
     Figure 1. Computation of Initial Rotation Angle for Revolute Joint (TYPE2)

   • If Skew_ID₂ is non-zero and Skew_ID₁ =0, then Skew_ID₁ is the global coordinate system.
   • The local coordinate system orientation is updated according node_ID₁ (/SPRING) rotation.
9. Combined stop displacements/angles:
   • If Icomb_t_i = 0: the stop displacements are independent (default) as shown in Figure 2. Stop displacement will be checked separately in each direction.
   • If Icomb_t_i = 1: the stop displacements of all the free translational DOF are combined. The stopping criteria is no longer applied on the displacement but on the norm of the combined displacements see Figure 3.
   • 2 or 3 stop displacements can be combined
   • If stop displacements are combined, the same value of SDi- and SDi+ must be used for each DOF.
   • The above descriptions for stop displacements also apply for stop angles defined using Icomb_r_i.

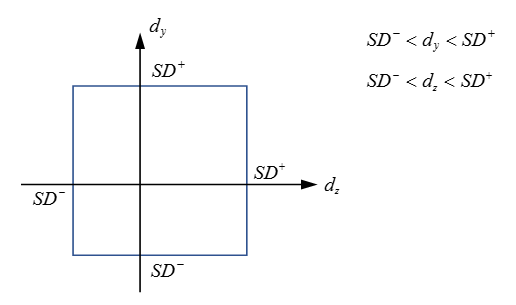
Figure 2. Planar Joint with Independent Stop Displacements, Icomb_t_i=0

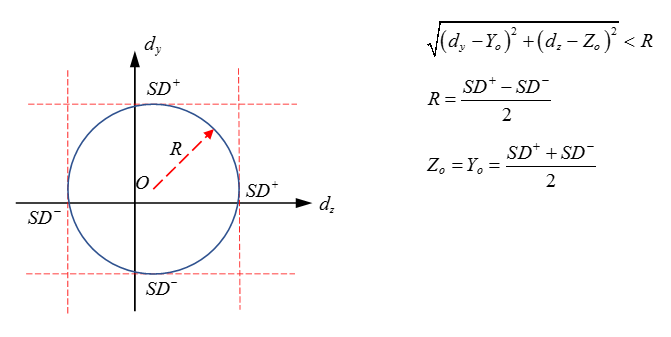
Figure 3. Planar Joint with 2 Combined Stopping Displacements, Icomb_t_i=1