/MAT/LAW69
ブロックフォーマットキーワード この材料則は/MAT/LAW42 (OGDEN)の拡張で、Ogden、Mooney-Rivlin材料モデルを使用して指定された超弾性および非圧縮性材料を定義します。
通常は、非圧縮性のゴム、ポリマー、フォーム、およびエラストマーのモデル化に使用されます。材料パラメータは、単軸引張および圧縮試験の工学応力ひずみ曲線から計算されます。シェルおよびソリッド要素で使用されます。
フォーマット
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /MAT/LAW69/mat_ID/unit_ID | |||||||||
| mat_title | |||||||||
| law_ID | fct_IDblk | v | Fscaleblk | N_pair | Icheck | ||||
| fct_ID1 | |||||||||
定義
| フィールド | 内容 | SI 単位の例 |
|---|---|---|
| mat_ID | 材料識別子 (整数、最大10桁) |
|
| unit_ID | 単位識別子。 (整数、最大10桁) |
|
| mat_title | 材料のタイトル (文字、最大100文字) |
|
| 初期密度 (実数) |
||
| law_ID | 超弾性材料モデルタイプ 2 (整数)
|
|
| fct_IDblk | 体積係数を相対体積の関数としてスケーリングする関数 6 (整数) |
|
| v | ポアソン比。 デフォルト = 0.495(実数) |
|
| Fscaleblk | fct_IDblkのスケールファクター。 デフォルト = 1.0(実数) |
|
| N_pair | ひずみエネルギー密度関数(W)の表現にある材料パラメータのペア(
pとαp)材料パラメータは、指定された応力ひずみ曲線(fct_ID1)から計算されます。 (N_pair ≤ 5) デフォルト = 2(整数) |
|
| Icheck | 材料パラメータ(
pとαp)の妥当性チェック
(整数) パラメータフィッティングは圧縮および引張試験データを使用します:
パラメータフィッティングは引張試験データのみを使用します:
|
|
| fct_ID1 | 単軸引張および圧縮試験による工学応力ひずみ曲線の関数識別子。 (整数) |
例(Mooney-Rivlin 定式化)
#RADIOSS STARTER
/UNIT/1
unit for mat
Mg mm s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW69/1/1
LAW69 rubber
# RHO_I
1E-9
# LAW_ID FCT_ID NU FSCALE N_PAIR ICHECK
2 0 .495 0 2 0
# FCT_ID1
2
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 3. FUNCTIONS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/2
LAW69 e.strain e.stress
# X Y
0 0
.03 .30
.06 .55
.10 .80
.20 1.4
.30 2.0
.50 2.7
.70 3.4
1.0 4.0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|例(Ogden 定式化)
#RADIOSS STARTER
/UNIT/1
unit for mat
Mg mm s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW69/1/1
LAW69 rubber
# RHO_I
1E-9
# LAW_ID FCT_ID NU FSCALE N_PAIR ICHECK
1 0 .495 0 2 0
# FCT_ID1
2
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 3. FUNCTIONS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/2
LAW69 e.strain e.stress
# X Y
0 0
.03 .30
.06 .55
.10 .80
.20 1.4
.30 2.0
.50 2.7
.70 3.4
1.0 4.0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|コメント
- 現在のところ、Radiossで使用できるテストデータは、次の変形理論に基づくデータです。
単軸引張および圧縮。
入力応力ひずみデータ(fct_ID1)は、工学ひずみの関数としての工学応力です。工学ひずみは、負の値(圧縮)から正の値(引張)の範囲で単調に増加する必要があります。圧縮では、工学ひずみを-1.0より大きくする必要があります。fct_ID1のデータが不完全であると(引張データのみ)、引張のみが考慮されます。
- 使用されるひずみエネルギー密度定式化は、law_IDに基づきます。
- law_ID = 1 (Orgden則):
(1) - law_ID = 2 (Mooney-Rivlin則):
(2)
- law_ID = 1 (Orgden則):
- Radiossは、応力ひずみ曲線(fct_ID1)を読み出してから、非線形最小2乗フィッティングを使用して、対応するパラメータペアを計算します。
- 古典的なOgden則では、パラメータペアは pおよびαp (p=1,...5, max of N_pair = 5)
- Mooney-Rivlin則では、パラメータペアは pおよびαp (p=1,2, N_pair = 常に2)
- 非線型最小2乗フィッティングの精度を向上させるために、以下を推奨します。
- 実験データ曲線は、横軸点が一様に分布するスムーズな単調増加関数を表します。実験データ曲線内のデータ点の数は、パラメータペアN_pair)の数より多くする必要があります。
- N_pair ≥ 3の場合は、テストデータのカバー率を引張ひずみで100%以上、圧縮ひずみで50%以上にする必要があります。
- N_pair は、フィッティング手順での減衰を回避するために大きい値に設定しないようにする必要があります。
- Radiossは、入力(実験)と、フィッティングプロセス中に決定された対応する材料パラメータを使用してひずみエネルギー密度関数(W))から計算された応力ひずみ曲線間の“フィッティングの平均誤差”を出力します。最大“フィッティングの平均誤差”は10%を超えないようにする必要があります。
- この材料則は、
(p=1,…5)があらゆる荷重条件のパラメータペアに最適な場合に安定します。デフォルトで、RADIOSSは、このような条件(Icheck= 2)を考慮して曲線をあてはめようとします。
あてはまる曲線が見つからなかった場合は、弱い方の条件(Icheck= 1: )が使用されます。後者は、初期せん断超弾性係数( )が正となるようにするために必要な条件です。
- 材料
の非圧縮性は、密度の変化に比例して圧力を計算するペナルティアプローチを使用して求められます:
(3) ここで、fはfct_IDblkblkの関数です。
比例係数(K)は、一般的には非常に高い値になる体積係数です。これにより、非圧縮性条件(J=1)に違反した場合、圧縮抵抗が非常に高い値となります。ヤコビアン(J)は、初期要素体積に対する現在の要素体積の比率として解釈することができます。
fct_IDblkは、非圧縮性をさらに制御します(図 1参照)。これにより、Jの値に基づく体積係数値の増加が可能になります。デフォルトで、関数識別子は0で、体積スケーリング関数の値は1に等しくなります。密度のばらつきが小さくなるように、つまり、Jの値が1に近付くように、LAW69コンポーネントの密度分布を出力および制御することをお勧めします。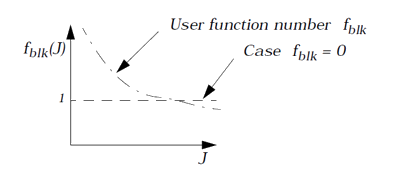
図 1. - ポアソン比vは、体積弾性率(K)の計算のみに使用されます。
純粋な非圧縮性材料の場合は、 です。このポアソン比の値は、体積弾性率(K)の無限大値を意味します。そのため、非圧縮性材料に推奨されるポアソン比は (デフォルト)。陰解法および陽解法シミュレーションの場合は、ポアソン比を高くすると、時間ステップ値の減少や発散につながる可能性があります。
- 粘性効果を含めるには、この材料則と共に/VISC/PRONYを使用する必要があります。
- この材料則の詳細については、“Non-Linear Elastic Deformations”(R.W Ogden、Ellis Horwood著、1984年)をご参照ください。