/INTER/TYPE6

Block Format Keyword This interface is used to simulate contact between two rigid bodies with tabulated input of the contact force. It works similar to interface TYPE3. Contact force between the bodies can be input as a function of maximal penetration. The interface also allows you to input a force function for unloading.

Description

The following conditions should be fulfilled for this interface:

The segments of two contact surface must face each other (example: the surface normals must be oriented from one surface to the other)
The interface only works with segments connected to solid or shell elements; two contact surface must not share the same node (must be part of 2 different rigid bodies)
User-defined interface stiffness can reduce the time step

Format

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(9)
/INTER/TYPE6/`inter_ID`/`unit_ID`
`inter_title`
`surf_ID`₁	`surf_ID`₂
`Sfric`		`Fric`		`Gap`		`T`_start	`T`_stop
	`I`_RS	`I`_Rm	`Inacti`	`fct_ID`_ff	`fct_ID`_fv	`Ascale`_f	`Ascale`_v
`fct_ID`_Id	`I`_form	`Ascale`_x		`Fscale`_Id		`Icor`
`fct_ID`_ul		`Stiff`		`Fscale`_ul
`Visc`		`fct_ID`_dv	`fct_ID`_df	`Fscale`_v

Definitions

Field	Contents	SI Unit Example
`inter_ID`	Interface identifier (Integer, maximum 10 digits)
`unit_ID`	Unit identifier (Integer, maximum 10 digits)
`inter_title`	Interface title (Character, maximum 100 characters)
`surf_ID`₁	Rigid surface 1 identifier. (Integer)
`surf_ID`₂	Rigid surface 2 identifier. (Integer)
`Sfric`	Static friction force. (Real)	$[N]$
`Fric`	Coulomb friction. (Real)
`Gap`	Gap for impact activation. (Real)	$[m]$
`T`_start	Interface activation time. Default = 0.0 (Real)	$[s]$
`T`_stop	Interface deactivation time. Default = 1.0e30 (Real)	$[s]$
`I`_RS	Renumbering flag for segments of the first surface. = 0 If segment is connected to a solid element, its normal is reversed if entering the solid element (the segment is renumbered). = 1 Normal is always reversed (segment 1234 is read 2143). = 2 Normal is never reversed (segments connected to a solid element are not renumbered). (Integer)
`I`_Rm	Renumbering flag for segments of the second surface (same as `I`_RS). = 0 If segment is connected to a solid element, its normal is reversed if entering the solid element (the segment is renumbered). = 1 Normal is always reversed (segment 1234 is read 2143). = 2 Normal is never reversed (segments connected to a solid element are not renumbered). (Integer)
`Inacti`	Deactivation flag of stiffness in case of initial penetrations. = 0 No action. = 5 Gap is variable with time and initial gap is adjusted as: ${gap}_{0} = Gap - P_{0}$ Where, $P_{0}$ is the initial penetration. 7 (Integer)
`fct_ID`_ff	Friction multiplier function vs. normal force. (Integer)
`fct_ID`_fv	Friction multiplier function vs. sliding velocity. (Integer)
`Ascale`_f	Abscissa scale factor for velocity functions (`fct_ID`_ff and `fct_ID`_dv). (Real)	$[\frac{m}{s}]$
`Ascale`_v	Abscissa scale factor for force functions (`fct_ID`_ff and `fct_ID`_dv). (Real)	$[N]$
`fct_ID`_Id	Force vs penetration curve function identifier. This function should be positive in both force and displacement. (Integer)
`I`_form	Contact formulation flag. 1 = 0 Nonlinear elastic. = 1 Nonlinear elasto-plastic with an unloading curve which must be defined. = 2 Nonlinear elasto-plstic with decoupled hardening. (Integer)
`Ascale`_x	Abscissa scale factor on `fct_ID`_Id and `fct_ID`_ul. Default = 1.0 (Real)	$[m]$
`Fscale`_Id	Ordinate scale factor on `fct_ID`_Id. Default = 1.0 (Real)	$[N]$
`Icor`	Adjusting force flag, due to initial intersection. 2 = 0 Off = 1 On (Integer)
`fct_ID`_ul	Force vs penetration curve for unload function identifier. This function should be positive in both force and displacement and always less than the loading curve. Not used if `I`_form = 2. (Integer)
`Stiff`	Loading/unloading stiffness used when transitioning between curves. Required input if `I`_form = 1, 2.	$[\frac{N}{m}]$
`Fscale`_ul	Ordinate scale factor for unload `fct_ID`_ul. Default = 1.0 (Real)	$[N]$
`Visc`	Damping coefficient. (Real)	$[\frac{Ns}{m}]$
`fct_ID`_dv	Damping force function vs. penetration velocity. (Integer)
`fct_ID`_df	Damping multiplier function vs. normal force. (Integer)
`Fscale`_v	Ordinate scale factor on `fct_ID`_dv. (Real)	$[N]$

Comments

The loading curve fct_ID_Id should always be given.
For I_form =0, the unloading curve is not considered and loading and unloading use the same curve fct_ID_Id.
For I_form =1, the unloading curve fct_ID_ul is considered and:
- When the unloading curve fct_ID_ul is not defined, then loading follows the fct_ID_Id and unloading follows a straight curve with slope Stiff down to zero and remain equal to zero. Reloading Radioss jumps from zero to the loading function fct_ID_Id along a straight curve with slope Stiff.
- When both the loading and unloading curves are defined (the unloading curve should be lower than the loading curve) then during unloading Radioss jumps from loading to unloading curve following a straight curve with slope Stiff. Reloading Radioss jumps from fct_ID_ul unloading curve to loading curve fct_ID_Id along a straight curve with slope Stiff.
Some of the cases are shown below: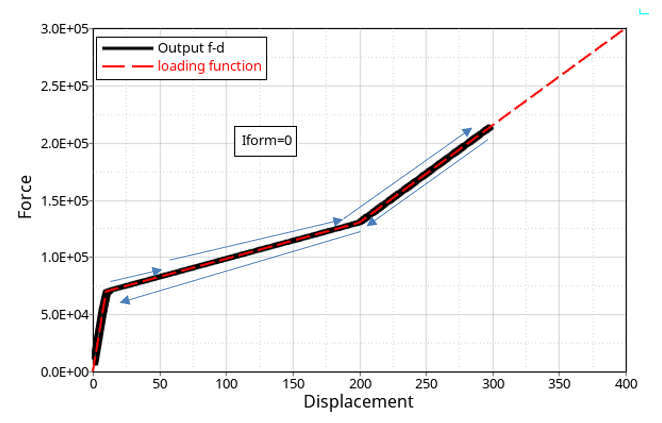

Figure 1. I_form = 0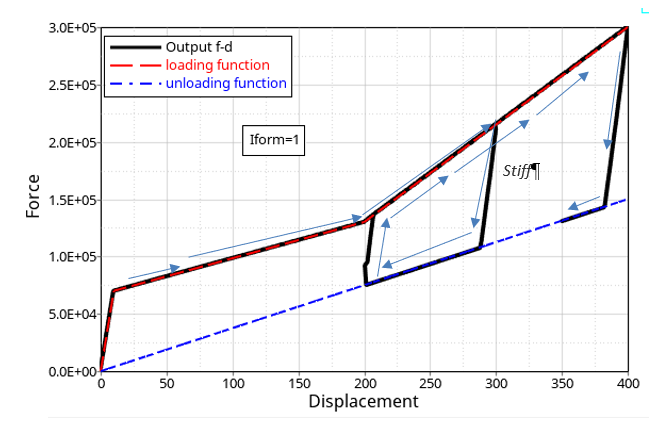

Figure 2. I_form = 1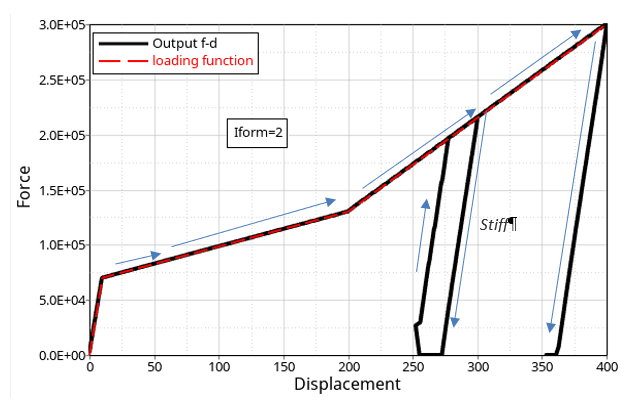

Figure 3. I_form = 2
If I_form =1 and Icor =1, the interface force at t=0 is set to a value from the unloading function fct_ID_ul, which corresponds to the initial penetration. If the unloading function is not defined, the initial force is set to zero.
Tangent friction force, F_t is calculated as:(1)
$F_{t} = Sfric + μ (F_{n}, F_{t}) \cdot F_{t}$

Where,

$F_{n}$

The normal force

$μ$ ( $F_{n}$ , $F_{t}$ )

Dynamic friction coefficient defined as:

(2)
$μ (F_{n}, F_{t}) = Fric \cdot f_{ff} (F_{n}) \cdot f_{fv} (v_{t})$

Where,

$v_{t}$

Sliding velocity

$f_{f f}$ and $f_{f v}$

Functions of fct_ID_ff and fct_ID_fv
Damping force, F_damp is calculated as:(3)
$F_{damp} = f_{df} (F_{n}) \cdot (Visc + f_{dv} (v_{n}))$

Where,

$v_{n}$

Penetration velocity

$f_{d f}$ and $f_{d v}$

Functions of fct_ID_df and fct_ID_dv