/INTER/TYPE11
ブロックフォーマットキーワード このインターフェースは、エッジ間またはライン間の衝撃をシミュレートします。ラインは、ビームやトラス要素、またはシェルのエッジやスプリング要素です。
- 衝撃はメインラインとセカンダリラインの間で発生します。
- セカンダリラインは、1つまたは複数のメインラインに衝撃を与えることができます。
- 1つのラインは、メイン側およびセカンダリ側に属することができます。これにより自己接触が可能になります。
- このインターフェースをインターフェース/INTER/TYPE7に追加して使用すると、インターフェースTYPE7のエッジ対エッジの制限を解消することができます。
フォーマット
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /INTER/TYPE11/inter_ID/unit_ID | |||||||||
| inter_title | |||||||||
| line_IDs | line_IDm | Istf | Ithe | Igap | Irem_gap | Idel | |||
| Stmin | Stmax | %mesh_size | dtmin | Iform | sens_ID | ||||
| Stfac | Fric | Gapmin | Tstart | Tstop | |||||
| IBC | Inacti | VISs | VISF | Bumult | |||||
| fric_ID | |||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| Kthe | fct_IDK | AscaleK | Tint | Ithe_form | |||||
| Frad | Drad | ||||||||
定義
| フィールド | 内容 | SI 単位の例 |
|---|---|---|
| inter_ID | インターフェースの識別子 (整数、最大10桁) |
|
| unit_ID | 単位識別子. (整数、最大10桁) |
|
| inter_title | インターフェースのタイトル (文字、最大100文字) |
|
| line_IDs | セカンダリラインの識別子。 3 (整数) |
|
| line_IDm | メインライン識別子。 3
(整数) |
|
| Istf | 剛性定義フラグ。
(整数) |
|
| Ithe | 熱伝導フラグ
(整数) |
|
| Igap | ギャップ/要素オプションフラグ
(整数) |
|
| Irem_gap | 自己接触において要素サイズがギャップ値より小さい場合に隣接セカンダリラインを非アクティブ化するためのフラグ。 18
|
|
| Stmin | 最小剛性(Istf ≠ 1の場合にのみ使用) (実数) |
|
| Stmax | 最大剛性(Istf ≠ 1の場合にのみ使用) デフォルト = 1030(実数) |
|
| %mesh_size | メッシュサイズのパーセンテージ(Igap = 3の場合にのみ使用) デフォルト = 0.4(実数) |
|
| dtmin | 最小インターフェース時間ステップ 12 (実数) |
|
| Iform | 摩擦ペナルティ定式化のタイプ。 14
(整数) |
|
| sens_ID | インターフェースをアクティブ化 / 非アクティブ化するためのセンサーID 13 IDセンサーが定義されている場合は、インターフェースのアクティブ化 / 非アクティブ化はセンサーに基づき、Tstart、Tstopには基づきません。 (整数) |
|
| Idel | 節点およびセグメントの削除フラグ。 4
(整数) |
|
| Stfac | インターフェースのメイン側に適用される剛性スケールファクター(Istf ≠ 1の場合) デフォルト = 1.0(実数) |
|
| インターフェース剛性(Istf = 1の場合) デフォルト = 1.0(実数) |
||
| Fric | Coulomb摩擦。 (実数) |
|
| Gapmin | 衝撃アクティブ化の最小ギャップ (実数) |
|
| Tstart | 開始時間。 (実数) |
|
| Tstop | 一時的な非アクティブ化の時間 (実数) |
|
| IBC | 接触時の境界条件の非アクティブ化フラグ (ブーリアン) |
|
| Inacti | 非アクティブ化剛性フラグ 11
(整数) |
|
| VISs | インターフェース剛性の臨界減衰係数 デフォルト = 0.05(実数) |
|
| VISF | 接触面摩擦の臨界減衰係数 デフォルト = 1.0(実数) |
|
| Bumult | ソート係数。 12 13 デフォルト = 0.20(実数) |
|
| fric_ID | 選択されたパートのペアについての摩擦定義の摩擦識別子
(整数) |
|
| Kthe | 熱交換係数(fct_IDK = 0の場合) 15 デフォルト = 0.0(実数) |
|
| 熱交換スケールファクター(fct_IDK ≠ 0の場合) 15 デフォルト = 1.0(実数) |
||
| fct_IDK | 接触圧力に対する熱交換定義の識別子 デフォルト = 0(整数) |
|
| AscaleK | fct_IDKの横軸のスケールファクター デフォルト = 1.0(実数) |
|
| Tint | インターフェース温度 15 (実数) |
|
| Ithe_form | 熱接触定式化フラグ
(整数) |
|
| Frad | 放射係数 15 (実数) |
|
| Drad | 放射計算の最大距離 15 (実数) |
境界条件の非アクティブ化フラグ: IBC
| (1)-1 | (1)-2 | (1)-3 | (1)-4 | (1)-5 | (1)-6 | (1)-7 | (1)-8 |
|---|---|---|---|---|---|---|---|
| IBCX | IBCY | IBCZ |
定義
| フィールド | 内容 | SI 単位の例 |
|---|---|---|
| IBCX | 衝撃時のX境界条件の非アクティブ化フラグ
(ブーリアン) |
|
| IBCY | 衝撃時のY境界条件の非アクティブ化フラグ
(ブーリアン) |
|
| IBCZ | 衝撃時のZ境界条件の非アクティブ化フラグ
(ブーリアン) |
コメント
- ラインがスプリング要素である場合は、ゼロ以外のGapmin値を入力する必要があります。
- SPMDの場合、line_IDmによって定義される各メインセグメントを1つの要素に関連付ける必要があります(ボイド要素の場合もあります)。
- セカンダリおよびメインラインはラインを用いて定義されます。自己衝撃接触は、line_IDs > 0およびline_IDm = 0の際に定義されます。
- フラグ Idel = 1のCPUコストはIdel = 2よりも高くなります。
- Gapminのデフォルト値は、次のように計算されます:
(1) このとき、- メインサーフェスのギャップ
- シェル要素に対するメイン要素の平均板厚
- ソリッド要素の最小辺の長さ。
- ビーム要素とトラス要素の最小断面。
- セカンダリサーフェスのギャップ: セカンダリ側要素に適用されることを除いて、 と同じ計算。
- 可変ギャップ
- Igap = 1000の場合、ギャップは一定で、Gapminと同じです。
- Igap = 1の場合、ギャップは可変で、衝撃ごとに以下のように計算されます:
(2) - Igap = 3の場合、ギャップは可変で、衝撃ごとに以下のように計算されます:
(3) ここで、- メイン要素のギャップ
- ここで、 : シェル要素に対するメイン要素の板厚
- はソリッド要素の最小辺の長さ
- はトラスおよびビーム要素の断面
- スプリング要素の場合
- セカンダリ側要素に適用されることを除いて、同様に計算されます
- 要素の短いエッジの長さ
- セカンダリ節点に結合された要素の短いエッジ長さ
可変ギャップは常にGapmin以上です。
- 接触剛性
剛性係数の値に制限はありません(ただし、値が1.0より大きいと、最初の時間ステップが短くなる場合があります)。シェル、ソリッドおよびビーム要素の接触剛性は次のように計算されます:
Istf =1の場合:(4) Istf = 2、3、4または5の場合:(5) ここで、-
は、Istf ≠ 1の場合、メインセグメントの剛性
とセカンダリセグメントの剛性
の両方から、次のように計算されます:
Istf = 2、
Istf = 3、
Istf = 4、
Istf = 5、
- ここで、
はメインセグメントの剛性で、次のように計算されます:メインセグメントがシェル上に存在するか、シェルとソリッドによって共有されている場合
(6) メインセグメントがソリッド上に存在する場合:(7) ここで、- セグメント面積
- ソリッドの体積
- 体積弾性率
-
は考慮される相当節点剛性:節点がシェル要素に結合されている場合:
(8) 節点がソリッド要素に結合されている場合:(9)
/PROP/VOIDと/MAT/VOIDを使用する際、ボイド材料の材料プロパティと板厚が入力されなければなりません。そうしないと、ボイド要素の接触合成はゼロになります。シェル要素の剛性が接触計算に使用されるため、これは、ボイドシェル要素がソリッド要素と要素を共有する場合に特に重要です。
他の要素に結合されていないスプリング要素には、Istf=1を使用し、Stfacを用いて接触剛性を指定します。それ以外の場合、接触は検出されません。
-
は、Istf ≠ 1の場合、メインセグメントの剛性
とセカンダリセグメントの剛性
の両方から、次のように計算されます:
- 境界条件の非アクティブ化は、サーフェス1の節点に適用されます。
- 節点がスプリング要素に属している場合にInacti = 3であると、初期エネルギーが発生することがあります。インターフェースに対する高周波数の影響を回避するためには、Inacti =5ではなく、Inacti = 6が推奨されます。
図 1. - ソートアルゴリズムを高速化するには、ソート係数Bumultを使用します。
- Bumultのデフォルト値は、150万個を超える節点を持つモデルでは0.30に、250万個を超える節点を持つモデルでは0.40に自動的に増やされます。
- この接触内の2次節点のタイムステップがdtmin未満になると、2次節点は接触から証拠され、警告のメッセージが出力ファイルに出力されます。このdtmin値は、/DT/INTER/DEL内に入力されるあらゆるモデルインターフェースの最小タイムステップより優先されます。
- インターフェースのアクティブ化 / 非アクティブ化のためにsens_IDが定義されている場合、TstartおよびTstopは考慮されません。
- fric_IDが定義されている場合、接触摩擦は/FRICTIONで定義され、この入力カード内の摩擦入力Fricは使用されません。
摩擦定式化の場合:
摩擦ペナルティ定式化Iform- Iform = 1(デフォルト)の粘性定式化の場合、摩擦力は次のとおりです:
(10) このとき、粘着力は以下のように計算されます:
ここで、
- Iform = 2の粘性定式化の場合、摩擦力は次のとおりです:
(11) このとき、粘着力は以下のように計算されます:
ここで、
は、メインセグメントに相対するセカンダリ節点の接線速度
陰解析と低速度衝撃陽解析には、Iform = 2が推奨されています。
- Iform = 1(デフォルト)の粘性定式化の場合、摩擦力は次のとおりです:
- 熱交換:Ithe=1(熱伝導をアクティブ化)にすることで、接触の熱交換と熱摩擦を考慮します。
- Ithe = 0の場合、熱交換はシェルと一定温度接触Tintの間で行われます。
- Ithe_form = 1の場合、熱交換はすべての接触片間で行われます。
TintはIthe_form=0の場合にのみ使用されます。この場合、メイン側の温度は一定(Tintに等しい)と想定されます。Ithe_form=1の場合、Tintは考慮されません。このため、メイン側の節点温度が考慮されます。
Ithe > 1の場合、セカンダリ側の材料は、熱伝導に有限要素定式化を使用する熱材料とする必要があります(/HEAT/MAT)。
熱交換係数:- fct_IDK = 0の場合、Ktheは熱交換係数で、熱交換は熱交換サーフェスのみに依存します。
- fct_IDK ≠ 0の場合、Ktheはスケールファクターで、熱交換は接触圧力に依存します:
(12) ここで、 はfct_IDKの関数です。
- 熱伝導は、セカンダリ節点がギャップ内に入った場合に計算されます。
- 放射が接触で考慮されるのは、
で、セカンダリ節点のメインセグメントまでの距離、dが次の場合です:
(13) ここで、 は放射計算の最大距離です。 のデフォルト値は、以下の最大値として計算されます:- 全節点中のGapの上限値(時間0における)
- セカンダリ要素の最小辺長
の値は、Radioss Engineのパフォーマンスの減少を引き起こすかもしれないため、高すぎる値に設定しないことを推奨します。熱交換は、メインからセカンダリの方向のみで計算されます。
熱伝導の放射は以下のように計算されます:(14) ここで、(15) ここで、- シュテファンボルツマン定数
- セカンダリサーフェスの輻射率
- メインサーフェスの輻射率
- 要素サイズが接触のギャップより小さく自己接触がある場合、近傍のセカンダリラインとの物理的な接触は起こり得ません。自己接触の場合、Irem_gap=2を使用すると、隣接するセカンダリラインセグメントの接触が削除されます。各メインラインについて、要素の結合性を用いて近傍のラインを決定します。続いて、少なくとも1つの節点の曲線距離が (初期設定で)より小さいセカンダリラインが、このメインラインと共に接触から消去されます。メインラインとセカンダリラインとの間の実際の距離も、近傍のすべてのラインが消去されたかを検証するためにチェックされます。
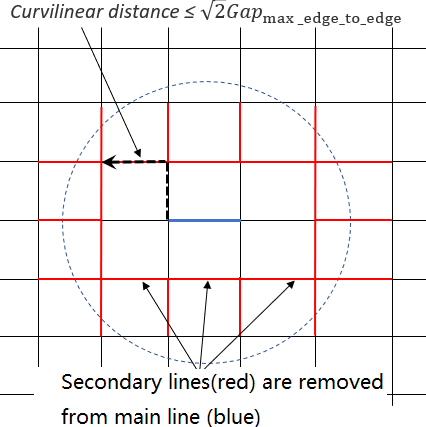
図 2. エッジ対エッジ接触から消去されたセカンダリライン
