/INTER/TYPE24
ブロックフォーマットキーワード TYPE24は、ペナルティ法を使用した一般的な節点対サーフェスの接触インターフェースです。
ペナルティ剛性は一定であるため、時間ステップの影響は受けません(標準ペナルティ剛性の場合)。ソリッド要素にはゼロのギャップが割り当てられます。単一サーフェス、サーフェス対サーフェス、または節点対サーフェスという3種類の入力接触を定義できます。このインターフェースは、インターフェースTYPE3、TYPE5、またはTYPE7に代えて使用できます。陰解法の場合、このインターフェースTYPE24はSMPのみで使用できます。
フォーマット
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /INTER/TYPE24/inter_ID/unit_ID | |||||||||
| inter_title | |||||||||
| surf_ID1 | surf_ID2 | Istf | Irem_i2 | Idel | |||||
| grnd_IDs | Iedge | Edge_angle | Gap_max_s | Gap_max_m | |||||
| Stmin | Stmax | Igap0 | Ipen0 | Ipen_max | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| Stfac | Fric | Tstart | Tstop | ||||||
| IBC | Inacti | VISs | |||||||
| Ifric | Ifiltr | Xfreq | sens_ID | fric_ID | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| C6 | |||||||||
定義
| フィールド | 内容 | SI 単位の例 |
|---|---|---|
| inter_ID | インターフェースの識別子 (整数、最大10桁) |
|
| unit_ID | 単位識別子。 (整数、最大10桁) |
|
| inter_title | インターフェースのタイトル (文字、最大100文字) |
|
| surf_ID1 | 第1サーフェスの識別子 1 (整数) |
|
| surf_ID2 | セカンドサーフェスの識別子。 (整数) |
|
| Istf | インターフェース剛性定義フラグ 2 3
(整数) |
|
| Irem_i2 | インターフェースTYPE2で同じ接触ペア(節点 / セグメント)が定義されている場合に、セカンダリ節点を非アクティブにするためのフラグ。
|
|
| Idel | 節点およびセグメントの削除フラグ。
注: Idelを使用すると、CPUコストが高くなります。
|
|
| grnd_IDs | 節点グループの識別子 1 定義されている場合、節点グループはセカンダリ節点として追加されます。 (整数) |
|
| Iedge | エッジとエッジの接触のフラグ
(整数) |
|
| Edge_angle | エッジ角度 Iedge =1の場合のみ使用同じエッジを共有する2つのセグメント間の角度がEdge_angleの値より小さい場合、鋭角エッジがエッジ接触に含まれます。9 デフォルト = 135°(実数) |
|
| Gap_max_s | セカンダリの最大ギャップ。 4 デフォルト = 1030(実数) |
|
| Gap_max_m | メインの最大ギャップ。 4 デフォルト = 1030(実数) |
|
| Stmin | 最小剛性(Istf > 1かつIstf < 7の場合にのみ使用されます) 2 (実数) |
|
| Stmax | 最大剛性(Istf > 1かつIstf < 7の場合にのみ使用されます) 2 デフォルト = 1030(実数) |
|
| Igap0 | フリーエッジ上のセカンダリシェル節点のギャップ修正フラグ。
(整数) |
|
| Ipen0 | 初期貫通検出フラグ 8
(整数) |
|
| Ipen_max | 最大初期貫通 7 デフォルト = 0(実数) |
|
| Stfac | インターフェース剛性スケールファクター。 2 デフォルト = 1.0(実数) |
|
| Fric | Coulomb摩擦。 5 (実数) |
|
| Tstart | 開始時間。 9 (実数) |
|
| Tstop | 一時的な非アクティブ化の時間 9 デフォルト = 1030(実数) |
|
| IBC | 接触時の境界条件の非アクティブ化フラグ (ブーリアン) |
|
| Inacti | 初期貫通フラグ 7
(整数) |
|
| VISs | インターフェース剛性の臨界減衰係数 デフォルト = 0.05(実数) |
|
| Ifric | 摩擦定式化フラグ。 5 fric_IDが定義されていない場合のみ使用されます。
(整数) |
|
| Ifiltr | 摩擦フィルタリングフラグ。 6
(整数) |
|
| Xfreq | フィルタリング係数。 6 デフォルト = 1.0(実数) |
|
| sens_ID | インターフェースをアクティブ化 / 非アクティブ化するためのセンサーの識別子 9 (整数) |
|
| fric_ID | 選択されたパートのペアについての摩擦定義の摩擦識別子
(整数) |
|
| C1 | 摩擦則係数。 5 (実数) |
|
| C2 | 摩擦則係数。 (実数) |
|
| C3 | 摩擦則係数。 (実数) |
|
| C4 | 摩擦則係数。 (実数) |
|
| C5 | 摩擦則係数。 (実数) |
|
| C6 | 摩擦則係数。 (実数) |
境界条件の非アクティブ化フラグ: IBC
| (1)-1 | (1)-2 | (1)-3 | (1)-4 | (1)-5 | (1)-6 | (1)-7 | (1)-8 |
|---|---|---|---|---|---|---|---|
| IBCX | IBCY | IBCZ |
定義
| フィールド | 内容 | SI 単位の例 |
|---|---|---|
| IBCX | 衝撃時のX境界条件の非アクティブ化フラグ
(ブーリアン) |
|
| IBCY | 衝撃時のY境界条件の非アクティブ化フラグ
(ブーリアン) |
|
| IBCZ | 衝撃時のZ境界条件の非アクティブ化フラグ
(ブーリアン) |
コメント
- 接触メイン / セカンダリペアは以下の3つの方法で定義できます:
- 1つの自己接触サーフェスのみ: surf_ID1 > 0かつsurf_ID2 = 0
- 対称的なサーフェス対サーフェス: surf_ID1 > 0かつsurf_ID2 > 0
- 節点対サーフェス: grnd_IDs > 0、surf_ID1 = 0かつsurf_ID2 > 0
grnd_IDs > 0は、節点対サーフェス接触タイプを定義するために使用されますが、他の接触タイプでも使用できます。その場合、節点グループは、単純に補足的セカンダリ節点として追加されます。これは、ユーザーがスプリング要素節点、剛体のメイン節点などを接触に(セカンダリ節点として)追加する場合に役立ちます。
サーフェスがシェルを使用して定義されている場合は、反対の法線方向を持つ2つの接触セグメント(半分の板厚(t)でシフトされたもの)が生成されます: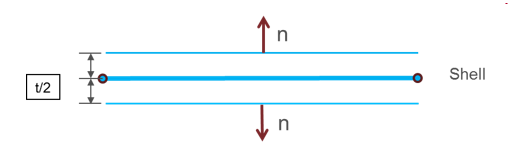
図 1.SPMDの場合、surf_IDi (i=1, 2)によって定義される各メインセグメントを1つの要素に関連付ける必要があります(ボイド要素の場合もあります)。
サーフェス定義/SURF/PART/ALLは、TYPE24では使用できません。
- 接触剛性Kは以下のように定義されます:
(1) ここで、 はIstfに依存- Istf = 1000の場合、 (デフォルトの剛性)
- Istf = 2、
- Istf = 3、
- Istf = 4、
- Istf = 5、
- Istf = 6、
、
柔らかい剛性。このオプションは陰解法のみで使用可能です。
各接点について、非線形反復収束をより簡単にするために、より小さい初期剛性が使用されます。接触パート(増大する貫通または反発を伴うもの)の反作用の関数用に剛性は調整されますが、常に入力剛性より小さなものになります。
- Istf = 12、Nitsche法:
- Istf = 13、Nitsche法:
- Istf = 14、Nitsche法:
: メインセグメントの剛性
- 、メインセグメントがシェル上にある場合
- 、メインセグメントがシェルとソリッドによって共有されている場合
- メインセグメントがソリッド上に存在する場合。
:セカンダリ節点剛性は、インターフェースTYPE24として考慮される相当節点剛性で、次のように計算されます:- 、節点がシェル要素に結合されている場合
- 、節点がソリッド要素に結合されている場合
ここで、- セグメント面積
- ソリッドの体積
- 体積弾性率
- シェルの板厚
Stfacの値は1.0より大きい値であることが可能です。剛性係数の値に制限はありません(値が1.0より大きいと、最初の時間ステップが短くなる場合があります)。
/PROP/VOIDと/MAT/VOIDを使用する際、ボイド材料の材料プロパティと板厚が入力されなければなりません。そうしないと、ボイド要素の接触合成はゼロになります。シェル要素の剛性が接触計算に使用されるため、これは、ボイドシェル要素がソリッド要素と要素を共有する場合に特に重要です。
陰解法解析が検討される場合(/IMPLICITで定義)、デフォルト値はIstf= 4ですが、弾性構造や曲げ主体の構造についてはIstf = 6が推奨されます。
- Nitsche法1は、接触方程式を解くために使用する接触アルゴリズムです。この手法は、従来のペナルティ接触法の代わりに使用できます。Nitsche法の方が、接触での貫通を防止できる点で優れています。特に、ゴムと金属との接触のように、材料剛性が異なるコンポーネントどうしの接触で効果的です。このようなケースでは、ペナルティ剛性の選択が困難です。最小の剛性を使用すると、大きい貫通が発生する可能性があり、最大の接触剛性を使用すると、要素が大きく変形して時間ステップが短くなる可能性があるからです。Nitsche法では、接触剛性、貫通、要素の応力を使用して接触力を計算するので、このような問題のモデル化を改善できます。Nitsche法は、ソリッド間の単一サーフェス接触またはサーフェス間接触にのみ使用でき、エッジ間接触には使用できません。
- ギャップは衝撃ごとに次のように自動計算されます(TYPE7のIgap = 1可変ギャップと同様):
(2) このとき、-
: メイン要素のギャップ:
、ここでtは、シェル要素に対するメイン要素の板厚
、3次元ソリッド要素の場合
-
: セカンダリ節点のギャップ:
、セカンダリ節点がどの要素にも結合されていないか、3次元ソリッド要素またはスプリング要素にのみ結合されている場合
、セカンダリ節点がシェル要素に接続されている場合。ここで、 は、セカンダリ節点に結合されているシェル要素の最大板厚
、セカンダリ節点がトラス要素またはビーム要素に結合されている場合。ここで、 は1次元要素の断面
セカンダリ節点が複数のシェルおよび/またはビームまたはトラスに結合されている場合は、計算された中で最も大きいセカンダリギャップが使用されます。
と は、ギャップの計算前にGap_max_mとGap_max_sによって別々に制限されます。
Igap0=1についての制限:
自由エッジ上のセカンダリシェル節点のギャップ修正フラグは、セカンダリ節点がオプションの節点グループ(grnd_IDs)で定義されている場合は何の影響も及ぼしません。
-
: メイン要素のギャップ:
- fric_IDが定義されている場合、接触摩擦は/FRICTIONで定義され、この入力カード内の摩擦入力(Ifric、C1など)使用されません。摩擦力は次のとおりです:
(3) このとき、粘着力は以下のように計算されます:
ここで、
ここで、 はクーロン摩擦で、以下のように定義されます:- フラグIfricの場合(デフォルト):
ここで (クーロン摩擦)
- フラグIfric > 1の場合、新しい摩擦モデルが導入されます。この場合、摩擦係数は次の関数によって設定されます:ここで、
- メインセグメントの垂直抗力の圧力
- メインセグメントに相対するセカンダリ節点の接線速度
現在は、係数C1~C6を使用して、新しい摩擦定式化の可変摩擦係数 を定義しています。
以下の定式化を使用できます:- Ifric = 1(汎用の粘性摩擦則):
(4) - Ifric = 2(修正Darmstad則):
(5) - Ifric = 3(Renard則):
の、
の、
の、
ここで、- 第1臨界速度 は、0以外にする必要があります( )。
- 第1臨界速度 は、第2臨界速度 より小さくする必要があります。
- 静止摩擦係数 と動摩擦係数 は、最大摩擦 より小さくする必要があります(( かつ )。
- 最小摩擦係数 は、静止摩擦係数 および動摩擦係数 より小さくする必要があります( かつ )。
表 1. 摩擦定式化の単位 Ifric Fric C1 C2 C3 C4 C5 C6 1 2 3
- フラグIfricの場合(デフォルト):
- 摩擦フィルタリングIfiltr = 1、2または3の場合は、接線力がフィルタを使用して以下のようにスムージングされます:
(6) ここで、α係数は、以下のように計算されます:- Ifiltr= 1の場合: α = Xfreq、単純な数値フィルター
- Ifiltr = 2の場合: 、標準の-3dBフィルターで、 、 はフィルタリング期間
- Ifiltr = 3の場合: 標準の-3dBフィルターで、Xfreqはカット周波数
フィルタリング係数Xfreqは、0~1の値にする必要があります。
- InactiおよびIpen_max、初期貫通の取り扱い:
- Inacti = 1000: 初期貫通が無視されます。接触力は加えられませんが、節点は接触から非アクティブ化されません。節点が接触しなくなり、後で接触し直した場合は、そのときに接触力が加えられます。
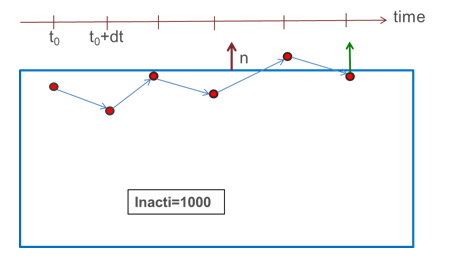
図 2. - Inacti = -1: 初期荷重はすべての貫通節点上に加えられます。高い初期貫通は回避する必要があります。これにより、大きな接触力が生じ、計算開始時に高エネルギーエラーとなる可能性があるからです。
初期貫通により生じる接触力は、t=0.0での0から10,000サイクルでのフル接触力に増加されます。この接触力の穏やかな増加により、モデル内の圧入状況のシミュレーションが可能となります。
- Inacti = 5: = 5: メインセグメントは初期貫通値( )でシフトされるため、時間0においては初期荷重は付与されません。
メインセグメントの位置が復元されるのは、 より大きい反発の場合のみです。
逆に、セカンダリ節点が引き続き貫通する場合は、貫通は以下のように計算されます:(7) 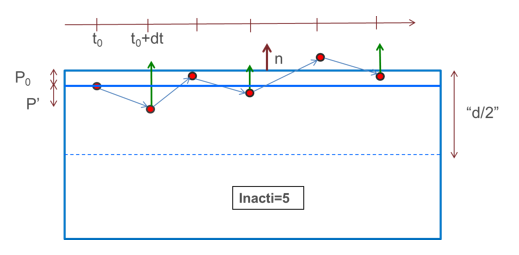
図 3.- 交差および大きい初期貫通(Inacti= -1および5):
シェルおよび厚いシェル: 初期交差は回避する必要があります。これにより、接触力方向に誤りが生じ、セカンダリ節点の固定につながる可能性があるからです。
ソリッド: デフォルトで、初期貫通の検索で考慮される距離は、以下のように計算されます:(8) このとき、各メインセグメントについて、- 結合されたソリッド要素の体積
- セグメント面積
- = 1~4)は、セグメントのエッジの長さ
- メインセグメントの数
- セグメントに結合しているソリッド要素の深さの予測(セグメントのサイズに制限されます)
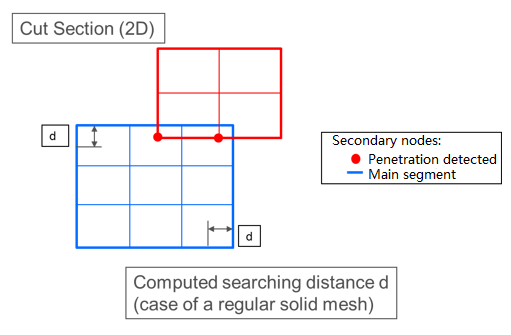
図 4.
最大初期貫通Ipen_max:- Ipen_maxに非ゼロの値が入力された場合、このデフォルト値は省略され、初期貫通がIpen_max内で検索されます。
- 検索距離に大きな値を入力すると、Radioss Starterのパフォーマンスが低下したり、メモリ割り当てエラーが発生する可能性があります。したがって、Ipen_maxに大きすぎる値を設定しないことが推奨されます。
- ただし、以下のように、Ipen_maxを使用して、計算された(デフォルトの)検索距離より大きい貫通を取得することができます(図 5参照):
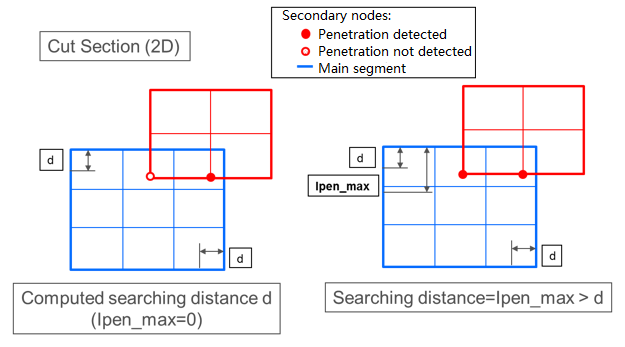
図 5.
- Inacti = 1000: 初期貫通が無視されます。接触力は加えられませんが、節点は接触から非アクティブ化されません。節点が接触しなくなり、後で接触し直した場合は、そのときに接触力が加えられます。
- Ipen0初期貫通検出フラグ
- デフォルトでは、各パート(シェル要素とソリッド要素のみ)の自己接触での貫通の検出は常に除外されます(surf_ID1が単独で定義され、Inacti =-1が設定されている場合でも同様です)。
- Ipen0 = 1 初期貫通は、各パートの自己接触で考慮され、初期荷重が設定されますが、一部の複雑な状況では、正しくない初期貫通が計算されることがあります。
- インターフェースのアクティブ化 / 非アクティブ化のためにsens_IDが定義されている場合、TstartおよびTstopは考慮されません。
- エッジ間接触が
=1を用いてアクティブ化される際、エッジ間接触は対称性で、接触に使用されるエッジは、定義されている単一サーフェス(surf_ID1)またはサーフェス間接触(surf_ID1とsurf_ID2)から自動的に生成されます:
- ソリッドおよびシェルの場合
エッジは、同じエッジを共有する2つの外部セグメント間の角度がEdge_angleの値(デフォルトでは135°)より小さいあらゆる箇所で考慮されます。
- シェルの場合エッジは、シェルパートの外周境界で考慮されます。
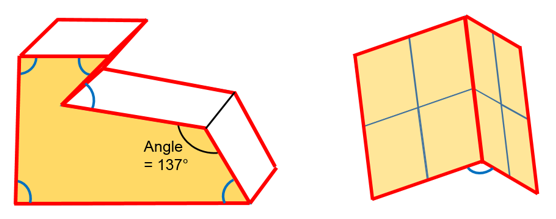
図 6.
- ソリッドおよびシェルの場合
- 出力される力について:
接触タイプが非対称的なサーフェス対サーフェスの場合、これら2つのサーフェスが適切に分離されていれば、時刻歴内の出力法線接触力が正しく計算されます。
- 陰解法について:
- インターフェースTYPE24はSMPのみで使用できます。
- Istfのデフォルトは4に設定されます(弾性構造や曲げ主体の構造に推奨されるIstf=6を使用できます)。
- Inactiのデフォルトは-1に設定されます。