/INTER/TYPE20 (Obsolete)

Edge to edge contact is also possible. Penalty stiffness is constant and therefore the time step is not affected (for standard penalty stiffness). This contact interface can replace interface TYPE3, TYPE5, TYPE7, TYPE11 or TYPE19. The interface is basically defined in terms of one or two surfaces. If only one surface is used, this surface is self-impacting. If two surfaces are defined, nodes of surface two impact surface one. A symmetric treatment can be activated. Edges of surface one and two can be taken into account for the contact. Nodes can be added to surface.

Format

Definitions

Flags for Deactivation of Boundary Conditions: IBC

Definitions

Comments

1. The simplest input is to enter only one self-impacting surface surf_ID₁. Symmetric treatment flag I_sym is used for node to surface contact but edge to edge contact is always symmetric.
2. To emulate an interface TYPE7 or TYPE11 input:

   TYPE20 to Emulate TYPE7 Input	TYPE20 to Emulate TYPE11 Input
   (TYPE20) surf_ID1 = surf_IDm (TYPE7) (TYPE20) grnd_ID = grnd_IDs (TYPE7)	(TYPE20) line_ID1 = line_IDs (TYPE11) (TYPE20) line_ID2 = line_IDm (TYPE11)
   (TYPE20) line_ID1 = 0 (TYPE20) line_ID2 = 0	(TYPE20) surf_ID1 = 0 (TYPE20) grnd_ID = 0
   (TYPE20) surf_ID2 = 0 (TYPE20) Isym = 2 (TYPE20) Iedge = 0	(TYPE20) surf_ID2 = 0 (TYPE20) Isym = 0 (TYPE20) Iedge = 0

3. In case of SPMD, each main segment defined by surf_ID_m must be associated to an element (possibly to a void element).
4. For the flag I_bag, refer to the monitored volume option (Monitored Volumes (Airbags)).
5. Flag I_del = 1 has a CPU cost higher than I_del = 2.
6. If I_gap = 0, a default value used for Gap_0, which is computed as:(1)
   $$Ga{p}_0=min\left(t,\frac{l}{10},\frac{l_{min}}{2}\right)$$
   With,

   t

   Average thickness of the main shell elements

   l

   Average side length of the main brick elements

   l_min

   Smallest side length of all main segments (shell or brick)

7. If I_gap = 1, the gap is computed for each impact as:
   (2)

   $$g_s+g_m$$
   With,

   • g_m: main element gap:

     $g_m=\frac{t}{2}$ , with t is the thickness of the main element for shell elements

     g_m = 0 for brick elements

   • g_s: secondary node gap:

     g_s = 0 if the secondary node is not connected to any element or is only connected to brick or spring elements.

     $g_s=\frac{t}{2}$ , with t is the largest thickness of the shell elements connected to the secondary node.

     $g_s=\frac{1}{2}\sqrt{S}$ for truss and beam elements, with S being the cross section of the element.

     If the secondary node is connected to multiple shells and/or beams or trusses, the largest computed secondary gap is used.

     If the free edge of a shell element is in contact, then I_gap can shift the gap of the free edges border shells, as:

     
     
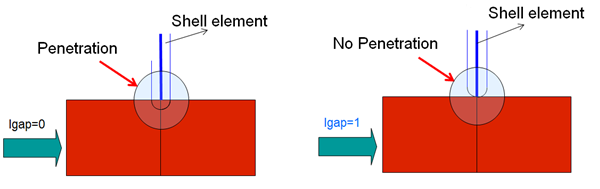
     Figure 1.

8. Deactivation of the boundary condition is applied to secondary nodes group (surf_ID_s).
9. Inacti = 3 may create initial energy if the node belongs to a spring element.
   Inacti = 5:

   
   
   Figure 2.

10. Maximum penetration value is set as a fraction of the actual gap (including variable gap):

    $Penetration\ge Fpenmax\cdot Gap$

    If the initial penetration of a secondary node is greater than the calculated maximum value (Fpenmax), the node will be deactivated from the interface (node stiffness deactivation).

11. One node can belong to the two surfaces at the same time.
12. There is no limitation value to the stiffness factor (but a value can be greater than 1.0 can reduce the initial time step).
13. For Friction Formulation:
    • If the friction flag is 0 (default), the old static friction formulation is used:

      $F_t\le \mu \cdot F_n$ with $\mu =\mathit{Fric}$ ( $\mu$ is Coulomb friction coefficient)

    • For flag I_fric > 0, new friction models are introduced. In this case, the friction coefficient is set by a function $\mu =\text{μ}(\rho ,V)$ ,
      Where,

      $\rho$

      Pressure of the normal force on the main segment

      $V$

      Tangential velocity of the secondary node

14. Currently, the coefficients C₁ through C₆ are used to define a variable friction coefficient $\mu$ for new friction formulations.
    The following formulations are available:

    • I_fric = 1 (Generalized viscous friction law):(3)
      $$\mu =\mathit{Fric}+C_1\cdot p+C_2\cdot V+C_3\cdot p\cdot V+C_4\cdot p^2+C_5\cdot V^2$$
    • I_fric = 2 (Modified Darmstad law):(4)
      $$\mu =Fric+C_1\cdot e^{\left(C_{2}V\right)}\cdot p^2+C_3\cdot e^{\left(C_{4}V\right)}\cdot p+C_5\cdot e^{\left(C_{6}V\right)}$$
    • I_fric = 3 (Renard law):

      $\mu =C_1+\left(C_3-C_1\right)\cdot \frac{V}{C_5}\cdot \left(2-\frac{V}{C_5}\right)$ if $V\in \left[0,C_5\right]$

      $\mu =C_3-\left(\left(C_3-C_4\right)\cdot {\left(\frac{V-C_5}{C_6-C_5}\right)}^2\cdot \left(3-2\cdot \frac{V-C_5}{C_6-C_5}\right)\right)$ if $V\in \left[C_5,C_6\right]$

      $\mu =C_2-\frac{1}{\frac{1}{C_2-C_4}+{\left(V-C_6\right)}^2}$ if $V\ge C_6$

      Where,

      $C_1={\mu }_s$ $C_2={\mu }_d$

      $C_3={\mu }_{\max }$ $C_4={\mu }_{\min }$

      $C_5=V_{\mathit{cr}1}$ $C_6=V_{cr2}$

    • First critical velocity $V_{cr1}=C_5$ must be different to 0 ( $C_5\ne 0$ ).
    • First critical velocity $V_{cr1}=C_5$ must be lower than the second critical velocity $V_{cr2}=C_6$ ( $C_5<C_6$ ).
    • The static friction coefficient $C_1$ and the dynamic friction coefficient $C_2$ , must be lower than the maximum friction $C_3$ ( $C_1\le C_3$ and $C_2\le C_3$ ).
    • The minimum friction coefficient $C_4$ , must be lower than the static friction coefficient $C_1$ and the dynamic friction coefficient $C_2$ ( $C_4\le C_1$ and $C_4\le C_2$ )
15. Friction filtering:
    If I_filtr ≠ 0, the tangential forces are smoothed using a filter:(5)

    $$F_t=\alpha \cdot {F^{\prime }}_t+\left(1-\alpha \right)\cdot {F^{\prime }}_t{}^{-1}$$
    Where, α coefficient is calculated from:

    • If I_filtr= 1 $\alpha =X_{\mathit{freq}}$ , simple numerical filter
    • If I_filtr = 2 $\alpha =\frac{2\cdot \pi }{X_{\mathit{freq}}}$ , standard -3dB filter, with $X_{\mathit{freq}}=\frac{dt}{T}$ , and T is filtering period
    • If I_filtr = 3 $\alpha =2\cdot \pi \cdot X_{freq}\cdot dt$ , standard -3dB filter, with X_freq is cutting frequency

      The filtering coefficient X_freq should have a value between 0 and 1.

16. Friction penalty formulation I_form
    • If I_form = 1, (default) viscous formulation, the friction forces are:(6)
      $$F_t=\min \left(\mu F_n,F_{adh}\right)$$

      While an adhesion force is computed as:

      $F_{adh}=C\cdot V_t$ with $C=VI{S}_F\cdot \sqrt{2Km}$

    • If I_form = 2, stiffness formulation, the friction forces are:(7)
      $$F_t^{new}=\min \left(\mu F_n,F_{adh}\right)$$

      While an adhesion force is computed as:

      $F_{adh}=F_t^{old}+\text{Δ}{F}_t$ with $\text{Δ}{F}_t=K\cdot V_t\cdot dt$

      Where, V_t is contact tangential velocity.