/MONVOL/FVMBAG (Obsolete)

Format

Definitions

Comments

1. surf_ID_ex must be defined using segments associated with 4-nodes or 3-nodes shell elements (possibly void elements).
2. The volume must be closed and the normals must be oriented outwards.
3. Abscissa scale factors are used to transform abscissa units in airbag functions, for example: (1)
   $$\text{F}(\text{t}\text{'})=\text{fct}\_\text{ID}\left(\frac{\text{t}}{{\text{Ascale}}_{\text{t}}}\right)$$
   where, t is the time. (2)

   $$\text{F}(\text{p}\text{'})=\text{fct}\_\text{ID}\left(\frac{\text{p}}{{\text{Ascale}}_{\text{p}}}\right)$$

   Where, p is the pressure.

4. The initial pressure is set to P_ext.
5. If ${\gamma }_i$ = 0, the characteristics of the gas initially filling the airbag are set to the characteristics of the gas by the first injector.
6. The gas flow in FVMBAG is solved using finite volumes.

   Some of these finite volumes can be entered by you through a group of solids, located inside the airbag and filling a part or the total internal volume. If there still exists a part of the internal volume which is not discretized by user-defined solids, an automatic meshing procedure produces the remaining volumes. This can be used for example to model a canister.

   A finite volume consists in a set of triangular facets. Their vertices do not necessarily coincide with the nodes of the airbag. The airbag envelope can be modeled with 4-node or 3-node membranes; however, 3-nodes are recommended.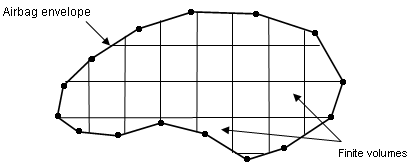

   
   
   Figure 1.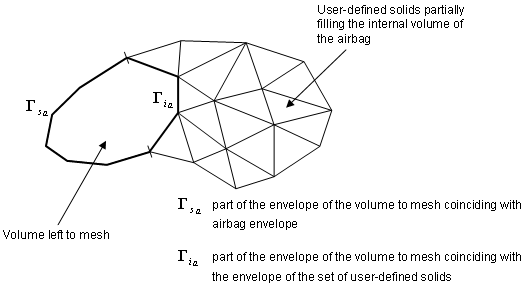

   
   
   Figure 2.

7. The exit velocity is given by:
   (3)

   $${\text{u}}^2=\frac{2\gamma }{\gamma -1}\frac{\text{P}}{\rho }\left(1-{\left(\frac{{\text{P}}_{\text{ext}}}{\text{P}}\right)}^{\frac{\gamma -1}{\gamma }}\right)$$
   The mass out flow rate is given by:(4)

   $${\dot{\text{m}}}_{\text{out}}={\rho }_{\text{v}}*\text{vent}\_\text{holes}\_\text{surface}*\text{u}$$
   The energy flow rate is given by:(5)

   $${\dot{\text{E}}}_{\text{out}}={\dot{\text{m}}}_{\text{out}}\frac{\text{E}}{\rho \text{V}}={\left(\frac{{\text{P}}_{\text{ext}}}{\text{P}}\right)}^{\frac{1}{\gamma }}*\text{vent}\_\text{holes}\_\text{surface}*\text{u}\frac{\text{E}}{\text{V}}$$
   The venting velocity is computed by:(6)

   $${\text{m}}_{\text{out}}=\rho *\text{vent}\_\text{holes}\_\text{surface}*\text{fct}\_{\text{ID}}_{\text{V}}*{\text{Fscale}}_{\text{V}}(\text{P}-{\text{P}}_{\text{ext}})$$
8. Vent hole membrane is deflated if T > T_vent or if the pressure exceeds P_def during more than $\text{Δt}{P}_{def}$ .
9. If surf_ID_v ≠ 0 (surf_ID_v is defined). (7)
   $$\text{vent}\_\text{holes}\_\text{surface}={\text{A}}_{\text{vent}}*{\text{fct}\_\text{ID}}_{\text{A}}(\text{A}/{\text{A}}_0)*{\text{fct}\_\text{ID}}_{\text{t}}(\text{t})*{\text{fct}\_\text{ID}}_{\text{P}}(\text{P}-{\text{P}}_{\text{ext}})$$

   Where, A is the Area of surface surf_ID and A₀ is the initial Area of surface surf_ID_v.

10. If surf_ID_v = 0 (surf_ID_v is not defined) vent hole is ignored.(8)
    $$\text{vent}\_\text{holes}\_\text{surface}={\text{A}}_{\text{vent}}*{\text{fct}\_\text{ID}}_{\text{t}}(\text{t})*{\text{fct}\_\text{ID}}_{\text{P}}(\text{P}-{\text{P}}_{\text{ext}})$$
11. Functions fct_ID_t and fct_ID_P are assumed to be equal to 1, if they are not specified (null identifier).
12. Function fct_ID_A is assumed as the fct_ID_A(A/A₀) = 1, if it is not specified.
13. Vent holes surface is computed as follows:(9)
    $$\begin{array}{ll}\text{vent}\_\text{holes}\_\text{surface}\hfill & {\text{=A}}_{\text{vent}}*{\text{A}}_{\text{non}\_\text{impacted}}*\text{fct}\_{\text{ID}}_{\text{t}}({\text{A}}_{\text{non}\_\text{impacted}}/{\text{A}}_0)*\text{fct}\_{\text{ID}}_{\text{P}}(\text{P}-{\text{P}}_{\text{ext}})\hfill \\ \hfill & +{\text{B}}_{\text{vent}}*{\text{A}}_{\text{impacted}}*\text{fct}\_{\text{ID}}_{{\text{t}}^{\prime }}({\text{A}}_{\text{impacted}}/{\text{A}}_0)*\text{fct}\_{\text{ID}}_{{\text{P}}^{\prime }}(\text{P}-{\text{P}}_{\text{ext}})\hfill \end{array}$$
    with impacted surface:(10)

    $${\text{A}}_{\text{impacted}}=\sum _{\text{e}\in {\text{S}}_{\text{vent}}}\frac{{\text{n}}_{\text{c}}\left(\text{e}\right)}{\text{n}\left(\text{e}\right)}{\text{A}}_{\text{e}}$$
    and non-impacted surface:(11)

    $${\text{A}}_{\text{non}\_\text{impacted}}=\sum _{\text{e}\in {\text{S}}_{\text{vent}}}\left(1-\frac{{\text{n}}_{\text{c}}\left(\text{e}\right)}{\text{n}\left(\text{e}\right)}\right){\text{A}}_{\text{e}}$$

    Where for each element e of the vent holes surf_ID_v, n_c(e) means the number of impacted nodes among the n(e) nodes defining the element.

    
    
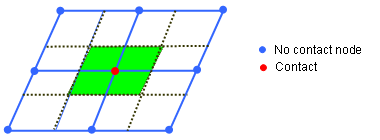
    Figure 3. From Nodes Contact to Impacted/Non-impacted Surface

14. Functions fct_ID_t' and fct_ID_P' are assumed to be equal to 1, if they are not specified (null identifier).
15. In order to use porosity during contact, flag I_BAG must be set to 1 in the interfaces concerned (Line 3 of interface Type 5 and Type 7). If not, the nodes impacted into the interface are not considered as impacted nodes in the previous formula for A_impacted and A_{non_impacted}.
16. Automatic finite volume meshing parameters.

    
    
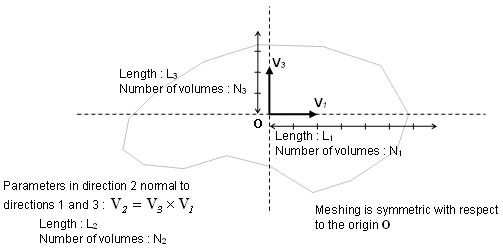
    Figure 4.

17. The finite volumes are generated in two steps.
    • The first step generates vertices lying exclusively on the envelope of the airbag. This allows to update the finite volume along with the deformation of the envelope and correspond to the following procedure (displayed in 2D for purpose of clarity):

      
      
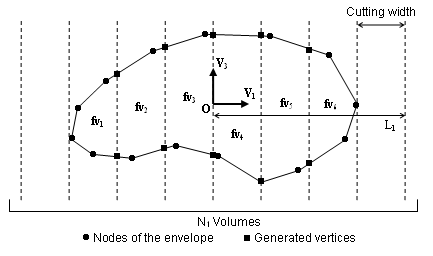
      Figure 5.

      This procedure requires the input of the direction V₃, named cutting direction, and of the direction V₁. A second direction V₂ in the plan normal to the cutting direction will be computed. In order to position the finite volumes and to determine the cutting width in both direction V₁ and V₂, an origin O must be provided as well as a length L_i, counted both positively and negatively from the origin, and a number of steps N_i. The cutting width is then given by W_i = 2L_i / N_i

      It is required that the box drawn in the horizontal plane (normal to V₃ ) by the origin O and the length L_i, counted both positively and negatively from O, includes the bounding-box of the envelope of the volume to mesh projected in this plane. This is necessary to ensure that this volume in entirely divided into finite volumes.

    • The second step performs horizontal cutting of the finite volumes, and may be useless in many cases of tightly folded airbags. It is especially required when injection is made in a canister filled by the injected gas before unfolding the airbag.
      This second step may generate vertices located inside the airbag. In order for them to be moved along with the inflation of the airbag, each is attached to a vertical segment (parallel to direction V₃) between two vertices lying on the envelope of the airbag (Figure 6). The local coordinates of the vertex within its reference segment remain constant throughout the inflation process.

      
      
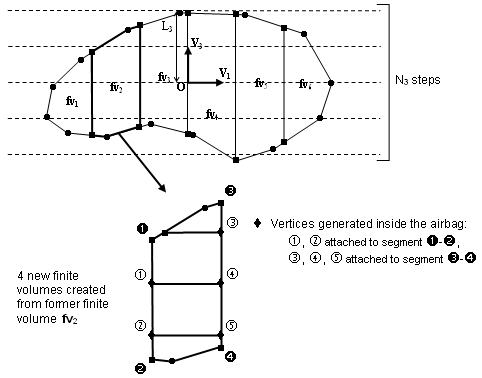
      Figure 6.

      The horizontal cutting width is given by W₃ = 2L₃ / N₃. It is not necessary that the segment given in the V₃ direction by the origin O and length L₃, counted both positively and negatively, includes the bounding-box of the envelope of the volume to mesh projection on the V₃ direction, since at the second step only existing finite volumes are cut.

18. Actual vector V₁ used for automatic meshing is obtained after orthogonalization of the input vector with respect to vector V₃.
19. When a finite volume fails during the inflation process of the airbag (volume becoming negative, internal mass or energy becoming negative), it is merged to one of its neighbors so that the calculation can continue. Two merging approaches are used:
    • Global merging: a finite volume is merged if its volume becomes less than a certain factor multiplying the mean volume of all the finite volumes. The flag Igmerg determines if the mean volume to use is the current mean volume (Igmerg =1) or the initial mean (Igmerg =2). The factor giving the minimum volume from the mean volume is Cgmerg.
    • Neighborhood merging: a finite volume is merged if its volume becomes less than a certain factor multiplying the mean volume of its neighbors. The factor giving the minimum volume from the mean volume is Cnmerg.
20. In the case of both Cgmerg and Cnmerg are not equal to 0, means both merging approach will be used simultaneously. In case of a strong shock, it is recommended to set q_a = 1.1 and q_b = 0.05.
21. When two layers of fabric are physically in contact, there should be no possible flow between finite volumes, which is numerically not the case because of interface gap. Hmin represents a minimum height for the triangular facets below which the facet is impermeable. Its value should be close to the gap of the self-impacting interface of the airbag.
22. Nlayer, Nfacmax, Nppmax are memory parameters that help the finite volume creation process. Changing their value cannot cause the calculation to stop. Increasing the leads to a higher amount of memory and a smaller computation time for automatic meshing.
23. During the finite volume creation process, plane polygons are first created, which are then assembled into closed polyhedra and decomposed into triangular facets. Nppmax is the maximum number of vertices of these polygons.
24. Iref set to 1 only works with a reference geometry based on /REFSTA (not yet supported if the reference geometry is based on /XREF) for monitored volumes types FVMBAG or FVMBAG1.
25. Only applicable to the Finite Volume Method, used to take internal surfaces or baffles into account as obstacles to the gas flow inside the monitored volume. Internal surfaces are taken into account in FVM only if the monitored volume is filled with solid elements, like TETRA4 (possibly HEXA and PENTA) with nodes coinciding with the monitored volume external and internal surface nodes (these solids must be declared in grbrick_ID). A porosity ranging from 0: no porosity up to 1: full porosity (vent) can be applied to internal surface fabrics only if their material model is LAW19. Injector surface can also be defined on an internal surface in which case the gas flow direction is opposite to the internal surface normal orientation.
26. If an element of a vent hole surface (surf_IDv) belongs to an injector (surf_IDinj) it will be ignored from the vent hole. A constant c correction factor f computed at time t=0 is applied to the total vent hole surface:(12)
    $$f=S_{\mathit{vent}}/(S_{\mathit{vent}}-S_{\mathit{injector}})$$