RD-E： 0300 S字型ビームの圧壊

S字型ビームが剛壁に対して初速度で圧壊されます。

圧壊荷重条件下でS字型ビームの感度の検討が行われます。このモデルは、Johnson-Cook弾塑性材料と、ビームの座屈をモデル化するためのペナルティ法に基づいた自動衝撃のセルフ接触インターフェースを使用しています。初速度が運動条件（剛体）を通じて左側の断面に与えられます。衝撃条件は滑りありで、右側断面の特定の境界条件を使ってモデル化されます。

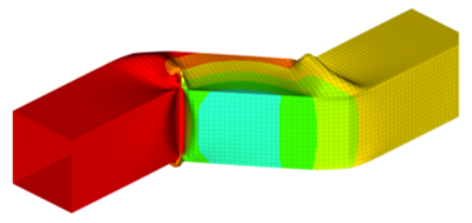
rad_ex3_s-beam
図 1.
3つの異なるパラメータが変化させられ、結果が比較されます：
  • シェル要素の定式化
    • BATOZ： Ishell=12
    • QEPH： Ishell=24
    • Q4 Belytschko： Ishell=3
  • シェル要素の5積分点vs全領域積分
  • 初速度の影響（5 m/sと10 m/s）
計算の比較にいくつかの基準が用いられます：
  • 変形形状
  • 圧壊力
  • 計算コスト
  • 運動エネルギー
  • 内部エネルギー

使用されるオプションとキーワード

入力ファイル

本例題で使用される入力ファイルは下記のとおり：
QEPH
<install_directory>/hwsolvers/demos/radioss/example/03_S-Beam/v_5ms/*
BATOZ
<install_directory>/hwsolvers/demos/radioss/example/03_S-Beam/global_IP/*
BT_type3
<install_directory>/hwsolvers/demos/radioss/example/03_S-Beam/v_10ms/*

モデル概要

S字型ビームが初速度 5 m/sで剛壁に対して圧壊されます。断面は、中空の正方形断面チューブ（それぞれの側部寸法は80mm）で、

板厚は1.5 mmです。チューブはスチール製で、塑性は考慮されますが破断は考慮されません。

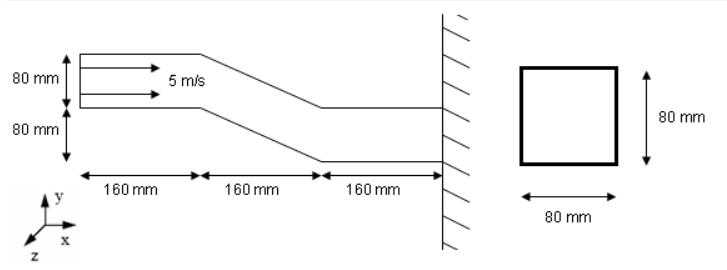
rad_ex_fig_3-1
図 2. 問題の概要とビームの断面

メッシュは規則的なシェルメッシュです。それぞれのシェルの寸法はおよそ5 mm x 5 mmです。

以下の単位系が用いられます： mm, ms, g, N, MPa

使用されている材料の特性は等方性弾塑性Johnson-Cook則に従います。
材料特性
ヤング率
199355 [ MPa ] MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWadaqaai Gac2eacaGGqbGaaiyyaaGaay5waiaaw2faaaaa@3BE6@
ポアソン比
0.3
密度
7.9x10-3 [ g m m 3 ] MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaamWaaeaada WcaaqaaiaadEgaaeaacaWGTbGaamyBamaaCaaaleqabaGaaG4maaaa aaaakiaawUfacaGLDbaaaaa@3BBC@
降伏応力
185.4 [ MPa ] MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWadaqaai Gac2eacaGGqbGaaiyyaaGaay5waiaaw2faaaaa@3BE6@
硬化パラメータ
540 [ MPa ] MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWadaqaai Gac2eacaGGqbGaaiyyaaGaay5waiaaw2faaaaa@3BE6@
硬化指数
0.32
最大応力
336.6 [ MPa ] MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWadaqaai Gac2eacaGGqbGaaiyyaaGaay5waiaaw2faaaaa@3BE6@

シミュレーションの反復

感度の検討が以下を比較して実行されます：
  • シェル要素の定式化：
    • BATOZ： Ishell=12 完全積分シェル要素、アワグラスなし
    • QEPH： Ishell=24 物理的なアワグラス安定化を伴う低減積分要素
    • Q4 Belytschko： Ishell=3 直交性を伴う弾塑性アワグラスありの低減積分要素
  • 厚み全体の積分法：
    • グローバル積分 (N=0)
    • 5積分点（N=5）
  • 初速度の影響：
    • 5 m/sおよび10 m/s


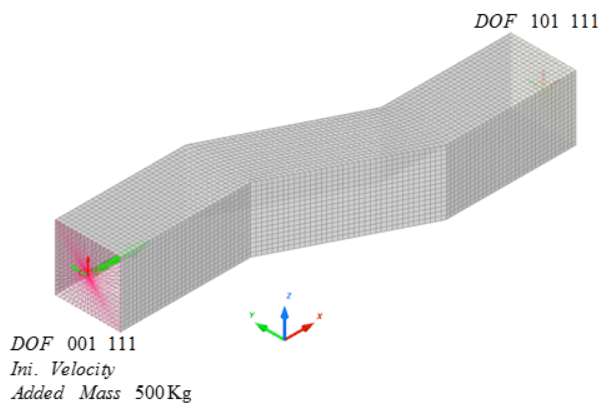
図 3. 構造の全体メッシュ

2つの剛体が右側と左側に生成されています。境界条件、速度および追加された質量が剛体に付与されています。

左側の断面は以下の条件に置かれます：
  • Z方向並進とX、Y、Z軸周り回転で固定
  • X方向に5 m/sの初速度
  • 500 Kgの質量が剛体の左端に付加されている

結果


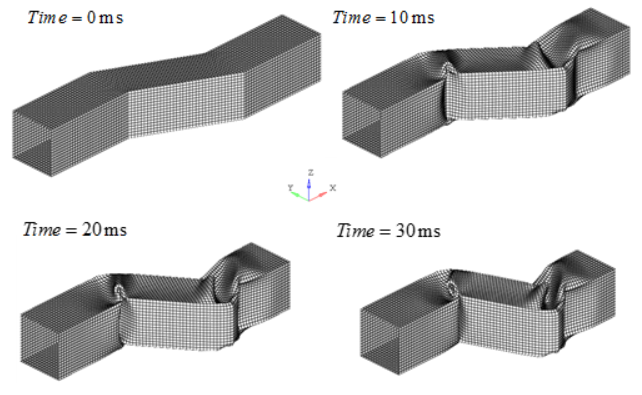
rad_ex_fig_3-4
図 4. QEPH定式化の変形後のメッシュ. （N=5、V=5 m/s）

N=5での異なるシェル定式化の影響

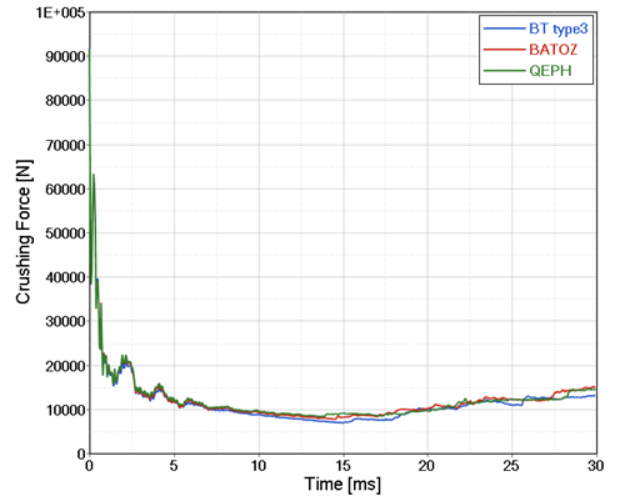
異なるシェル要素定式化は、圧壊力をわずかにのみ変化させます。塑性ひずみ結果も、これら3つのシェル要素定式化でほぼ同じです。計算コストに着目すると、QEPH要素は、完全積分BATOZ要素と比べて3倍速くなっています。Q4 TYPE3 Belytschko要素はQEPHと比べて1/3倍速くなりますが、Q4 BT TYPE3要素はアワグラスに対しより敏感であるため、通常QEPHが推奨されます。


図 5. 圧壊力vs異なるシェル定式化での変位DX. （N=5、V=5 m/s）


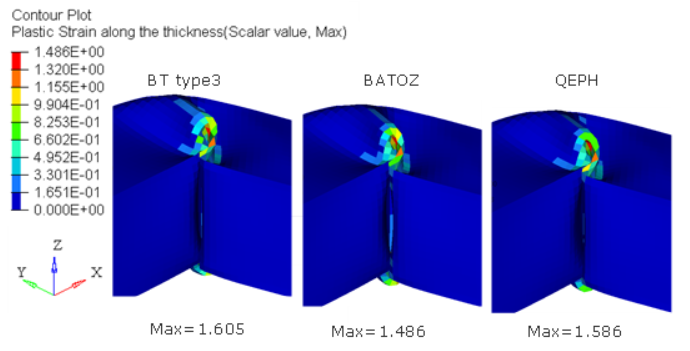
図 6. 異なるシェル定式化での塑性ひずみ. （N=5、V=5m/s）

異なる積分点の影響

表 1 は、グローバル積分（N=0）を使用したすべての要素の最大塑性ひずみが、板厚を貫通する5積分点（N=5）と比べて低過ぎる結果を戻すことを示しています。板厚を貫通する材料塑性を計算する際、より多くの積分点を使用すると精度は増しますが、計算負荷は高くなります。一般的にN=5が、計算速度と精度のバランス的に最良とされます。グローバル積分を用いることで計算速度は速まりますが、材料則1、2、22、36、43および60としか適合性がなく、破壊モデル（/FAIL）とは使用できません。詳細については、FAQ 材料 / 破断をご参照ください。
表 1. グローバル積分（N=0)、N=3およびN=5での計算コスト
    1 CPU

（正規化）

 最大塑性ひずみ
BT TYPE3

（Ishell=3）

 N=0 0.41 0.981
N=3 0.56 1.596
N=5 0.73 1.605
BATOZ

（Ishell=12）

 N=0 1.78 1.054
N=3 2.53 1.471
N=5 3.24 1.486
QEPH

（Ishell=24）

 N=0 0.65 0.958
N=3 0.78 1.516
N=5 1.00 1.586


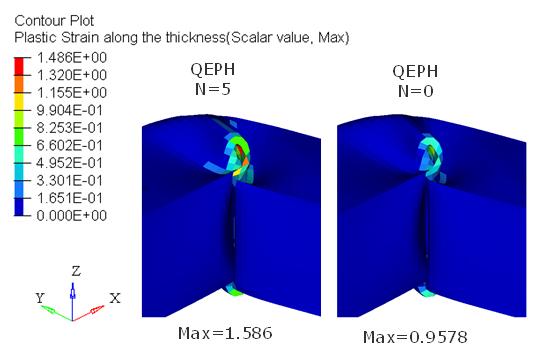
図 7. N=0とN=5でのQEPHの塑性ひずみ

初速度の影響

図 8 は、圧壊速度の影響（5 m/sと10 m/s）を示しています。この例題では、5積分点（N=5）でのQEPHシェル定式化（Ishell=24）を用いています。

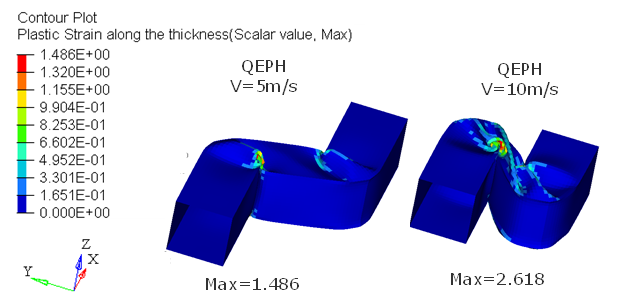
初速度が高いほど、初期運動エネルギーは大きく、その結果、ビームで変形と吸収エネルギーが大きくなります。


図 8. 異なる初速度での変形
表 2. 異なる速度でのエネルギー
  内部エネルギーIE

[mJ]

 運動エネルギー

[mJ]
V=5 m/s 1.674E+6

（係数1.0）

 4.574E+6

（係数1.0）
V=10 m/s 4.443E+6

（係数2.654）

 2.056E+7

（係数4.495）


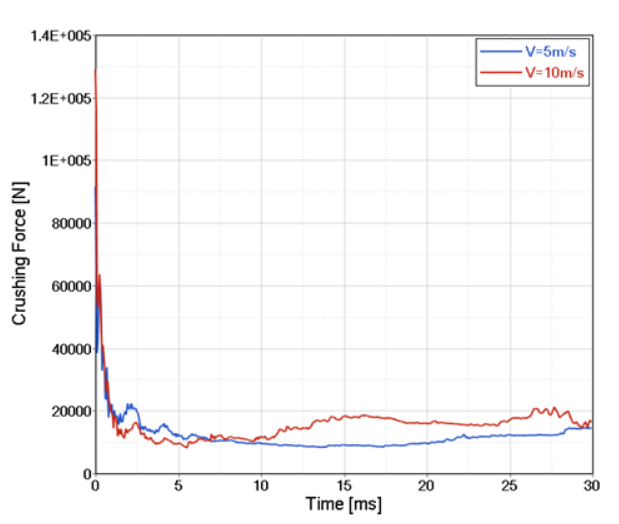
図 9. 異なる初速度に対する圧壊力対変位

まとめ

BATOZ（Ishell=12）と QEPH（Ishell=24）要素定式化で正確な結果が得られています。Q4 Belytschko（Ishell=3）要素は計算速度が速いものの、RD-E： 0100 ねじれた梁の例に示すように常にアワグラスが出現する可能性があります。Q4 Belytschko要素と比べ高価ではありますが、QEPH要素はアワグラスの問題はなく、更に高価である完全積分BATOZと非常に似通った結果を与えます。

グローバル積分（N=0）の使用は、計算速度は速いがN=5積分点の使用と比べ精確性で劣ります。グローバル積分の結果は塑性ひずみの過小評価を示し、限られた材料則としか使用できません。