/MAT/LAW24 (CONC)

An optional embedded model allows to take into account steel rebars into a homogenized model. Otherwise, rebars are usually meshed with 1D or 3D elements.

This material law is compatible with solid elements only.

Format

Definitions

Example (Concrete)

#RADIOSS STARTER
/UNIT/1
unit for mat
                   g                  mm                  ms
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/CONC/1/1
concrete - air dry
#              RHO_I
               .0024  
#                E_c                  NU      Icap
               41200                  .2         0
#                 fc            ft_on_fc            fb_on_fc            f2_on_fc            s0_on_fc
                  44                   0                   0                   0                   0
#                H_t               D_sup             EPS_max
                   0                   0                   0
#                k_y                 r_t                 r_c                H_bp
                   0                   0                   0                   0
#            ALPHA_y             ALPHA_F               V_max
                -0.2                -0.1                   0
#                f_k                 f_0                H_v0                eps0               h_fac
                   0                   0                   0
#                  E             sigma_y                 E_t
                   0                   0                   0
#             ALPHA1              ALPHA2              ALPHA3
                   0                   0                   0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

Comments

1. This material law can be used with only four parameters: ${\rho }_i,E_c,\nu$ and $f_c$ . Values $f_t,f_b,f_2,s_0$ are input as ratios of $f_c$ and are based on the failure of a typical concrete material.
2. The parameters for the damage model are:

   
   
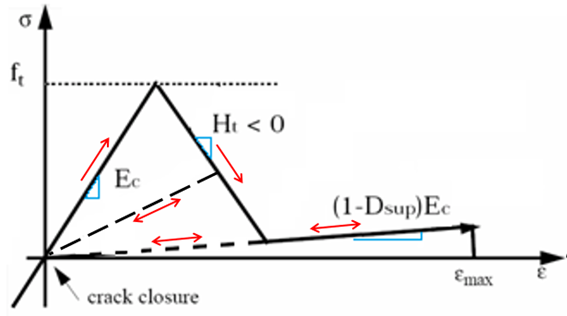
   Figure 1. Stress Strain Curve for LAW24 Damage Model. meridians of failure and yield surfaces

   Where, $f_c$ is the uniaxial compression strength.

3. The yield envelope is derived from the failure envelope using a scale factor $\mathrm{k}\left({\sigma }_m,k_0\right)$ .
   (1)

   $$f=r-\mathrm{k}\left({\sigma }_m,k_0\right)\cdot r_f=0$$
4. The scale factor $\mathrm{k}\left({\sigma }_m,k_0\right)$ is a function of mean stress (pressure), and $k_0$ is models the hardening effect. It is related to the surface where elasticity domain reaches its limit. In tension $\mathrm{k}\left({\sigma }_m,k_0\right)=1$ and the yield envelope and failure envelope are superimposed. In compression the scale factor $\mathrm{k}\left({\sigma }_m,k_0\right)$ depends on I_cap value (0, 1 or 2).

   
   
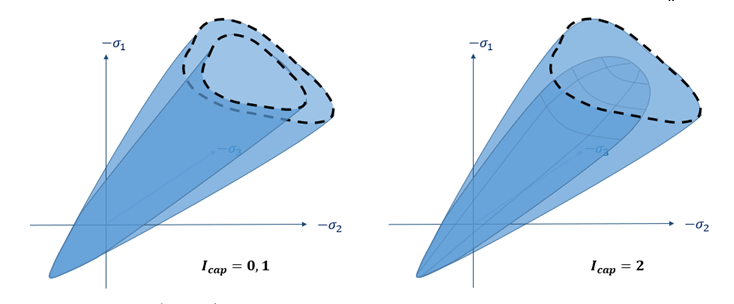
   Figure 2. Scale factor $\mathrm{k}\left({\sigma }_m,k_0\right)$ shapes the yield surface from the failure surface

   • For I_cap =0 or 1:

     
     
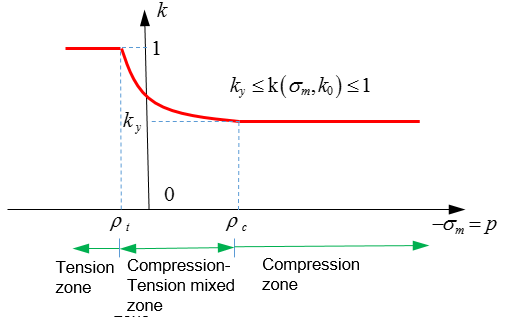
     Figure 3.

   • For I_cap =2 (with cap):

     
     
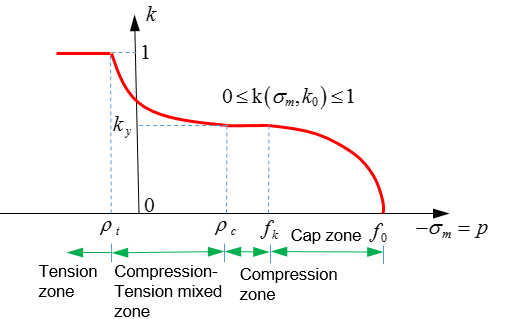
     Figure 4.

   Where, $r=\sqrt{2J_2}=\sqrt{\frac{2}{3}}{\sigma }_{VM}$ and ${\sigma }_m=\frac{I_1}{3}$ is mean stress (pressure), $I_1$ and $J_2$ are the first and second stress invariant.

5. There is no cap effect when ${\alpha }_y={\alpha }_f=0$ because there is no compaction. The default values of dilatancy parameters ${\alpha }_y$ and ${\alpha }_f$ were modified for I_cap = 0 or 2 in Radioss 2017. These parameters should be negative with recommended values of -0.2 and -0.1, respectively. The default cap formulation was updated in Radioss 2017. To enable the original cap formulation used in Radioss 14.0 and older, set I_cap = 1. The I_cap =2 formulation is more accurate for triaxial and hydrostatic loadings. The cap hardening is a function of the compaction coefficient. The shear hardening modulus is reduced in the transition region which assures better stability. I_cap = 2 must be used to output plastic strain using /ANIM/BRICK/EPSP or /H3D/SOLID/EPSP.
6. The embedded rebar model is optional. It uses an elastic-plastic with hardening material model. When defining rebar section fractions, a homogenized behavior is assumed for each element. The element should be large enough to stand for a Representative Elementary Volume (REV). This homogenized model is mostly used with large structures and a coarse mesh. Otherwise, rebar can be modeled with trusses, springs, beams, or even brick elements. the section ratio of rebars must be provided ${\alpha }_1$ , ${\alpha }_2$ , and ${\alpha }_3$ :

   
   
   Figure 5.

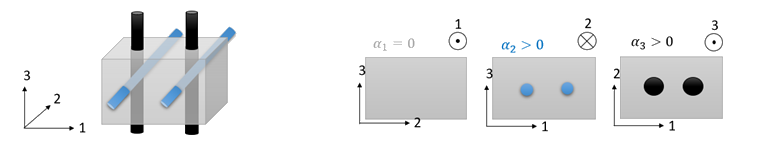
7. The rebar directions must be defined in the orthotropic solid property /PROP/TYPE6. Otherwise, the local element coordinate r, s, and t are taken respectively as directions 1, 2, and 3; unless I_solid = 1 or 2 is used with I_frame = 2; in which case the orthotropic directions 1, 2 and 3 are defined with the local co-rotating element coordinate r, s, and t, when time = 0.
8. In an axisymmetrical analysis, direction 3 is the $\theta$ direction.
9. The 10 node tetrahedron elements are compatible with this law.