/MAT/LAW113 (SPR_BEAM)

Deformation, force, and energy-based failure criteria are available. This material must be assigned to a /PART that references the spring property /PROP/TYPE23 (SPR_MAT).

Format

Loading index=1: Tension/Compression

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
K1		C1		A1		B1		D1
fct_ID11	H1	fct_ID21	fct_ID31	fct_ID41		${\delta }_{\min }^1$		${\delta }_{\max }^1$
F1		E1		Ascale1		Hscale1

Loading index=2: Shear XY

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
K2		C2		A2		B2		D2
fct_ID12	H2	fct_ID22	fct_ID32	fct_ID42		${\delta }_{\min }^2$		${\delta }_{\max }^2$
F2		E2		Ascale2		Hscale2

Loading index=3: Shear XZ

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
K3		C3		A3		B3		D3
fct_ID13	H3	fct_ID23	fct_ID33	fct_ID43		${\delta }_{\min }^3$		${\delta }_{\max }^3$
F3		E3		Ascale3		Hscale3

Loading index=4: Torsion

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
K4		C4		A4		B4		D4
fct_ID14	H4	fct_ID24	fct_ID34	fct_ID44		${\theta }_{\min }^4$		${\theta }_{\max }^4$
F4		E4		Ascale4		Hscale4

Loading index=5: Bending Y

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
K5		C5		A5		B5		D5
fct_ID15	H5	fct_ID25	fct_ID35	fct_ID45		${\theta }_{\min }^5$		${\theta }_{\max }^5$
F5		E5		Ascale5		Hscale5

Loading index=6: Bending Z

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
K6		C6		A6		B6		D6
fct_ID16	H6	fct_ID26	fct_ID36	fct_ID46		${\theta }_{\min }^6$		${\theta }_{\max }^6$
F6		E6		Ascale6		Hscale6

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
$v_0$		${\omega }_0$		Fcut		Fsmooth
c1		n1		${\alpha }_1$		${\beta }_1$
c2		n2		${\alpha }_2$		${\beta }_2$
c3		n3		${\alpha }_3$		${\beta }_3$
c4		n4		${\alpha }_4$		${\beta }_4$
c5		n5		${\alpha }_5$		${\beta }_5$
c6		n6		${\alpha }_6$		${\beta }_6$

Definitions

Example

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  1. LOCAL_UNIT_SYSTEM:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/2
units for material and property
                  Mg                  mm                   s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/PROP/SPR_MAT/26/2
SPOTWELD_NO_RUPTURE
#    Imass                        Volume             Inertia   skew_ID   sens_ID    Isflag     
         2                             1             6.55E-6         0         0         0     
/MAT/LAW113/26/2
SPOTWELD_NO_RUPTURE
                2E-6
#    Ifail     Ileng    Ifail2
                                   
#                 K1                  C1                  A1                  B1                  D1
              100000                   0                   0                   0                   0
# fct_ID11        H1  fct_ID21  fct_ID31  fct_ID41                    delta_min1          delta_max1
         1         1         0         0         0                             0               .5E-1
#                 F1                  E1             Ascale1             Hscale1
                   0                   0                   0                   0
#                 K2                  C2                  A2                  B2                  D2
              500000                   0                   0                   0                   0
# fct_ID12        H2  fct_ID22  fct_ID32  fct_ID42                    delta_min2          delta_max2
         2         1         0         0         0                        -.5E-1               .5E-1
#                 F2                  E2             Ascale2             Hscale2
                   0                   0                   0                   0
#                 K3                  C3                  A3                  B3                  D3
              500000                   0                   0                   0                   0
# fct_ID13        H3  fct_ID23  fct_ID33  fct_ID43                    delta_min3          delta_max3
         2         1         0         0         0                        -.5E-2               .5E-2
#                 F3                  E3             Ascale3             Hscale3
                   0                   0                   0                   0
#                 K4                  C4                  A4                  B4                  D4
             5000000                   0                   0                   0                   0
# fct_ID14        H4  fct_ID24  fct_ID34  fct_ID44                    delta_min4          delta_max4
         0         1         0         0         0                         -.015                .015
#                 F4                  E4             Ascale4             Hscale4
                   0                   0                   0                   0
#                 K5                  C5                  A5                  B5                  D5
             5000000                   0                   0                   0                   0
# fct_ID15        H5  fct_ID25  fct_ID35  fct_ID45                    delta_min5          delta_max5
         0         1         0         0         0                         -.015                .015
#                 F5                  E5             Ascale5             Hscale5
                   0                   0                   0                   0
#                 K6                  C6                  A6                  B6                  D6
             5000000                   0                   0                   0                   0
# fct_ID16        H6  fct_ID26  fct_ID36  fct_ID46                    delta_min6          delta_max6
         0         1         0         0         0                         -.015                .015
#                 F6                  E6             Ascale6             Hscale6
                   0                   0                   0                   0
#                 V0              Omega0               F_cut   Fsmooth
                   0                   0                   0         0
#                  C                   n               alpha                beta
                   0                   0                   0                   0
                   0                   0                   0                   0
                   0                   0                   0                   0
                   0                   0                   0                   0
                   0                   0                   0                   0
                   0                   0                   0                   0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  7. FUNCTIONS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/1
spotweld tensile function                                                                           
#                  X                   Y
              -250.0             -8250.0
               -0.25             -8250.0
                 0.0                 0.0
                0.25              8250.0
               250.0              8250.0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/2
Spotweld shear function                                                                             
#                  X                   Y
              -250.0            -25000.0
               -0.25            -25000.0
                 0.0                 0.0
                0.25             25000.0
               250.0             25000.0
#enddata

Comments

1. When used with /PROP/TYPE23 (SPR_MAT), this material law has the same behavior as spring property /PROP/SPR_BEAM.
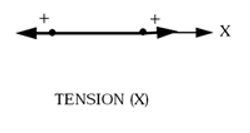
2. Inputs repeated for each degree of freedom (DOF) $i$ are defined with the following directions:
   • $i$ =1: tension/compression
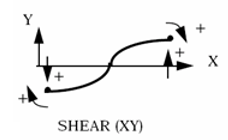
   • $i$ =2: shear xy
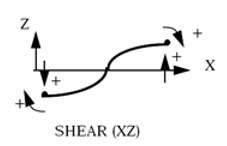
   • $i$ =3: shear xz
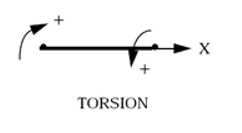
   • $i$ =4: torsion
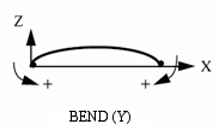
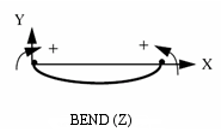
   • $i$ =5: bending y
   • $i$ =6: bending z
3. The spring's $X$ direction is defined using nodes N1 and N2 of the spring.
   If the node of the spring N3 is defined, the spring's $Y^{\prime }$ direction is defined using nodes N1 and N3 of the spring. N3, N2, and N1 should not be in a line.

   
   
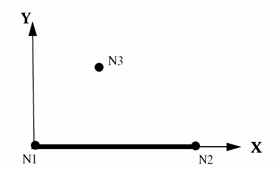
   Figure 1.

   • The $Z$ direction is:(1)
     $$\mathbf{Z}=\mathbf{X}\Lambda {\mathbf{Y}}^{\prime }$$
   • If node N3 is not defined in the element input, and skew system is defined in the /PROP/TYPE23 (SPR_MAT) input, the $Z$ direction is:(2)
     $$\mathbf{Z}=\mathbf{X}\Lambda {\mathbf{Y}}_{\mathit{skew}}$$
   • If neither node N3 nor skew system are defined in input, the $Z$ direction is:(3)
     $$\mathbf{Z}=\mathbf{X}\Lambda {\mathbf{Y}}_{\mathit{global}}$$

   Except when the spring local $X$ direction and $Y_{global}$ are colinear then:(4)

   $$\mathbf{Z}=\mathbf{X}\Lambda {\mathbf{X}}_{\mathit{global}}$$
   Finally, $Y$ direction is found as:(5)

   $$\mathbf{Y}=\mathbf{Z}\Lambda \mathbf{X}$$
4. If I_leng = 1, the spring stiffness properties are related on the initial spring length. The input should be entered as:

   $K=k*l_0$

   $C=c*l_0$

   Each spring will then have the following properties in the model:

   $k=\frac{K}{l_0}$

   $c=\frac{C}{l_0}$

   Where,

   $K$ and $C$

   Spring values entered in the spring property fields

   $k$ and $c$

   Spring’s actual physical mass, inertia, stiffness and damping

   $l_0$

   Initial spring length which is the distance between node N1 and N2 of the spring

   ${\delta }_{\min }^1\text{ and }{\delta }_{\max }^1$

   Failure values entered as engineering strain

5. Force and moment computation. For additional information, refer to Stiffness Formulation in the User Guide.

   If I_leng = 0, translational DOFs $i$ =1,2,3 - use displacement to determine spring forces and use rotational angle in radians for rotational DOFs $i$ =4,5,6 to determine spring moments.

   The values of forces and moments in the spring are computed as:

   • Linear spring:

     $\mathrm{F}\left(\delta \right)=K_i{\delta }^i+C_i{\dot{\delta }}^i$ with $i$ =1,2,3

     $\mathrm{M}\left(\theta \right)=K_i{\theta }^i+C_i{\dot{\theta }}^i$ with $i$ =4,5,6

   • Nonlinear spring:

     $\mathrm{F}\left(\delta \right)=\mathrm{f}\left(\frac{{\delta }^i}{Ascal{e}_i}\right)\left[A_i+B_i\ln \left|\frac{{\dot{\delta }}^i}{D_i}\right|+E_i\mathrm{g}\left(\frac{{\dot{\delta }}^i}{F_i}\right)\right]+C_i{\dot{\delta }}^i+Hscal{e}_i\mathrm{h}\left(\frac{{\dot{\delta }}^i}{F_i}\right)$ with $i$ =1,2,3

     $\mathrm{M}\left(\theta \right)=\mathrm{f}\left(\frac{{\theta }^i}{Ascal{e}_i}\right)\left[A_i+B_i\ln \left|\frac{{\dot{\theta }}^i}{D_i}\right|+E_i\mathrm{g}\left(\frac{{\dot{\theta }}^i}{F_i}\right)\right]+C_i{\dot{\theta }}^i+Hscal{e}_i\mathrm{h}\left(\frac{{\dot{\theta }}^i}{F_i}\right)$ with $i$ =4,5,6

     Where,

     • ${\delta }^i$ (with $-l_0<{\delta }^i<+\infty$ ) is the difference between the current length $l$ and the initial length $l_0$ of the spring element for corresponding translational DOF.
     • ${\theta }^i$ is the relative angle for corresponding rotational DOF in radians.
     • For linear springs, $\mathrm{f}\left(\delta \right),\text{}\mathrm{g}\left(\dot{\delta }\right)$ and $\mathrm{h}\left(\dot{\delta }\right),\left(\mathrm{f}\left(\theta \right),\mathrm{g}\left(\dot{\theta }\right)\text{and}\mathrm{h}\left(\dot{\theta }\right)\right)$ are zero functions and $A_i$ , $B_i$ , $E_i$ and $Hscal{e}_i$ are not taken into account.
     • If stiffness function $\mathrm{f}\left(\delta \right)$ or $\mathrm{f}\left(\theta \right)$ is requested, then $K$ is used as a slope for unloading only.
     • If $K$ is lower than the maximum slop of function $\mathrm{f}\left(\delta \right)$ or $\mathrm{f}\left(\theta \right)$ ( $K$ is not consistent with the maximum slope of the curve), $K$ is set to the maximum slope of the curve.

   If I_leng = 1, translational DOFs $i$ =1,2,3 - use engineering strain (elongation per unit length) to determine spring forces and use rotational per unit length for rotational DOFs $i$ =4,5,6 to determine spring moments. Spring parameters are related to initial spring length.

   The forces and moments in the spring are computed as:

   • $\mathrm{F}\left(\epsilon \right)=\mathrm{f}\left(\frac{{\epsilon }^i}{Ascal{e}_i}\right)\left[A_i+B_i\ln \left(\max \left(1,\left|\frac{{\dot{\epsilon }}^i}{D_i}\right|\right)\right)+E_i\mathrm{g}\left(\frac{{\dot{\epsilon }}^i}{F_i}\right)\right]+C_i{\dot{\epsilon }}^i+Hscal{e}_i\mathrm{h}\left(\frac{{\dot{\epsilon }}^i}{F_i}\right)$ with $i$ =1,2,3
   • $\mathrm{M}\left(\frac{\theta }{l_0}\right)=\mathrm{f}\left(\frac{{\frac{\theta }{l_0}}^i}{Ascal{e}_i}\right)\left[A_i+B_i\ln \left(\max \left(1,\left|\frac{{\frac{\dot{\theta }}{l_0}}^i}{D_i}\right|\right)\right)+E_i\mathrm{g}\left(\frac{{\frac{\dot{\theta }}{l_0}}^i}{F_i}\right)\right]+C_i{\frac{\theta }{l_0}}^i+Hscal{e}_i\mathrm{h}\left(\frac{{\frac{\dot{\theta }}{l_0}}^i}{F_i}\right)$ with $i$ =4,5,6
   Where,

   ${\epsilon }^i=\frac{{\delta }^i}{l_0}$

   Engineering strain

   $\frac{\theta }{l_0}$

   Rotation divided by the original spring length

6. Time step calculation.
   • Time step for translational DOF is computed as:(6)
     $$\text{Δ}{t}_i=\frac{\sqrt{M\cdot \max (K_i)+C_i{}^2}-C_i}{\max (K_i)}$$

     with $i$ =1, 2, 3

   • Time step for rotational DOF is computed as:(7)
     $$\text{Δ}{t}_i=\frac{\sqrt{I\cdot \max (K{\text{'}}_i)+{{C\text{'}}_i}^2}-C{\text{'}}_i}{\max (K{\text{'}}_i)}$$

     with $i$ =4, 5, 6

   Where,

   $K{\text{'}}_i=\max (K_t)\cdot L^2+\max (K_i)$

   $C{\text{'}}_i=\max (C_t)\cdot L^2+\max (C_i)$

   with $i$ =1, 2, 3 and $i$ =4, 5, 6 and $\text{min}\left(\text{Δ}{t}_i\right)$ is used as spring time step.

7. Failure criteria:
   • For uni-directional failure criteria I_fail=0, the spring fails as soon as one of the criteria is met in one direction:(8)
     $${\alpha }_i\left(\frac{{\delta }^i}{{\delta }_{\max }^i}\right)\ge 1$$
     or(9)

     $${\alpha }_i\left|\frac{{\delta }^i}{{\delta }_{\min }^i}\right|\ge 1$$
     with ${\delta }_{\max }^i$ and ${\delta }_{\min }^i$ being the failure limits in direction $i$ =1,2,3(10)

     $${\alpha }_i\left(\frac{{\theta }^i}{{\theta }_{\max }^i}\right)\ge 1$$
     or(11)

     $${\alpha }_i\left|\frac{{\theta }^i}{{\theta }_{\min }^i}\right|\ge 1$$

     with ${\theta }_{\max }^i$ and ${\theta }_{\min }^i$ being the failure limits in direction $i$ =4,5,6

     For each direction ${\delta }_{\min }^i$ (or ${\theta }_{\min }^i$ ) should be negative and ${\delta }_{\max }^i$ (or ${\theta }_{\max }^i$ ) should be positive. If the values are zero, then no failure will be considered.

   • For multi-directional failure criteria I_fail=1, the spring fails when the following criteria is fulfilled:(12)
     $${{\displaystyle \sum _{i=1,2,3}{\alpha }_i\left(\frac{{\delta }^i}{{\delta }_{fail}^i}\right)}}^{{\beta }_i}+{{\displaystyle \sum _{i=4,5,6}{\alpha }_i\left(\frac{{\theta }^i}{{\theta }_{fail}^i}\right)}}^{{\beta }_i}\ge 1$$
     • For "old" displacement formulation (I_fail2 = 0), the coefficients ${\alpha }_i$ and ${\beta }_i$ are equal to 1.0 and 2.0, respectively.
     • The new displacement formulation (I_fail2 =1) allows to model velocity dependent failure limit for translational DOF:(13)
       $${\delta }_{fail}^i=\{\begin{array}{c}{\delta }_{\max }^i+c_i\cdot {\left|\frac{v^i}{v_0}\right|}^{ni},if\left({\delta }^i>0\right)\\ {\delta }_{\min }^i-c_i\cdot {\left|\frac{v^i}{v_0}\right|}^{ni},if\left({\delta }^i\le 0\right)\end{array}$$
       with $i$ =1,2,3(14)

       $${\theta }^i{}_{fail}=\{\begin{array}{c}{\theta }_{\max }^i+c_i\cdot {\left|\frac{{\omega }^i}{{\omega }_0}\right|}^{ni},if\left({\theta }^i>0\right)\\ {\theta }_{\min }^i-c_i\cdot {\left|\frac{{\omega }^i}{{\omega }_0}\right|}^{ni},if\left({\theta }^i\le 0\right)\end{array}$$

       with $i$ =4,5,6

       Where, ${\delta }_{\min }^i$ or ${\delta }_{\max }^i$ is the static displacement failure limit (Lines 5, 8 and 11), and ${\nu }_0$ is the reference velocity.

       Where, ${\theta }_{\min }^i$ or ${\theta }_{\max }^i$ is the static rotation failure limit (Lines 14, 17 and 20), and ${\omega }_0$ is the reference velocity.

       Relative velocity coefficients, $c_i$ (with $i$ =1,2,3) have the units of displacement and $c_i$ (with $i$ =4,5,6) have the units of rotation.

     • Force or moment failure criteria is activated with I_fail2=2:(15)
       $${\delta }^i{}_{fail}=\{\begin{array}{c}{\delta }_{\max }^i+c_i\cdot {\left|\frac{v^i}{v_0}\right|}^{ni},if\left({\delta }^i>0\right)\\ {\delta }_{\min }^i-c_i\cdot {\left|\frac{v^i}{v_0}\right|}^{ni},if\left({\delta }^i\le 0\right)\end{array}$$
       with $i$ =1,2,3 for force criteria(16)

       $${\theta }^i{}_{fail}=\{\begin{array}{c}{\theta }_{\max }^i+c_i\cdot {\left|\frac{{\omega }^i}{{\omega }_0}\right|}^{ni},if\left({\theta }^i>0\right)\\ {\theta }_{\min }^i-c_i\cdot {\left|\frac{{\omega }^i}{{\omega }_0}\right|}^{ni},if\left({\theta }^i\le 0\right)\end{array}$$

       with $i$ =4,5,6 for moment criteria

       Where, ${\delta }_{\min }^i$ or ${\delta }_{\max }^i$ is the static failure limit force (Lines 5, 8, and 11) and ${\nu }_0$ is the reference velocity.

       Where, ${\theta }_{\min }^i$ or ${\theta }_{\max }^i$ is the static failure limit moment (Lines 14, 17 and 20), and ${\omega }_0$ is the reference velocity.

       Relative velocity coefficients, $c_i$ (with $i$ =1,2,3) have the units of force and $c_i$ (with $i$ =4,5,6) have the units of momentum.

     • Energy failure criteria is activated with I_fail2= 3:(17)
       $${\delta }^i{}_{fail}={\delta }_{\max }^i+c_i\cdot {\left|\frac{v^i}{v_0}\right|}^{ni},if\left({\delta }^i>0\right)$$

       with $i$ =1,2,3

       (18)

       $${\theta }^i{}_{fail}={\theta }_{\max }^i+c_i\cdot {\left|\frac{{\omega }^i}{{\omega }_0}\right|}^{ni},if\left({\theta }^i>0\right)$$

       with $i$ =4,5,6

       Where, ${\delta }_{\max }^i$ is the static failure limit translational energy (Lines 5, 8, and 11) and ${\nu }_0$ is the reference velocity.

       Where, ${\theta }_{\max }^i$ is the static failure limit rotational energy (Lines 14, 17 and 20), and ${\omega }_0$ is the reference velocity.

       In this case, the displacement values are replaced by positive failure energy values and the rotation values are replaced by positive failure energy values.

       Relative velocity coefficients, $c_i$ have the units of energy.

8. Spring elements with sensor activation or deactivation are mainly used in the pretension models.