/MAT/LAW32 (HILL)
Block Format Keyword This law describes the Hill orthotropic plastic material. It is applicable only to shell elements. This law differs from LAW43 (HILL_TAB) only in the input of yield stress.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /MAT/LAW32/mat_ID/unit_ID or /MAT/HILL/mat_ID/unit_ID | |||||||||
| mat_title | |||||||||
| E | |||||||||
| a | n | ||||||||
| m | |||||||||
| r00 | r45 | r90 | Iyield0 | ||||||
Definitions
| Field | Contents | SI Unit Example |
|---|---|---|
| mat_ID | Material identifier. (Integer, maximum 10 digits) |
|
| unit_ID | Unit Identifier. (Integer, maximum 10 digits) |
|
| mat_title | Material title. (Character, maximum 100 characters) |
|
| Initial density. (Real) |
||
| E | Young's modulus. (Real) |
|
| Poisson's ratio. (Real) |
||
| a | Yield parameter. (Real) |
|
| Hardening parameter. (Real) |
||
| n | Hardening exponent. (Real) |
|
| Failure plastic strain. Default = 1030 (Real) |
||
| Maximum stress. Default = 1030 (Real) |
||
| Minimum strain rate. Default = 1.0 (Real) |
||
| m | Strain rate exponent. Default = 0.0 (Real) |
|
| r00 | Lankford parameter 0 degree. 5
Default = 1.0 (Real) |
|
| r45 | Lankford parameter 45 degrees. Default = 1.0 (Real) |
|
| r90 | Lankford parameter 90 degrees. Default = 1.0 (Real) |
|
| Iyield0 | Yield stress flag.
(Integer) |
Example (Steel)
#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
kg mm ms
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/HILL/1/1
void_steel
# RHO_I
7.8E-7
# E NU
210 .3
# A EPSILON_0 n EPS_max SIGMA_max
.17 .2 .45 0 0
# EPS_DOT_0 m
0 0
# r00 r45 r90 Iyield0
.75 1 1.25 0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
Comments
- The yield stress is defined as
follows:
(1) The elastic limit is given by:(2) Where,- Plastic strain
- Strain rate
- The yield stress is compared to the
equivalent stress:
(3) 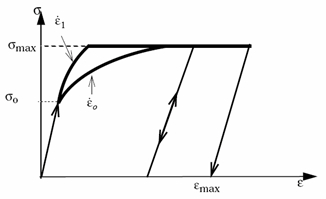
Figure 1. - This material law must be used with property set type /PROP/TYPE10 (SH_COMP) or /PROP/TYPE9 (SH_ORTH).
- Iterative projection (Iplas =1) and radial return (Iplas =2) for shell plane stress plasticity are available.
- Angles for Lankford parameters are
defined with respect to orthotropic direction 1.
(4) The Lankford parameters rα is the ratio of plastic strain in plane and plastic strain in thickness direction .(5) Where, α is the angle to the orthotropic direction 1.
This Lankford parameters rα could be determined from a simple tensile test at an angle α.
A higher value of R means better formability.
- If the yield stresses have been obtained in the orthotropic direction 1, define Iyield0 =1; otherwise Iyield0 =0.
- When reaches the value of , in one integration point, then the corresponding shell element is deleted.