/MAT/LAW83
Block Format Keyword This law describes the Connection material, which can be used to model spotweld, welding line, glue, or adhesive layers in laminate composite material.
Elastic and elastoplastic behavior can be defined. The plastic behavior of the material can be coupled in normal and shear directions for corresponding displacement-rates. This material is applicable only to solid hexahedron elements (/BRICK) and the material time-step does not depend on element height.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /MAT/LAW83/mat_ID/unit_ID | |||||||||
| mat_title | |||||||||
| E | G | Imass | |||||||
| fct_ID1 | Y_scale1 | X_scale1 | α | ||||||
| RN | RS | Fsmooth | Fcut | ||||||
| fct_IDN | fct_IDS | XSCALE | |||||||
Definitions
| Field | Contents | SI Unit Example |
|---|---|---|
| mat_ID | Material
identifier (Integer, maximum 10 digits) |
|
| unit_ID | Unit Identifier (Integer, maximum 10 digits) |
|
| mat_title | Material
title (Character, maximum 100 characters) |
|
| Initial
density (Real) |
||
| E | Young's (stiffness)
modulus per unit length. (Real) |
|
| G | Shear (stiffness) modulus
per unit length. Default = E (Real) |
|
| Imass | Mass calculation flag.
(Integer) |
|
| fct_ID1 | Normalized yield curve
that specifies true stress vs. plastic
displacement. (Integer) |
|
| Y_scale1 | Scale factor for ordinate
of the normalized function, fct_ID1. 10 Default = 1.0 (Real) |
|
| X_scale1 | Scale factor for abscissa
of the function, fct_ID1. 10 Default = 1.0 (Real) |
|
| α | Angle parameter used in
the calculation of the effective true stress. 8 Default = 0.0 (Real) |
|
| Exponent used in the
calculation of the effective true stress. 8 Default = 2.0 (Real) |
||
| RN | Maximum true stress in
normal direction used in the calculation of effective true
stress. Default = 1.0 (Real) |
|
| RS | Maximum true stress in
shear direction used in the calculation of effective true
stress. Default = 1.0 (Real) |
|
| Fsmooth | Displacement rate
filtering flag.
(Integer) |
|
| Fcut | Cutoff frequency for the
displacement rate filtering. Default = 1030 (Real) |
|
| fct_IDN | Function identifier
defining a scale factor vs. the plastic displacement rate in normal
direction. 9 Default = 0 (Integer) |
|
| fct_IDS | Function identifier
defining a scale factor vs. the plastic displacement rate in shear
direction. 9 Default = 0 (Integer) |
|
| XSCALE | Scale factor for the
abscissa of functions
fct_IDN and
fct_IDS. 9 Default = 1.0 (Real) |
Example (Connect)
#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
kg mm ms
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW83/1/1
CONNECT MATERIAL
# RHO_I
7.8E-6
# E G Imass
20 0
# Fct_ID1 Y_scale1 X_scale1 ALPHA BETA
200 1 1 0 2
# RN RS Fsmooth Fcut
.2 .4 0 0
# Fct_IDN Fct_IDS XSCALE
0 0 0
/FAIL/SNCONNECT/1/1
# ALPHA_0 BETA_0 ALPHA_F BETA_F Ifail_so ISYM
0 2 0 2 1 1
# Fct_0N Fct_0S Fct_FN Fct_FS XSCALE_0 XSCALE_F AREAscale
2001 2002 2003 2004 1 1 0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 3. FUNCTIONS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/200
MAT83 curve
# X Y
0 1
1 1
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/2001
Fct_0N
# X Y
0 .5
1 .5
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/2002
Fct_0S
# X Y
0 .5
1 .5
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/2003
Fct_fN
# X Y
0 1
1 1
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/2004
Fct_fS
# X Y
0 1
1 1
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|Comments
- This law is compatible with 8-noded hexadedron elements (/BRICK) only. It is only compatible with /PROP/TYPE43.
- Stiffness modulus and yield
curve:
- The stiffness modulus and stresses are defined per displacement in order
to be independent from the initial height of the solid element.
For example, =210000 MPa/mm means that the normal stress increases by 210000 MPa for each 1 mm of elongation until the yield stress limit specified by the yield stress curve is reached.
- The stiffness in shear direction is assumed to be equal to the stiffness modulus, (Figure 1).
- The Poisson's ratio is equal to zero.
- After reaching the yield stress (defined in fct_ID11), the material goes into the plastic phase. After reach the maximum
stress RN (in tension)
or RS (in shear), the
stress in material will not increase (Figure 1).
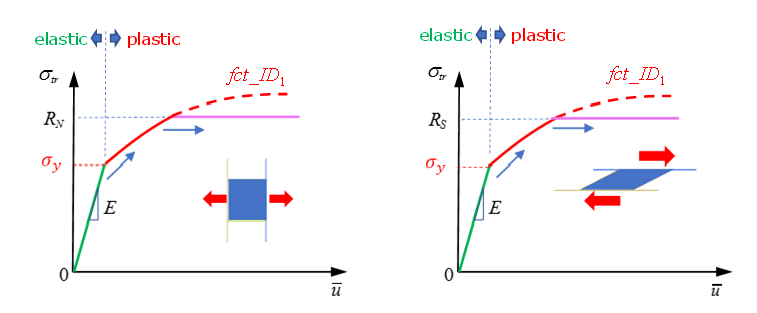
Figure 1. - The plastic displacement is accounted for when fct_ID1 is specified. This is usually a non-decreasing function, which
represents true stress as a function of the plastic displacement. The
first abscissa value of the function should be “0” and the first
ordinate value is the "yield stress". The function may have a stress
decrease portion to model material damage.
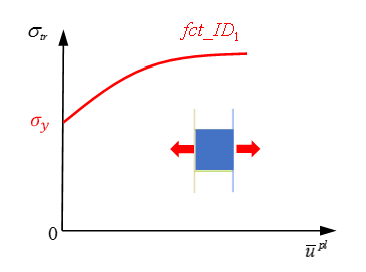
Figure 2.
- The stiffness modulus and stresses are defined per displacement in order
to be independent from the initial height of the solid element.
- Plastic displacement.The complete element displacement can be subdivided into an elastic portion (before yield stress is reached) and a portion of the plastic displacement . In the simplest case of uni-axial tension and compression, plastic displacement is calculated as:
(1) Total normal displacement is the sum of plastic normal displacement and elastic normal displacement.
- The material behavior is identical in tension and compression. The normal and shear DOF are not coupled in the elastic region.
- The normal and shear DOF are
coupled in the plastic region. The normalized effective true stress (
) is calculated from normal (
) and shear stress (
), as:
(2) Where,- and are the functions of fct_IDN and fct_IDS.
- fct_IDN and fct_IDS specify a scaling coefficient for normal and shear stress as a function of the plastic displacement rate.
-
is
. Where, is the angle between the normal of the lower surface and the normal of the upper surface of the solid element.
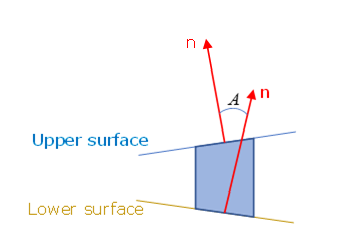
Figure 3. - Parameter is the scale factor used to describe the moment effect (like in the peeling test).
- Parameter
could be fitted with normal and shear
combined test. Like the 60° test or the 30° test. At least one combined test is needed to fit the parameter . Figure 4 shows the effect of on maximum stress in the combined test.
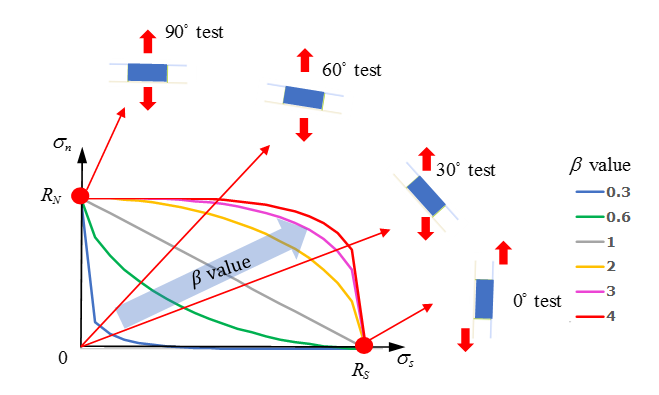
Figure 4.
- The height of the solid element can be equal to zero. The element height does not affect the time step. Only nodal time step is available for this material.
- All nodes of the solid elements must be connected to other shells or solid elements, secondary nodes of rigid body (/RBODY) or secondary nodes of tied interface (/INTER/TYPE2).
- When all nodes of the solid element become free, the element is deleted.
- The rupture criteria for this material is defined by /FAIL/SNCONNECT.
- The true stress will be taken
from fct_ID1 as:
(3) With, being the function of fct_ID1