Spring Type Pretensioners (TYPE32)
Pretensioner expected behavior is as follows: before pretensioning, a piston is fixed in its initial position; when activated, the piston is pushed and cannot slide once the piston has reached the end of its slide, it is unable to slide further in any direction in the opposite direction from its actual position
Pretensioner Model
Linear Model
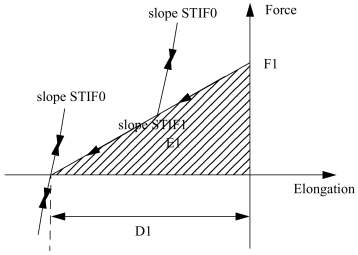
Figure 1.
is also used as unloading stiffness before the end of the piston's slide, and as both loading and unloading stiffness at the end of the piston's slide. should be large enough to allow locking.
Nonlinear Model
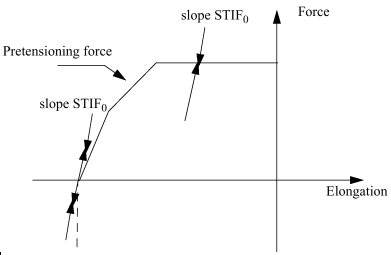
Figure 2.
is spring stiffness before sensor activation. Depending on the input, pretensioning force is defined as , with either , or , with length of the spring at sensor activation time and at sensor activation time.
Similar use of allows piston locking.
Force Computation
Let the pretensioning force for a linear model, and or or for a nonlinear model.
The force into the pretensioner spring is computed as:
if,
and otherwise.