/LOAD/PBLAST

The Air Blast incident pressure is fitted from experimental data, then blast pressure is deduced from surface orientation to the detonation point. You must provide detonation point, detonation time and equivalent TNT mass.

This is a simplified loading method because the arrival time and incident pressure are not adjusted for obstacles. It also does not take into account confinement or ground effects.

Format

Definitions

Comments

1. At a given radius $R$ from explosion center both incident and reflected pressure wave are supposed to follow Friedlander’s equation:(1)
   $${\mathrm{P}}_{Friedlander}\left(t\right)=P_{\max }\cdot e^{\frac{t-t_a}{\text{Δ}{t}_{+}}}\left(1-\frac{t-t_a}{\text{Δ}{t}_{+}}\right)$$
   Where, $P_{\max },\text{Δ}{t}_{+},t_a$ are experimentally known at a given scaled distance $\frac{R}{W^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}$ ( $W$ is explosive mass). If the I_z = 1, then $R$ =constant, but if I_z =2, then $R=R\left(t\right)$ is changing with time.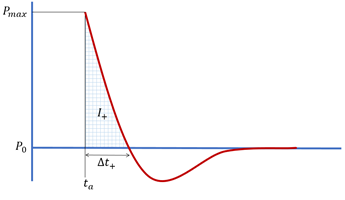

   
   
   Figure 1. Blast Profile from Friedlander Equation

   Radioss proceeds to a fitting to match experimental data. ¹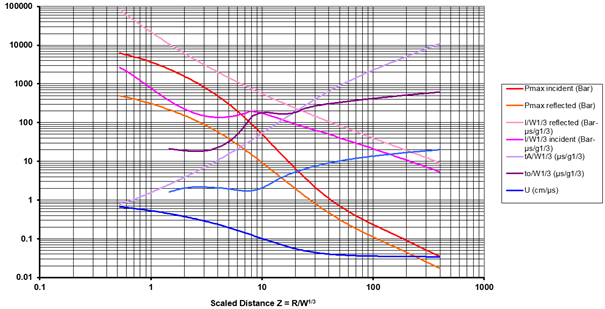

   
   
   Figure 2. Wave Parameter from Spherical TNT Explosion in Free Air at Sea Level

   These fitted time history function ${\mathrm{P}}_{incident}\left(t\right)$ and ${\mathrm{P}}_{reflected}\left(t\right)$ are also used to compute blast loading ${\mathrm{P}}_{BLAST}\left(t\right)$ at a given face centroid Z’ (Figure 3). ²(2)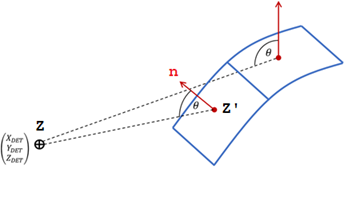

   $${\mathrm{P}}_{BLAST}\left(t\right)=\{\begin{array}{c}{\cos }^2\theta \cdot {\mathrm{P}}_{reflected}\left(t\right)+\left(1+{\cos }^2\theta -2\cos \theta \right)\cdot {\mathrm{P}}_{incident}\left(t\right)\text{ if }\cos \theta >0\\ {\mathrm{P}}_{incident}\left(t\right)\text{ if }\cos \theta \le 0\end{array}$$

   
   
   Figure 3. Blast Pressure Applied on a Face Centroid Z’ . Depends on Face Orientation

   Where,

   $\theta$

   Angle between the surface segment (centroid Z’) and the direction to detonation point

   This means that blast pressure is equal to reflected pressure if segment is directly facing the detonation point, and equal to incident pressure if segment is not facing the detonation point. This modeling is simple because arrival time and incident pressure are not adjusted with shadowing of the related structure. It also does not into account confinement and tunnel effect.

   This also requires the surface to have outward normal vector.

2. If W_TNT is not set, then mass is zero and no pressure will be loaded on the related surface. If modeled explosive is not TNT, then an equivalent TNT mass must be provided.
3. The experimental data uses the unit system {cm, g, µs}. The units defined in /BEGIN will be used to convert the experimental data units to the model units. Therefore, the units defined in /BEGIN must correctly match the units used in the model.
4. It is possible to skip computation time from $T=0$ to $t^{*}=\inf \left(T_{arrival}\right)$ . The shift value is automatically computed during Starter execution. To disable computation up to $t^{*}$ , then I_tShift value must be equal to 2.

   
   
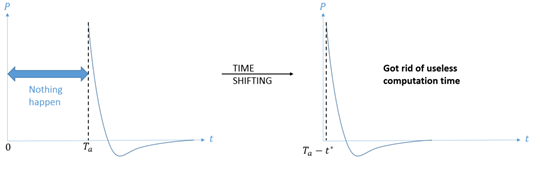
   Figure 4. I_tShift Enables to Skip Computation Time Up to First Wave Arrival Time

5. The $N_{dt}$ parameter can impose a minimal time step if structural one is not large enough. Imposing $\text{Δ}{t}_{blast}=\frac{\inf \left(T_0\right)}{N_{dt}}$ ensures that there are sufficient time steps during positive phase, i.e. during the exponential decrease of the blast wave. By default, $N_{dt}=100$ .

   
   
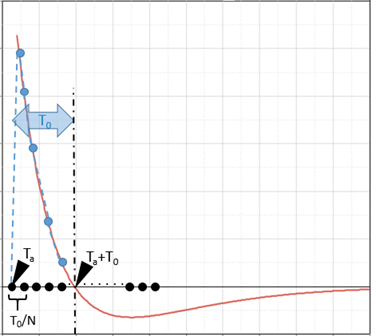
   Figure 5.