Turbulent Wall
Turbulent wall elements define the closure of the system with model diffusive equations.
Turbulent wall conditions are set automatically in elements having at least one node with fixed boundary conditions (111 ... ... ...) or with Lagrangian conditions (... ... ... 111).
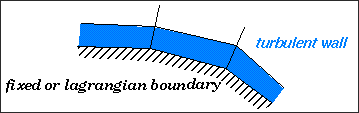
Figure 1.
Neglecting to declare nodal boundary conditions on the wall boundaries of the system can lead to indetermination and to divergence. Using the model implies you must have at least one turbulent wall in your problem.
Wall Element Size
Usually, the value of is considered as critical and for tubes, you get good results for values of as high as 3000. Reasonable values are between 100 and 1000.
- Friction velocity
- Element size perpendicular to wall
- Laminar kinematic velocity
Where, is the turbulent kinematic viscosity.
Generally, meshes are built up with respect to affordability with some kind of trade-off on the value of . If this value is too high, it means that the boundary layer will be poorly integrated. For open cases where the boundary layer often detaches, the mesh size in the wake of the body is mainly governed by the size of eddies. In this case, one can think accuracy is not governed by the wall element size, but by the quality of the algorithm.