/MAT/LAW18 (THERM)

Block Format Keyword This law describes thermal material.

Format

(1) (2) (3) (4) (5) (6) (7) (8) (9) (10)
/MAT/LAW18/mat_ID or /MAT/THERM/mat_ID
mat_title
ρ i ρ 0            
ρ   0 C p A B        
fct_IDT T0 FscaleT          
fct_IDsph fct_IDas Fscalesph FscaleE FscaleK    

Definitions

Field Contents SI Unit Example
mat_ID Material identifier

(Integer, maximum 10 digits)

  
mat_title Material title

(Character, maximum 100 characters)

  
ρ i Initial density

(Real)

 [ kg m 3 ]
ρ 0 Reference density used in E.O.S (equation of state).

Default ρ 0 = ρ i (Real)

 [ kg m 3 ]
ρ   0 C p Specific heat

(Real)

 [ kg s 3 ⋅ m ⋅ K ]
A Conductivity coefficient A

(Real)

 [ W m 2 K ]
B Conductivity coefficient B

(Real)

  
fct_IDT Function f(t) identifier for T. 9
= 0
T is computed
= n
T=T0⋅f(t)

(Integer)

  
T0 Initial temperature

Default = 300K (Real)

 [ K ]
FscaleT Time scale factor

(Real)

  
fct_IDsph Function g(T, E) identifier for temperature vs energy. 7

(Integer)

  
fct_IDas Function h(k, T) identifier for conductivity vs temperature.

(Integer)

  
Fscalesph Temperature scale factor.

(Real)

 [ K ]
FscaleE Energy scale factor.

(Real)

 [ J ]
FscaleK Conductivity scale factor.

(Real)

 [ W m 2 K ]

Comments

  1. This material can be used:
    • as purely thermal material (only Line 4 is read)
    • as boundaries conditions (temperature or flux) (use Line 5)
  2. The k MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi ov2DaebbnrfifHhDYfgasaacH8akY=xipgYlh9vqqj=hEeei0xXdbb a9frFf0=yqFf0dbba91qpepeI8k8fiI+fsY=rqaqpepae9pg0Firpe pesP0xe9Fve9Fve9qapdbaGaaiGadiWaamaaceGaaqaacaqbaaGcba Gaam4Aaaaa@3AC6@ (thermal conductivity) is computed as:(1)
    k = A + B ⋅ T MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4Aaiabg2 da9iaadgeacqGHRaWkcaWGcbGaeyyXICTaamivaaaa@3D7F@
  3. The α (thermal diffusivity) is computed as:(2)
    α = k / ρ 0 C p MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqySdeMaey ypa0Jaam4Aaiaac+cacqaHbpGCdaWgaaWcbaGaaGimaaqabaGccaWG dbWaaSbaaSqaaiaadchaaeqaaaaa@3ED8@

    Where, C p MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4qamaaBa aaleaacaWGWbaabeaaaaa@37E0@ is the heat capacity at constant pressure.

  4. The k MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi ov2DaebbnrfifHhDYfgasaacH8akY=xipgYlh9vqqj=hEeei0xXdbb a9frFf0=yqFf0dbba91qpepeI8k8fiI+fsY=rqaqpepae9pg0Firpe pesP0xe9Fve9Fve9qapdbaGaaiGadiWaamaaceGaaqaacaqbaaGcba Gaam4Aaaaa@3AC6@ (thermal conductivity) is given by curve f c t ​ _ ​ I D a s = k ( T ) MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi ov2DaebbnrfifHhDYfgasaacH8akY=xipgYlh9vqqj=hEeei0xXdbb a9frFf0=yqFf0dbba91qpepeI8k8fiI+fsY=rqaqpepae9pg0Firpe pesP0xe9Fve9Fve9qapdbaGaaiGadiWaamaaceGaaqaacaqbaaGcba GaamOzaiaadogacaWG0bGaaGzaVlaac+facaaMb8Uaamysaiaadsea daWgaaWcbaGaamyyaiaadohaaeqaaOGaeyypa0Jaam4AaiaacIcaca WGubGaaiykaaaa@486C@ .
  5. The α (thermal diffusivity) is computed with curve fct_IDsph α = k / ρ 0 C p with, d E d T = C p .
  6. Function g(T, E) is similar to the following curve:

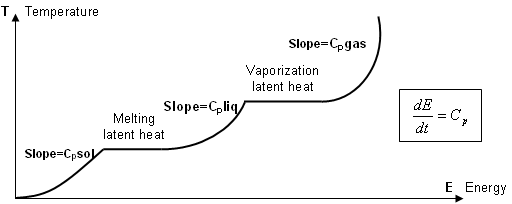
    Image15
    Figure 1.
  7. If fct_IDsph ≠ 0,(3)
    E s p e c i f i c = E int ρ 0 F s c a l e E MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi ov2DaebbnrfifHhDYfgasaacH8akY=xipgYlh9vqqj=hEeei0xXdbb a9frFf0=yqFf0dbba91qpepeI8k8fiI+fsY=rqaqpepae9pg0Firpe pesP0xe9Fve9Fve9qapdbaGaaiGadiWaamaaceGaaqaacaqbaaGcba GaamyramaaBaaaleaacaWGZbGaamiCaiaadwgacaWGJbGaamyAaiaa dAgacaWGPbGaam4yaaqabaGccqGH9aqpdaWcaaqaamaaliaabaGaam yramaaBaaaleaaciGGPbGaaiOBaiaacshaaeqaaaGcbaGaeqyWdi3a aSbaaSqaaiaaicdaaeqaaaaaaOqaaiaadAeacaWGZbGaam4yaiaadg gacaWGSbGaamyzamaaBaaaleaacaWGfbaabeaaaaaaaa@5057@

    T = f s p h ( E s p e c i f i c ) ⋅ F s c a l e s p h MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi ov2DaebbnrfifHhDYfgasaacH8akY=xipgYlh9vqqj=hEeei0xXdbb a9frFf0=yqFf0dbba91qpepeI8k8fiI+fsY=rqaqpepae9pg0Firpe pesP0xe9Fve9Fve9qapdbaGaaiGadiWaamaaceGaaqaacaqbaaGcba Gaamivaiabg2da9iGacAgadaWgaaWcbaGaam4CaiaadchacaWGObaa beaakiaacIcacaWGfbWaaSbaaSqaaiaadohacaWGWbGaamyzaiaado gacaWGPbGaamOzaiaadMgacaWGJbaabeaakiaacMcacqGHflY1caGG gbGaai4CaiaacogacaGGHbGaaiiBaiaacwgadaWgaaWcbaGaam4Cai aadchacaWGObaabeaaaaa@542E@

    Where, f s p h MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi ov2DaebbnrfifHhDYfgasaacH8akY=xipgYlh9vqqj=hEeei0xXdbb a9frFf0=yqFf0dbba91qpepeI8k8fiI+fsY=rqaqpepae9pg0Firpe pesP0xe9Fve9Fve9qapdbaGaaiGadiWaamaaceGaaqaacaqbaaGcba GaciOzamaaBaaaleaacaWGZbGaamiCaiaadIgaaeqaaaaa@3DC8@ is the function of fct_IDsph.

  8. If fct_IDsph = 0,(4)
    T = E int ⁡ sph

    with S p h = ρ 0 C p = S p e c i f i c H e a t MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiaadc hacaWGObGaeyypa0JaeqyWdi3aaSbaaSqaaiaaicdaaeqaaOGaam4q amaaBaaaleaacaWGWbaabeaakiabg2da9iaadofacaWGWbGaamyzai aadogacaWGPbGaamOzaiaadMgacaWGJbGaamisaiaadwgacaWGHbGa amiDaaaa@4A44@

  9. If fct_IDT ≠ 0,(5)
    T = f ( T i m e ) ⋅ T 0 MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=HhbHc9v8 qqaqFr0xb9pg0xb9qqaqFn0dXdHiVcFbIOFHK8Feea0dXdar=Jb9hs 0dXdHuk9fr=xfr=xfrpeWZqaaiaaciWacmaadaGabiaaeaGaauaaaO qaaiaadsfacqGH9aqpciGGMbGaciikaiaadsfacaWGPbGaamyBaiaa dwgacaGGPaGaeyyXICTaamivamaaBaaaleaacaaIWaaabeaaaaa@4622@

    with T i m e = T i m e ⋅ F s c a l e T MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=HhbHc9v8 qqaqFr0xb9pg0xb9qqaqFn0dXdHiVcFbIOFHK8Feea0dXdar=Jb9hs 0dXdHuk9fr=xfr=xfrpeWZqaaiaaciWacmaadaGabiaaeaGaauaaaO qaaiaadsfacaWGPbGaamyBaiaadwgacqGH9aqpcaWGubGaamyAaiaa d2gacaWGLbGaeyyXICTaamOraiaadohacaWGJbGaamyyaiaadYgaca WGLbWaaSbaaSqaaiaadsfaaeqaaaaa@4B57@ ; E int = T ⋅ s p h MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqOqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGfbWaaS baaSqaaiGacMgacaGGUbGaaiiDaaqabaGccqGH9aqpcaWGubGaeyyX ICTaam4CaiaadchacaWGObaaaa@424B@ .

  10. If fct_IDas ≠ 0,
    (6)
    T = T F s c a l e s p h MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi ov2DaebbnrfifHhDYfgasaacH8akY=xipgYlh9vqqj=hEeei0xXdbb a9frFf0=yqFf0dbba91qpepeI8k8fiI+fsY=rqaqpepae9pg0Firpe pesP0xe9Fve9Fve9qapdbaGaaiGadiWaamaaceGaaqaacaqbaaGcba Gaamivaiabg2da9maalaaabaGaamivaaqaaiaadAeacaWGZbGaam4y aiaadggacaWGSbGaamyzamaaBaaaleaacaWGZbGaamiCaiaadIgaae qaaaaaaaa@4510@

    A = f a s ( T ) ⋅ F s c a l e E MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbc9v8 qqaqFr0xb9pg0xb9qqaqFn0dXdHiVcFbIOFHK8Feea0dXdar=Jb9hs 0dXdHuk9fr=xfr=xfrpeWZqaaiaaciWacmaadaGabiaaeaGaauaaaO qaaiaadgeacqGH9aqpciGGMbWaaSbaaSqaaiaadggacaWGZbaabeaa kmaabmaabaGaamivaaGaayjkaiaawMcaaiabgwSixlaadAeacaWGZb Gaam4yaiaadggacaWGSbGaamyzamaaBaaaleaacaWGfbaabeaaaaa@4A22@ ; B = 0 MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOqaiabg2 da9iaaicdaaaa@387E@

    Where, f a s MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbc9v8 qqaqFr0xb9pg0xb9qqaqFn0dXdHiVcFbIOFHK8Feea0dXdar=Jb9hs 0dXdHuk9fr=xfr=xfrpeWZqaaiaaciWacmaadaGabiaaeaGaauaaaO qaaiGacAgadaWgaaWcbaGaamyyaiaadohaaeqaaaaa@3D3E@ is the function of fct_IDas.