/GJOINT

Block Format Keyword Defines complex (gear-type) joints. This keyword is not available for SPMD computation.

Format

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
/GJOINT/`type`/`joint_ID`/`unit_ID`
`joint_title`
`node_ID`₀	`Fscale`_V		`Mass`		`Inertia`		`node_ID`₁	`node_ID`₂	`node_ID`₃
`Mass`₁		`Inertia`₁		`r`_1x		`r`_1y		`r`_1z
`Mass`₂		`Inertia`₂		`r`_2x		`r`_2y		`r`_2z
`Mass`₃		`Inertia`₃		`r`_3x		`r`_3y		`r`_3z

Definitions

Field	Contents	SI Unit Example
`type`	Input type (see table below for available keywords)
`joint_ID`	Gear type joint identifier (Integer, maximum 10 digits)
`unit_ID`	Unit Identifier (Integer, maximum 10 digits)
`joint_title`	Gear type joint title (Character, maximum 100 characters)
`node_ID`₀	Primary node identifier (position node) (Integer)
`Fscale`_V	Velocity scale factor Default = 1.0 (Real)	$[\frac{m}{s}]$
`Mass`	Added mass to primary node Default = 0.0 (Real)	$[kg]$
`Inertia`	Added to primary node inertia Default = 0.0 (Real)	$[kg \cdot m^{2}]$
`node_ID`₁	Node identifier `N`₁ (Integer)
`node_ID`₂	Node identifier `N`₂ (Integer)
`node_ID`₃	Node identifier `N`₃ - only necessary for differential gear joint. (Integer)
`Mass`₁	Added mass to `node_ID`₁ Default = 0.0 (Real)	$[kg]$
`Inertia`₁	Added to `node_ID`₁ inertia Default = 0.0 (Real)	$[kg \cdot m^{2}]$ ]
`r`_1x	Local axis X component Default = 1.0 (Real)
`r`_1y	Local axis Y component Default = 0.0 (Real)
`r`_1z	Local axis Z component Default = 0.0 (Real)
`Mass`₂	Added mass to `node_ID`₂ Default = 0.0 (Real)	$[kg]$
`Inertia`	Added to `node_ID`₂ inertia Default = 0.0 (Real)	$[kg \cdot m^{2}]$ ]
`r`_2x	Local axis X component Default = 1.0 (Real)
`r`_2y	Local axis Y component Default = 0.0 (Real)
`r`_2z	Local axis Z component Default = 0.0 (Real)
`Mass`₃	Added mass to `node_ID`₃ Default = 0.0 (Real)	$[kg]$
`Inertia`₃	Added to `node_ID`₃ inertia Default = 0.0 (Real)	$[kg \cdot m^{2}]$ ]
`r`_3x	Local axis X component Default = 1.0 (Real)
`r`_3y	Local axis Y component Default = 0.0 (Real)
`r`_3z	Local axis Z component Default = 0.0 (Real)

Complex Joint Types

Type: Description
GEAR: ∞ rotational gear
DIFF: ∞ differential gear
RACK: ∞ rack and pinion

Comments

Complex (gear-type) joints belong to the family of kinematic constraints treated by a Lagrange multipliers' method. A joint position is defined by a central node_ID₀, which are connected to two or three secondary nodes. Mass and inertia must be added to all nodes. It is advisable to place the primary node in the mass center of the joint. Kinematic constraints impose relations between secondary nodes velocities.

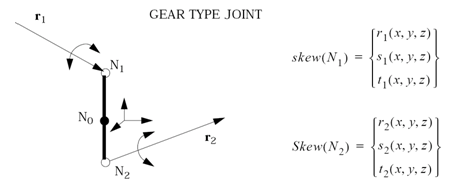
Figure 1.
Translational velocities of gear joint nodes are constrained by a rigid link relation. For the rotational DOF, a scale factor is imposed between velocities of node_ID₁ and node_ID₂, measured in their local coordinates. The corresponding constraint equations are:(1)
$α (Δ ω_{1} \cdot r_{1}) + (Δ ω_{2} \cdot r_{2}) = 0$
(2)
$(Δ ω_{1} \cdot s_{1}) = 0$
(3)
$(Δ ω_{1} \cdot t_{1}) = 0$
(4)
$(Δ ω_{2} \cdot s_{2}) = 0$
(5)
$(Δ ω_{2} \cdot t_{2}) = 0$

Where, $Δ ω_{1} = ω_{1} - ω_{0}$ and $Δ ω_{2} = ω_{2} - ω_{0}$ are relative rotational velocities of node_ID₁ and node_ID₂ with respect to the rigid body rotational velocity.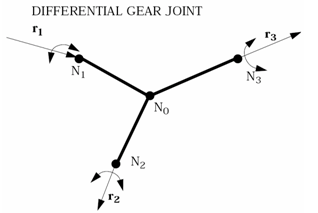

Figure 2.
The rotational velocities of a differential gear joint are constrained by the relations:(6)
$α (Δ ω_{1} \cdot r_{1}) + (Δ ω_{2} \cdot r_{2}) + (Δ ω_{3} \cdot r_{3}) = 0$
(7)
$α (Δ ω_{1} \cdot s_{1}) + (Δ ω_{2} \cdot s_{2}) + (Δ ω_{3} \cdot s_{3}) = 0$
(8)
$α (Δ ω_{1} \cdot t_{1}) + (Δ ω_{2} \cdot t_{2}) + (Δ ω_{3} \cdot t_{3}) = 0$

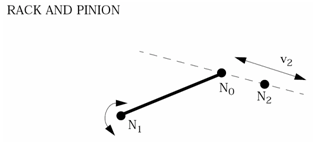
Figure 3.
The rack and pinion joint allows the rotational velocity of node_ID₁ to be transformed to a translational velocity of node_ID₂. The constraint equations for these velocities are:(9)
$α (Δ ω_{1} \cdot r_{1}) + (Δ V_{2} \cdot r_{2}) = 0$
(10)
$α (Δ ω_{1} \cdot s_{1}) + (Δ V_{2} \cdot s_{2}) = 0$
(11)
$α (Δ ω_{1} \cdot t_{1}) + (Δ V_{2} \cdot t_{2}) = 0$
The node_ID₃ is only necessary for a differential gear joint.
This option is not available, if it is applied on:
- a node with a null mass
- a node with a null inertia (except in case of node_ID₂ of a rack type GJOINT)