Reference: Deformable Surface
Model ElementReference_DeformSurface element specifies a deformable surface that is made to pass through the origins of a specified set of markers, using CUBIC spline interpolation.
Description
These markers may be on separate bodies or on a flexible body. As the markers move in space, the surface is recalculated using CUBIC spline interpolation thereby allowing the surface to deform. The surface can be open or closed.
Format
<Reference_DeformSurface
id = "integer"
[ label = "string" ]
u_span = "real"
v_span = "real"
[ end_type = "{NATURAL | PARABOLIC | PERIODIC | CANTILEVER}" ]
[ is_u_closed = "boolean" ]
[ is_v_closed = "boolean" ]
num_marker_row = "integer"
num_marker_col = "integer">
integer integer … integer
… … … …
integer integer … integer
</Reference_DeformSurface>Attributes
- id
- Specifies the element identification number, (integer>0). This number should be unique among all Reference_DeformSurface elements.
- label
- An optional character string that defines a name for the modeling element.
- u_span
- Real value that defines the span of the u parameter. The u parameter goes from -u_span/2 to u_span/2. u_span > 0.
- v_span
- Real value that defines the span of the v parameter. The v parameter goes from -v_span/2 to v_span/2. v_span > 0.
- end_type
-
Select one from NATURAL, PARABOLIC or PERIODIC. 8
Default = NATURAL
- is_u_closed
-
A Boolean value (TRUE or FALSE) that determines whether the markers that define the surface are closed in u or not. 3 4
Default = "FALSE"
- is_v_closed
-
A Boolean value (TRUE or FALSE) that determines whether the markers that define the surface are closed in v or not. 3 5
Default = "FALSE"
- num_marker_row
- Number of markers that define the u curves. 7
- num_marker_col
- Number of markers that define the v curves. 7
Example 1
The figure below demonstrates the use of the Constraint_PTDSF element, along with the Reference_DeformSurface and Post_Graphic elements.
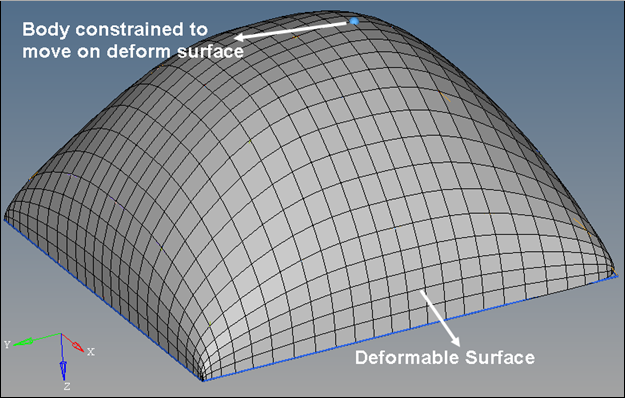
Figure 1. A Body Constrained to Move on a Deformable Surface
<Reference_DeformSurface
id = "1"
end_type = "NATURAL"
num_marker_row = "7"
num_marker_col = "7">
30101490 30101500 30101510 30101520 30101530 30101540 30101540
30101420 30109781 30113791 30117801 30121811 30125821 30101480
30101350 30108711 30112721 30116731 30120741 30124751 30101410
30101120 30102061 30103071 30104081 30105091 30106101 30101130
30101140 30110571 30114581 30118591 30122601 30126611 30101200
30101210 30111641 30115651 30119661 30123671 30127681 30101270
30101280 30101290 30101300 30101310 30101320 30101330 30101340
</Reference_DeformSurface>
<Constraint_PTdSF
id = "1"
i_marker_id = "30107780"
ref_surface_id = "1"
/>
<Post_Graphic
id = "500000"
type = "DeformSurface"
surface_id = "1"
nseg_u = "30"
nseg_v = "30"
/>Example 2
The figures below demonstrate how to define a closed surface. In the images, the direction of U, V is shown and the deformable surface is labeled as S.
a) Closed in u:
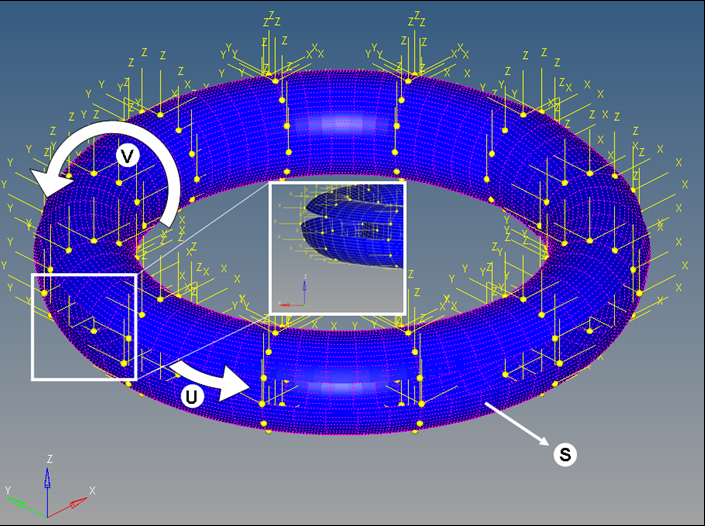
Figure 2. A Deformable Surface Closed in U Space, but not in V
<Reference_DeformSurface
id = "301001"
label = "DeformableSurface 0"
end_type = "NATURAL"
u_span = "1."
v_span = "1."
is_u_closed = "TRUE"
is_v_closed = "FALSE"
num_marker_row = "13"
num_marker_col = "12">
70000000 30102970 30102740 30102500 30102260 30102140 30102020 30102380 70000002 30102620 30102860 70000003
70000005 30102980 30102750 30102510 30102270 30102150 30102030 30102390 70000006 30102630 30102870 70000007
70000009 30102990 30102760 30102520 30102280 30102160 30102040 30102400 70000010 30102640 30102880 70000011
70000013 70000014 30102770 30102530 30102290 30102170 30102050 30102410 70000015 30102650 30102890 70000016
70000018 70000019 30102780 30102540 30102300 30102180 30102060 30102420 70000020 30102660 30102900 70000021
70000023 70000024 30102790 30102550 30102310 30102190 30102070 30102430 70000025 30102670 30102910 70000026
70000028 70000029 30102800 30102560 30102320 30102200 30102080 30102440 70000030 30102680 30102920 70000031
70000033 70000034 30102810 30102570 30102330 30102210 30102090 30102450 70000035 30102690 70000036 70000037
70000039 70000040 30102820 30102580 30102340 30102220 30102110 30102460 70000041 30102700 30102930 70000042
70000044 70000045 30102830 30102590 30102350 30102230 30102100 30102470 70000046 30102710 30102940 70000047
70000049 70000050 30102840 30102600 30102360 30102240 30102120 30102480 70000051 30102720 30102950 70000052
70000054 70000055 30102850 30102610 30102370 30102250 30102130 30102490 70000056 30102730 30102960 70000057
70000000 30102970 30102740 30102500 30102260 30102140 30102020 30102380 70000002 30102620 30102860 70000003
</Reference_DeformSurface>b) Closed in v:
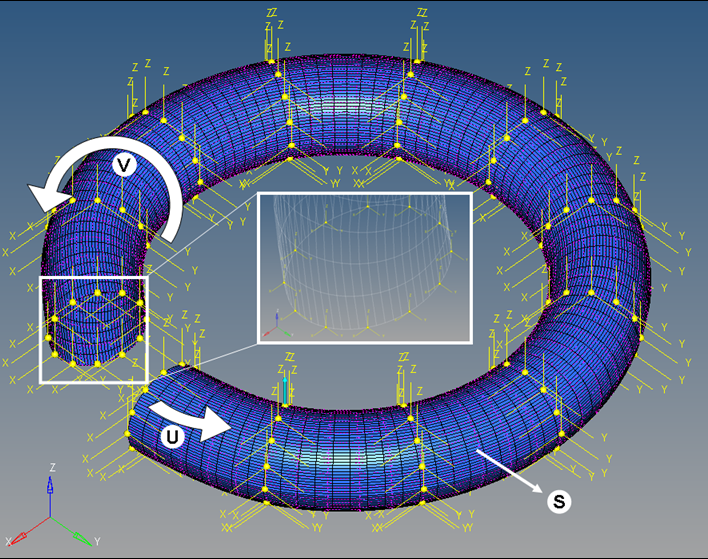
Figure 3. A Deformable Surface Closed in V Space, but not in U
<Reference_DeformSurface
id = "301001"
label = "DeformableSurface 0"
end_type = "NATURAL"
u_span = "1."
v_span = "1."
is_u_closed = "FALSE"
is_v_closed = "TRUE"
num_marker_row = "12"
num_marker_col = "13">
70000000 30102970 30102740 30102500 30102260 30102140 30102020 30102380 70000002 30102620 30102860 70000003 70000000
70000005 30102980 30102750 30102510 30102270 30102150 30102030 30102390 70000006 30102630 30102870 70000007 70000005
70000009 30102990 30102760 30102520 30102280 30102160 30102040 30102400 70000010 30102640 30102880 70000011 70000009
70000013 70000014 30102770 30102530 30102290 30102170 30102050 30102410 70000015 30102650 30102890 70000016 70000013
70000018 70000019 30102780 30102540 30102300 30102180 30102060 30102420 70000020 30102660 30102900 70000021 70000018
70000023 70000024 30102790 30102550 30102310 30102190 30102070 30102430 70000025 30102670 30102910 70000026 70000023
70000028 70000029 30102800 30102560 30102320 30102200 30102080 30102440 70000030 30102680 30102920 70000031 70000028
70000033 70000034 30102810 30102570 30102330 30102210 30102090 30102450 70000035 30102690 70000036 70000037 70000033
70000039 70000040 30102820 30102580 30102340 30102220 30102110 30102460 70000041 30102700 30102930 70000042 70000039
70000044 70000045 30102830 30102590 30102350 30102230 30102100 30102470 70000046 30102710 30102940 70000047 70000044
70000049 70000050 30102840 30102600 30102360 30102240 30102120 30102480 70000051 30102720 30102950 70000052 70000049
70000054 70000055 30102850 30102610 30102370 30102250 30102130 30102490 70000056 30102730 30102960 70000057 70000054
</Reference_DeformSurface>c) Closed in both u and v:
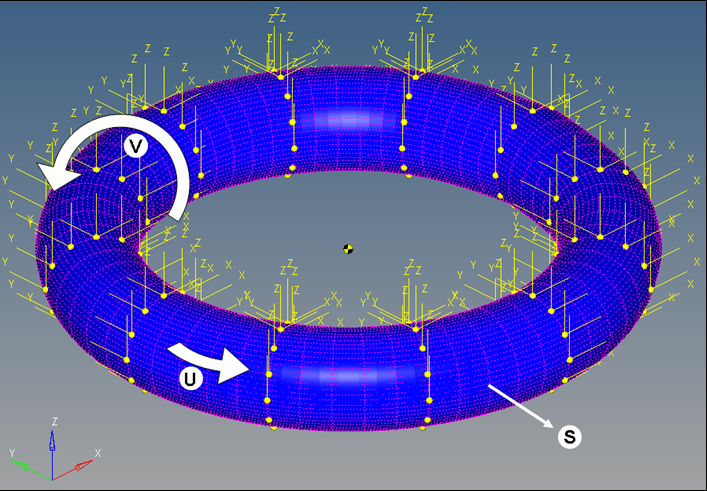
Figure 4. A Deformable Surface Closed in U and V Space
<Reference_DeformSurface
id = "301001"
label = "DeformableSurface 0"
end_type = "NATURAL"
u_span = "1."
v_span = "1."
is_u_closed = "TRUE"
is_v_closed = "TRUE"
num_marker_row = "13"
num_marker_col = "13">
70000000 30102970 30102740 30102500 30102260 30102140 30102020 30102380 70000002 30102620 30102860 70000003 70000000
70000005 30102980 30102750 30102510 30102270 30102150 30102030 30102390 70000006 30102630 30102870 70000007 70000005
70000009 30102990 30102760 30102520 30102280 30102160 30102040 30102400 70000010 30102640 30102880 70000011 70000009
70000013 70000014 30102770 30102530 30102290 30102170 30102050 30102410 70000015 30102650 30102890 70000016 70000013
70000018 70000019 30102780 30102540 30102300 30102180 30102060 30102420 70000020 30102660 30102900 70000021 70000018
70000023 70000024 30102790 30102550 30102310 30102190 30102070 30102430 70000025 30102670 30102910 70000026 70000023
70000028 70000029 30102800 30102560 30102320 30102200 30102080 30102440 70000030 30102680 30102920 70000031 70000028
70000033 70000034 30102810 30102570 30102330 30102210 30102090 30102450 70000035 30102690 70000036 70000037 70000033
70000039 70000040 30102820 30102580 30102340 30102220 30102110 30102460 70000041 30102700 30102930 70000042 70000039
70000044 70000045 30102830 30102590 30102350 30102230 30102100 30102470 70000046 30102710 30102940 70000047 70000044
70000049 70000050 30102840 30102600 30102360 30102240 30102120 30102480 70000051 30102720 30102950 70000052 70000049
70000054 70000055 30102850 30102610 30102370 30102250 30102130 30102490 70000056 30102730 30102960 70000057 70000054
70000000 30102970 30102740 30102500 30102260 30102140 30102020 30102380 70000002 30102620 30102860 70000003 70000000
</Reference_DeformSurface>Comments
- Reference_DeformSurface is quite
similar to Reference_ParamSurface, except it can deform.
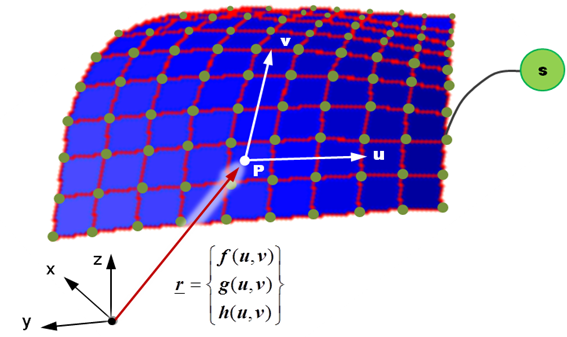
Figure 5. The Definition of a Reference_DeformSurfaceReferring to the figure above, the shape of the surface S is defined by the cubic spline that passes through the instantaneous origins of a set of markers. The origins are shown as green spheres in the image above. Reference_DeformSurface is therefore a parametric, deformable surface in 3D space. u and v are free surface parameters that define the extent of the surface.
- u can vary from umin = - u_span/2 to umax = + u_span/2
- v can vary from vmin = - v_span/2 to vmax = + v_span/2
The coordinates of any arbitrary P point on the surface, as measured in OXYZ, can be represented uniquely in terms of the free parameters u, v, with three cubic-spline functions f(u,v), g(u,v) and h(u,v) that define the x-, y- and z-coordinates of P.
- The markers used to define the u and v curves are
arranged as follows:
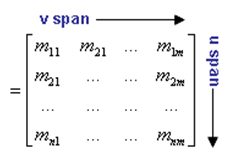
Figure 6. Marker Matrixsuch that the total number of markers for (u x v) = (n x m).
- Reference_DeformCurve can be opened
or closed in either the u or v domains.
- A surface closed in u has the property:
- { x(umin,v) y(umin,v) z(umin,v) } = { x(umax,v) y(umax,v) z(umax,v) }
- A surface closed in v has the property:
- { x(u,vmin) y(u,vmin) z(u,vmin) } = { x(u,vmax) y(u,vmax) z(u,vmax) }
- A surface closed in u and v has the properties:
- { x(umin,v) y(umin,v) z(umin,v) } = { x(umax,v) y(umax,v) z(umax,v) }, and,
- { x(u,vmin) y(u,vmin) z(u,vmin) } = { x(u,vmax) y(u,vmax) z(u,vmax) }
- A surface closed in u has the property:
- To define the surface as closed in the u space, you must
do the following:
- Set is_u_closed = "TRUE"
- Ensure that the first and last markers in every column are the same.
- See Example 2a for reference.
- To define the surface as closed in the v space, you must
do the following:
- Set is_v_closed = "TRUE"
- Ensure that the first and last markers in every row are the same.
- See Example 2b for reference.
- To define the surface as closed in both the u and v
space, you must do the following:
- Set is_u_closed = "TRUE"
- Set is_v_closed = "TRUE"
- Ensure that the first and last markers in every column are the same.
- Ensure that the first and last markers in every row are the same.
- See Example 2c for reference.
- The minimum number of markers required to define a
surface is listed below:

Figure 7. - Reference_DeformSurface uses a CUBIC
spline interpolation that requires assumptions on the second derivative of the
interpolating function at the ends of the surface. The keywords NATURAL,
PARABOLIC, and PERIODIC represent the three standard assumptions defined as
follows:
- NATURAL (or free):
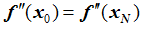
- PARABOLIC:
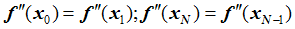
- PERIODIC:
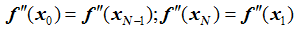
- NATURAL (or free):
- The Reference_DeformSurface element does not possess any inherent inertia, stiffness or damping properties.
- A deformable surface is used in the definition of a Constraint_PTdSF, which constrains a point on a body to slide along the deformable surface.
- This deformable surface is also used in the definition of a Force_PTdSF, which prevents a point on a body from penetrating into the deformable surface, but allows lift-off and sliding.
- If the Reference_DeformSurface is used for a Force_PTdSF element, then the surface normal is required. The surface normal is calculated at a point on the surface as the cross product between the tangent to the u curve and the tangent to the v curve at that point. The attribute flip_normal can be used to flip the direction of the normal vector. See the Force_PTdSF element for more details.
- Occasionally, for an open deformable surface (open in
U, open in V or open in both U and V), you will see the message,
"Parameter U='value' goes out of intended range". This
condition occurs because the numerical methods have no obvious way to enforce
the limit: - u_span/2 ≤ u ≤ + u_span/2 and -
v_span/2 ≤ v ≤ + v_span/2. In such a
situation, MotionSolve holds the "U" or "V" value at
the boundary (-u_span/2 or +u_span/2 for u
and -v_span/2 or +v_span/2 for v) and
continues with the simulation until the point falls back in range. If the model
is well-defined, the point will fall back in range. Note: If you see such a message in your simulation, please check the results carefully as they may be wrong, even though the simulation completes successfully.