Laminar Flow Through a Channel with Heated Walls
In this application, AcuSolve is used to simulate high Peclet number laminar flow through a channel with heated walls. AcuSolve results are compared with analytical results adapted from Hua and Pillai (2010). The close agreement of AcuSolve results with analytical results validates the ability of AcuSolve to model cases involving heat transfer to a moving fluid with a high Peclet number.
Problem Description
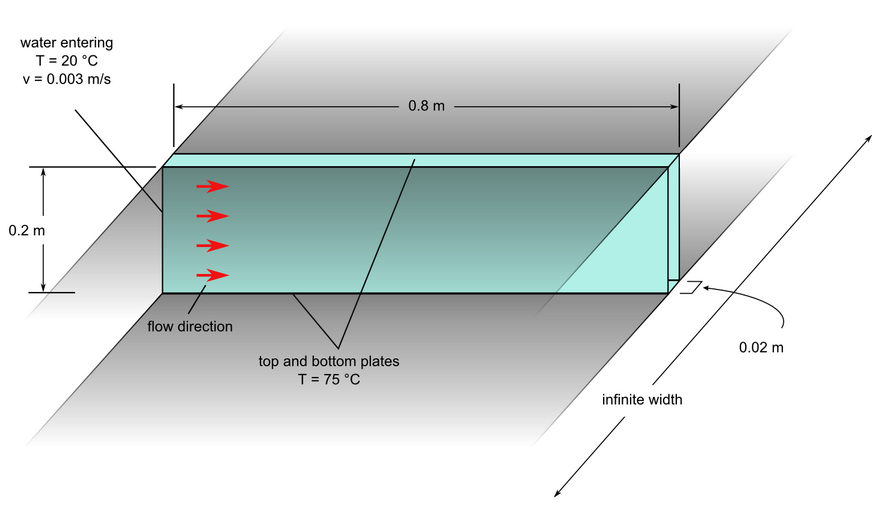
Figure 1. Critical Dimensions and Parameters for Simulating Laminar Flow Through a Channel with Heated Walls
Figure 2. Mesh (Top Half of the Channel) used for Simulating Laminar Flow Through a Channel with Heated Walls
AcuSolve Results
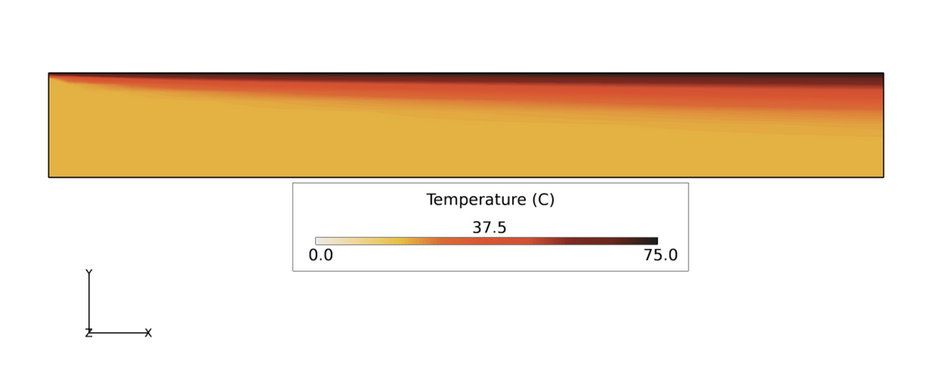
Figure 3. Temperature Contours Along the Top Half of a Heated Channel
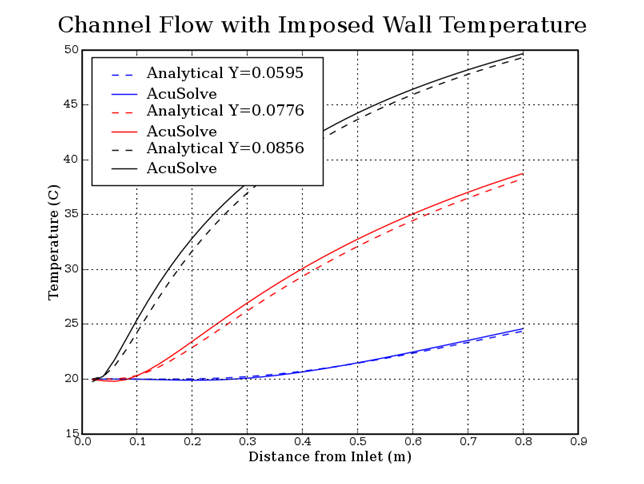
Figure 4. Temperature Plotted Against Distance from Inlet for 3 Different Heights from the Channel Center Line
Summary
The AcuSolve results compare well with the analytical results for the development of a thermal boundary layer in a heated channel. In this application, the model is set up to yield large gradients as the flow convects away from the inlet. The boundary conditions and mesh size were chosen specifically to yield a high Peclet number. The element Peclet number in the flow direction in this case is Pe=30.0, as calculated from the following equation.
where is the density, the heat capacity, ν the velocity, the length, and k the thermal conductivity.
This example shows the robustness of the stabilized technique in AcuSolve when element Peclet number is high. Note that standard Galerkin finite element formulations become unstable when the element Peclet number is greater than 1.0.
Simulation Settings for Laminar Flow Through a Channel with Heated Walls
AcuConsole database file: <your working directory>\channel_laminar_heat\channel_laminar_heat.acs
Global
- Problem Description
- Analysis type - Steady State
- Temperature equation - Advective Diffusive
- Turbulence equation - Laminar
- Auto Solution Strategy
- Relaxation factor - 0.4
- Material Model
- Fluid_Material
- Density - 1000.0 kg/m3
- Specific Heat - 1000 J/kg-K
- Viscosity - 1.0e-12 kg/m-sec
- Conductivitiy - 1.0 W/m-K
Model
- Fluid_Material
- Volumes
- Fluid
- Element Set
- Material model - Fluid_Material
- Element Set
- Fluid
- Surfaces
- Inlet
- Simple Boundary Condition
- Type - Inflow
- Inflow type - Velocity
- X velocity - 0.003 m/sec
- Temperature - 20 °C
- Simple Boundary Condition
- Outlet
- Simple Boundary Condition
- Type - Outflow
- Simple Boundary Condition
- Symm_MaxZ
- Simple Boundary Condition
- Type - Slip
- Simple Boundary Condition
- Symm_MinY
- Simple Boundary Condition
- Type - Slip
- Simple Boundary Condition
- Symm_MinZ
- Simple Boundary Condition
- Type - Slip
- Simple Boundary Condition
- Wall
- Simple Boundary Condition
- Type - Wall
- Temperature BC type - Value
- Temperature - 75 °C
- Simple Boundary Condition
- Inlet
References
Hua Tan and K. M. Pillai. "Numerical Simulation of Reactive Flow in Liquid Composite Molding Using Flux-Corrected Transport (FCT) Based Finite Element/Control Volume (FE/CV) Method". International Journal of Heat and Mass Transfer. 53:2256-2271, 2010.