/INTER/TYPE25
Block Format Keyword TYPE25 is a general nodes to surface contact interface using the penalty method. The penalty stiffness is constant and therefore the time step is not affected.
Solid elements have zero contact gap thickness. Contact inputs can be defined as a single surface, surface to surface, or nodes to surface.
This contact interface can replace interface TYPE3, TYPE5, TYPE7, TYPE19 or TYPE24.
This interface is not available with the implicit solution.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /INTER/TYPE25/inter_ID/unit_ID | |||||||||
| inter_title | |||||||||
| surf_ID1 | surf_ID2 | Istf | Ithe | Igap | Irem_i2 | Idel | Iedge | ||
| grnd_IDs | Gap_scale | %mesh_size | Gap_max_s | Gap_max_m | |||||
| Stmin | Stmax | Igap0 | Ishape | Edge_angle | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| Stfac | Fric | Tstart | Tstop | ||||||
| IBC | IVIS2 | Inacti | VISs | ||||||
| Ifric | Ifiltr | Xfreq | sens_ID | fric_ID | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| C6 | |||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| ViscFluid | SigMaxAdh | ViscAdhFact | |||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| Kthe | fct_IDK | Tint | Ithe_form | AscaleK | |||||
| Frad | Drad | Fheats | Fheatm | fct_IDF | |||||
| fct_IDc | Dcond | ||||||||
Definitions
| Field | Contents | SI Unit Example |
|---|---|---|
| inter_ID | Interface
identifier. (Integer, maximum 10 digits) |
|
| unit_ID | Unit Identifier. (Integer, maximum 10 digits) |
|
| inter_title | Interface
title. (Character, maximum 100 characters) |
|
| surf_ID1 | First surface identifier. 1 (Integer) |
|
| surf_ID2 | Second surface
identifier. (Integer) |
|
| Istf | Interface stiffness
definition flag. 2
(Integer) |
|
| Ithe | Heat transfer flag.
Thermal exchange is not available for edge to edge. (Integer) |
|
| Igap | Gap/element option flag.
3
|
|
| Irem_i2 | Deactivating flag for the
secondary node, if the same contact pair (nodes) has been defined in
interface TYPE2.
|
|
| Idel | Node and segment deletion flag.
|
|
| Iedge | Edge contact options.
Contact occurs between main and secondary edges which are
automatically extracted from surf_ID1 and surf_ID2. Sharp edges for external solid faces are defined using the angle
Edge_angle.
(Integer) |
|
| grnd_IDs | Nodes group
identifier. 1 If defined, node group will be added as secondary nodes. (Integer) |
|
| Gap_scale | Gap scale factor for all
Igap options. Default = 1.0 (Real) |
|
| %mesh_size | Percentage of mesh size
(used only when Igap = 3). Default = 0.4 (Real) |
|
| Gap_max_s | Secondary maximum gaps.
3 Default = 1030 (Real) |
|
| Gap_max_m | Main maximum gaps. 3 Default = 1030 (Real) |
|
| Stmin | Minimum stiffness (used
only when Istf >
1 and Istf < 7). 2 (Real) |
|
| Stmax | Maximum stiffness (used
only when Istf > 1
and Istf < 7). 2 Default = 1030 (Real) |
|
| Igap0 | Gap modification flag for
secondary shell nodes on the free edges or shell elements. 3
(Integer) |
|
| Ishape | Flag defining the shape of
the gap along the surface(s) external border in the node to surface contact.
(Integer) |
|
| Edge_angle | Edge angle Only used with Iedge =11,13. Sharp edges are included in edge contact, if the angle between two segments which share the same edge is smaller than Edge_angle value. Default = 135° (Real) |
|
| Stfac | Interface stiffness scale
factor. 2 Default = 1.0 (Real) |
|
| Fric | Coulomb friction (if fct_IDF= 0). Coulomb friction scale factor (if fct_IDF≠ 0). Default = 0.0 (Real) |
|
| Tstart | Start time. 10
(Real) |
|
| Tstop | Temporary deactivation
time. 10 Default = 1030 (Real) |
|
| IBC | Deactivation flag of
boundary conditions at impact. (Boolean) |
|
| Inacti | Initial penetration flag.
(Integer) |
|
| VISs | Critical damping
coefficient on interface stiffness. Default = 0.05 (Real) |
|
| Ifric | Friction formulation
flag. Only used if fric_ID is not defined.
For edge to edge contact, only static Coulomb friction law is available. (Integer) |
|
| Ifiltr | Friction filtering flag.
(Integer) |
|
| Xfreq | Filtering
coefficient. Default = 1.0 (Real) |
|
| sens_ID | Sensor identifier to
activate/deactivate the interface. (Integer) |
|
| fric_ID | Friction identifier for
friction definition for selected pairs of parts.
For edge to edge contact, only isotropic friction is considered. If the corresponding model is orthotropic, only coefficient in direction 1 of contacted part is taken into account for edge to edge contact. (Integer) |
|
| C1 | Friction law coefficient.
5 (Real) |
|
| C2 | Friction law
coefficient. (Real) |
|
| C3 | Friction law
coefficient. (Real) |
|
| C4 | Friction law
coefficient. (Real) |
|
| C5 | Friction law
coefficient. (Real) |
|
| C6 | Friction law
coefficient. (Real) |
|
| IVIS2 | Interface adhesion flag.
12
(Interger) |
|
| ViscFluid | Viscosity of the fluid at
the interface. 12 (Real) |
|
| SigMaxAdh | Maximum transverse
adhesive stress at interface. 12 (Real) |
|
| ViscAdhFact | Tangential viscous
resistant force scaling factor. 12 (Real) |
|
| Kthe | Conductive heat exchange
coefficient (if fct_IDK = 0). Default = 0.0 (Real) |
|
| Heat exchange scale factor
(if fct_IDK≠ 0) Default = 0.0 (Real) |
||
| fct_IDK | Function identifier for
heat exchange definition with contact pressure. Default = 0 (Integer) |
|
| AscaleK | Abscissa scale factor on
fct_IDK. Default = 1.0 (Real) |
|
| Tint | Interface temperature.
(Real) |
|
| Ithe_form | Heat contact formulation
flag.
(Integer) |
|
| Frad | Radiation factor.
(Real) |
|
| Drad | Maximum distance for
radiation computation. (Real) |
|
| fct_IDc | Function identifier for
the conductive heat exchange coefficient definition as a function of
distance. Default = 0 (Integer) |
|
| Dcond | Maximum distance for
conductive heat exchange. Default = 0.0 (Real) |
|
| Fheats | Frictional heating factor
of secondary. (Real) |
|
| Fheatm | Frictional heating factor
of main. (Real) |
|
| fct_IDF | Friction coefficient with
temperature function identifier. Default = 0 (Integer) |
Flags for Deactivation of Boundary Conditions: IBC
| (1)-1 | (1)-2 | (1)-3 | (1)-4 | (1)-5 | (1)-6 | (1)-7 | (1)-8 |
|---|---|---|---|---|---|---|---|
| IBCX | IBCY | IBCZ |
Definitions
| Field | Contents | SI Unit Example |
|---|---|---|
| IBCX | Deactivation flag of X
boundary condition at impact.
(Boolean) |
|
| IBCY | Deactivation flag of Y
boundary condition at impact.
(Boolean) |
|
| IBCZ | Deactivation flag of Z
boundary condition at impact.
(Boolean) |
Comments
- Contact main/secondary pairs
can be defined in three ways:
- Single self-impacting surface only: surf_ID1 > 0, and surf_ID2 = 0
- Symmetric surface to surface: surf_ID1 > 0, and surf_ID2 > 0
- Nodes to surface: grnd_IDs > 0, surf_ID1 = 0, and surf_ID2 > 0
grnd_IDs > 0 is used to define node to surface contact type, but it may also be used in other contact types. In that case, the node group will be added simply as supplementary secondary nodes, which is useful when users want to add spring element nodes, main node of rigid body, etc. into the contact (as secondary nodes).
If the surface is defined with shells, two contact segments (shifted by half thickness (t)) with opposite normal directions will be generated: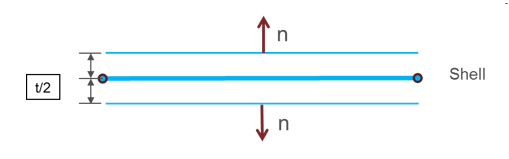
Figure 1.In case of SPMD, each main segment defined by surf_IDi (i=1, 2) must be associated to an element (possibly to a void element).
In cases where quadratic elements are used, it is recommended to define the surfaces by using /SURF/PART/EXT as in that case, middle nodes of quadratic elements are used in the contact treatment.
The surface definition /SURF/PART/ALL is not available with TYPE25.
- Contact stiffness,
is computed as:
(1) Where, depends on Istf:- Istf = 1000,
- Istf = 2,
- Istf = 3,
- Istf = 4,
- Istf = 5,
: main segment stiffness and computed as:- , when the main segment lies on a shell.
- , when main segment lies on a solid.
- , when main segment is shared by shell and solid.
: Secondary node stiffness is an equivalent nodal stiffness considered for interface TYPE25, and computed as:- , when node is connected to a shell element,
- , when node is connected to solid element.
Where,- Segment area
- Volume of the solid
- Bulk modulus
- Thickness of the shell
The Stfac value can be larger than 1.0. There is no limitation value to the stiffness factor (a value larger than 1.0 can reduce the initial time step).
When using /PROP/VOID and /MAT/VOID, material properties and thickness for the VOID material must be entered; otherwise, the contact stiffness of the void elements will be zero. This is especially important if VOID shell elements share elements with solid elements as the stiffness of the shell elements is used in the contact calculation.
- The gap is computed
automatically for each impact as:
- If Igap = 1, variable gap is computed as:
(2) - If Igap=2, variable gap is computed as:
(3) with deactivation of secondary nodes when the element size is smaller than gap values: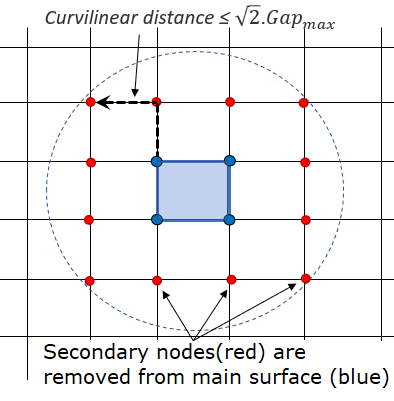
Figure 2.For self-impact contact, when Curvilinear Distance (from a node of the main segment to a secondary node) is smaller than (in initial configuration), this secondary node will not be taken into account by this main segment, and it will not be deleted from the contact for the other main segments.
- If Igap= 3, variable gap is computed as:
(4) Where,-
: main element gap:
, with is the thickness of the main element for shell elements
, for brick elements
-
: secondary node gap:
, if the secondary node is not connected to any element or is only connected to brick or spring elements.
, if the secondary node is connected to a shell element, with being the largest thickness of the shell elements connected to the secondary node.
, if the secondary node is connected to truss or beam elements, with being the cross section of the 1D element.
If the gap modification flag for secondary shell nodes on the free edges Igap0 is set to 1: is reset to zero if the secondary node lies on the free edges of the secondary surface. The gap modification flag for secondary shell nodes on the free edges has no effect if the secondary node is defined through the optional node group (grnod_IDs).
If the secondary node is connected to multiple shells and/or beams or trusses, the largest computed secondary gap is used.
-
: main element gap:
- : length of the smallest edge of the main segment.
-
: if the secondary node belongs to the
main surface,
is the length of the smallest edge of
main segments connected to the secondary node,
=1E+30, otherwise.
In any case, and are limited separately by Gap_max_m and Gap_max_s before the gap is computed.
If the secondary node does not belong to the main surface, the gap remains(5)
- If Igap = 1, variable gap is computed as:
- For node to surface contact,
the gap never extends more than the secondary node gap out of the surface
external border. Ishape
determines if the shape of this gap is square or round and the contact force
(normal) direction. Ishape has
no effect on the gap and its shape for edge to edge contact.Depending on Ishape the gap used for contact at the main surface external border and resulting force direction.
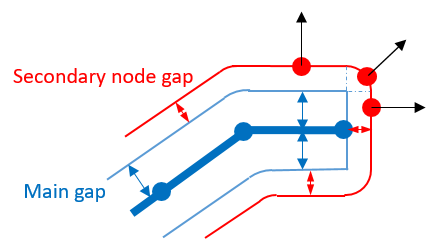
Figure 3. Ishape=1 (Square Gap)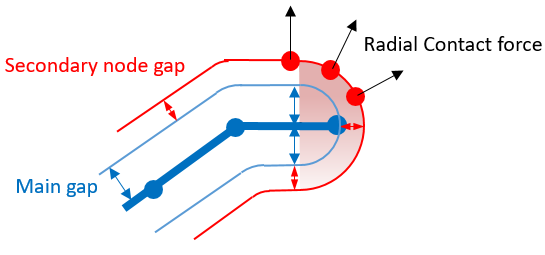
Figure 4. Ishape=2 (Round Gap)Ishape =1 is not available with Igap =3 and will then be reset to Ishape =2.
- For shell element edge to
edge contact, the gap is round. The main side contact gap on the free edge is
shifted so that the edge does not extend out of the shell segment.

Figure 5. Edge contact main sideThe secondary side contact gap on the free edge behavior depends on the value of Igap0 as shown in figure xyz.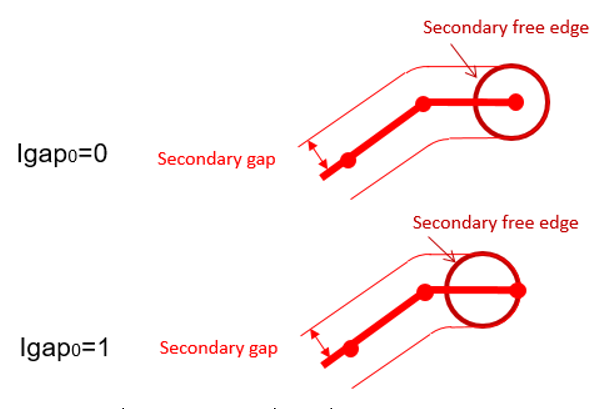
Figure 6. Edge contact secondary side - For solid elements when Iedge=11 and Iedge=13, the secondary side consists of only the sharp edges with angle smaller
than Edge_angle. For Iedge=22, all edges from solid elements are considered on secondary side. On the
main side, all edges from solid elements are included for all 3 Iedge cases.
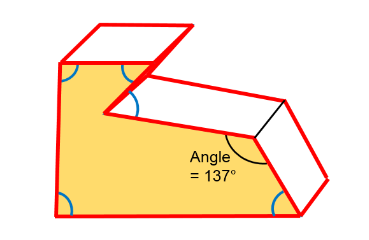
Figure 7. Secondary side edges for Iedge=11 and Iedge=13 - If fric_ID is defined, the contact friction is defined in /FRICTION
and the friction inputs (Ifric, C1, etc.) in this input card are not used.The friction forces are:
(6) While an adhesion force is computed as:
with
Where, is the Coulomb friction coefficient and is defined as:- For flag Ifric by default:
with (Coulomb friction)
- For flag Ifric > 1, new friction
models are introduced. In this case, the friction coefficient is set
by a function:Where,
- Pressure of the normal force on the main segment
- Tangential velocity of the secondary node relative to the main segment
Currently, the coefficients C1 through C6 are used to define a variable friction coefficient for new friction formulations.
The following formulations are available:- Ifric = 1
(Generalized Viscous Friction law):
(7) - Ifric = 2
(Modified Darmstad law):
(8) - Ifric = 3
(Renard law):
if
if
if
Where,- , static coefficient of friction, must be
- , dynamic coefficient of friction, must be
- , maximum coefficient of friction
- , minimum coefficient of friction
- , first critical velocity, must be > 0
- , second critical velocity, must be
- First critical velocity must be less than the second critical velocity .
- The static friction coefficient and the dynamic friction coefficient , must be less than the maximum friction ( and ).
- The minimum friction coefficient
must be less than the
static friction coefficient
and the dynamic friction
coefficient
(
and
).
Table 1. Units for Friction Formulations Ifric Fric C1 C2 C3 C4 C5 C6 1 2 3
- For flag Ifric by default:
- Friction filteringIf Ifiltr = 1, 2 or 3, the tangential forces are smoothed using a filter:
(9) Where, α coefficient is calculated from:- If Ifiltr = 1: α = Xfreq, simple numerical filter
- If Ifiltr = 2: , standard -3dB filter, with , and T = filtering period
- If Ifiltr = 3: , standard -3dB filter, with Xfreq = cutting frequency
The filtering coefficient Xfreq should have a value between 0 and 1.
- Inacti and Ipen_max,
initial penetration treatment:
- Inacti = 1000:
The initial penetrations are ignored: no contact force is applied, but
the nodes are not deactivated from the contact; if the node goes out of
the contact and later gets back into contact, contact forces are then
applied.
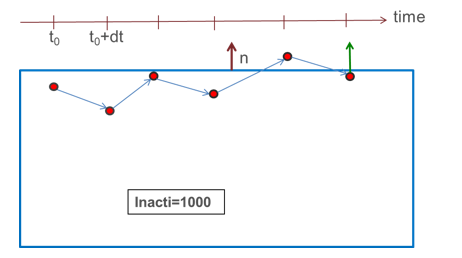
Figure 8. - Inacti = -1: Initial forces are applied on all penetrating nodes. High initial penetrations should be avoided, as they might generate high contact forces and lead to high energy error at the beginning of the computation.
- Inacti = 5: The main segment is shifted by the initial penetration value ( ); therefore, at time zero no initial forces are applied.
The main segment position is restored only in case of rebound larger than .
In the opposite case, when secondary node continues to penetrate, the penetration is computed as:(10) 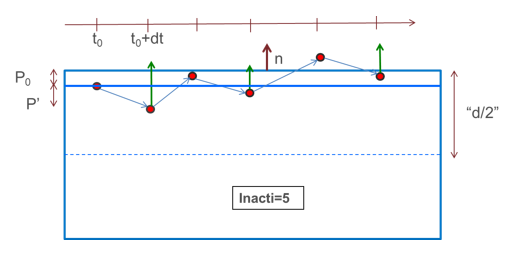
Figure 9.- Intersections and large initial penetration (Inacti= -1 and
5):
Shells: initial intersections should be avoided, as they will lead to wrong direction of contact force and possible secondary nodes anchorage.
- Inacti = 1000:
The initial penetrations are ignored: no contact force is applied, but
the nodes are not deactivated from the contact; if the node goes out of
the contact and later gets back into contact, contact forces are then
applied.
- When sens_ID is defined for activation/deactivation of the interface, Tstart and Tstop are not taken into account.
- For output forces:
When the contact type is asymmetric surface to surface, the output normal contact forces in Time History are calculated correctly, if the two surfaces are well separated.
- IVIS2=-1: is used to add
adhesion in the normal direction and viscous resistive forces in the tangential
direction. This can be used to model thermoplastic composite forming.When used, half of the contact gap is considered an adhesive zone and the other half a physical contact zone. Therefore, to maintain the same physical contact gap, the contact thickness should be doubled using Gap_scale.
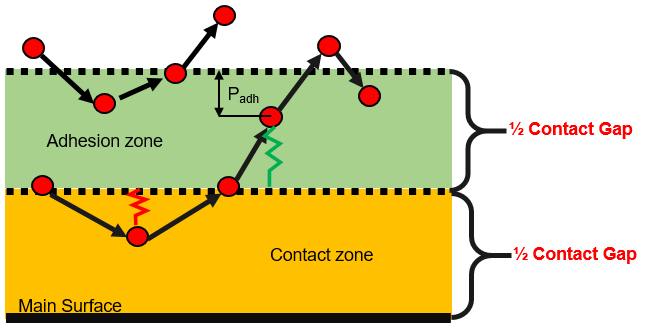
Figure 10.The adhesive force is only applied after secondary nodes have entered the physical contact zone and then move back into the adhesion zone. The adhesive force acts to prevent the node from moving out of the adhesion zone and is applied in the normal direction.(11) Where,- Area of the secondary surface
- Penetration into the adhesion zone
- Contact gap as calculated in Comment 3
The adhesive spring ruptures as the node exits the adhesion zone and will be recreated if the node enters the contact zone again.
Viscous resistive forces are applied in the tangential direction when the secondary nodes enter into the adhesion zone. A viscous tangential opposing force is applied instead of a friction force and is calculated as:(12) Where,- Area of the secondary surface
- Penetration into the adhesion zone
- Contact gap
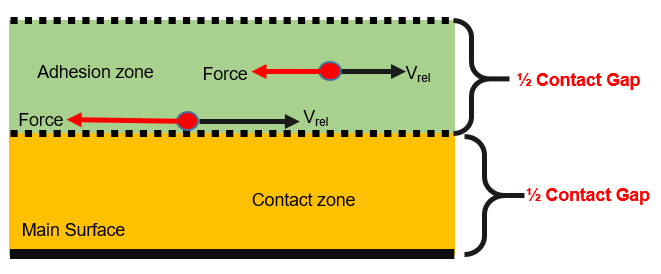
Figure 11. - Heat exchange By Ithe=1 (heat transfer activated) to consider heat exchange and heat friction in contact.
- If Ithe_form=0, then heat exchange is between secondary nodes and constant temperature contact Tint.
- If Ithe_form=1, then heat exchange is between all contact pieces.
In this case Tint is used only when Ithe_form=0. The temperature of the main side is assumed to be constant (equal to Tint). If Ithe_form=1, then Tint is not taken into account. So, the nodal temperature of the main side will be considered.
Contact heat exchange, can involve:- Thermal conduction
Ithe =1 needs the material of the secondary side to be a thermal material using finite element formulation for heat transfer (/HEAT/MAT).
Thermal conduction is computed when the secondary node falls into gap:(13) Heat exchange coefficient- If fct_IDK = 0, then Kthe is heat exchange coefficient and heat exchange depends only on heat exchange surface.
- If fct_IDK ≠ 0, Kthe is a scale factor and heat exchange depends on
contact pressure:
(14) While, is function of fct_IDK.
- Thermal conduction and radiation
When fct_IDc ≠ 0, the heat transfer coefficient can change as function of distance when . In this zone, conductive and radiative heat transfer fluxes are considered.
Abscises and ordinates of this function fct_IDc must be between 0 and 1.
The heat transfer coefficient is computed as:(15) The maximum value of is equal to the value of Kthe when Kthe is constant. Otherwise, in case of Kthe depending on pressure, the maximum is equal to value of Kthe for contact pressure . drops to zero when distance is equal to Dcond.
- Thermal radiation Radiation is considered in contact if and the distance, , of the secondary node to the main segment is:
(16) While Drad is the maximum distance for radiation computation. The default value for Drad is computed as the maximum of:- upper value of the Gap (at time 0) among all nodes
- smallest side length of secondary element
Note: It is recommended not to set the value too high for Drad, which may reduce the performance of Radioss Engine.A radiant heat transfer conductance is computed as:(17) with(18) Where,- Stefan Boltzman constant.
- Emissivity of secondary surface.
- Emissivity of main surface.
- Heat friction Frictional energy can be converted into heat when Ithe > 0 for interface.
- Fheats is defined as the fraction of this energy which is converted into heat and transferred to the secondary side.
- Fheatm is defined as the fraction of this energy which is converted into heat and transferred to the secondary side.
The frictional heat is defined for a stiffness formulation:(19)