/INTER/TYPE19
Block Format Keyword This is a combination of two symmetric TYPE7 interfaces and one TYPE11 interface, with common input based on the same secondary/main surfaces. Secondary node group for interface TYPE7, as well as secondary and main line segments used by equivalent TYPE11 interface are virtually generated from these input surfaces.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /INTER/TYPE19/inter_ID/unit_ID | |||||||||
| inter_title | |||||||||
| surf_IDs | surf_IDm | Istf | Ithe | Igap | Iedge | Ibag | Idel | Icurv | |
| Fscalegap | Gapmax | ||||||||
| Stmin | Stmax | %mesh_size | dtmin | Irem_gap | Irem_i2 | ||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| node_ID1 | node_ID2 |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| Stfac | Fric | Gapmin | Tstart | Tstop | |||||
| IBC | Inacti | VISs | VISF | Bumult | |||||
| Ifric | Ifiltr | Xfreq | Iform | sens_ID | fric_ID | ||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| C6 | |||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| Kthe | fct_IDK | Tint | Ithe_form | AscaleK | |||||
| Frad | Drad | Fheats | Fheatm | ||||||
Definitions
| Field | Contents | SI Unit Example |
|---|---|---|
| inter_ID | Interface identifier. (Integer, maximum 10 digits) |
|
| unit_ID | Unit Identifier. (Integer, maximum 10 digits) |
|
| inter_title | Interface title. (Character, maximum 100 characters) |
|
| surf_IDs | Secondary surface
identifier. (Integer) |
|
| surf_IDm | Main surface
identifier. (Integer) |
|
| Istf | Stiffness definition flag. 8
(Integer) |
|
| Ithe | Heat contact flag. 25
(Integer) |
|
| Igap | Gap/element option flag. 6
7
(Integer) |
|
| Iedge | Edges to edge contact flag. 24
(Integer) |
|
| Ibag | Airbag vent holes closure flag in case
of contact.
(Integer) |
|
| Idel | Node and segment deletion flag. 5
(Integer) |
|
| Icurv | Secondary gap with curvature. 11
12
13
(Integer) |
|
| Fscalegap | Gap scale factor (used only when Igap = 3). Default = 1.0 (Real) |
|
| Gapmax | Maximum gap (used only when Igap = 3).
(Real) |
|
| Stmin | Minimum stiffness. (Real) |
|
| Stmax | Maximum stiffness. Default = 1030 (Real) |
|
| %mesh_size | Percentage of mesh size (used only when
Igap = 3). Default = 0.4 (Real) |
|
| dtmin | Minimum interface time step. 23
(Real) |
|
| Irem_gap | Flag for deactivating secondary nodes or
lines, if element size < gap value, in case of self-impact contact. 15
(Integer) |
|
| Irem_i2 | Flag for deactivating the secondary
node, if the same contact pair (nodes) has been defined in
/INTER/TYPE2.
|
|
| node_ID1 | First node
identifier. (Integer) |
|
| node_ID2 | Second node
identifier. (Integer) |
|
| Stfac | Interface stiffness (if Istf = 1). Default = 1.0 (Real) |
|
| Stiffness scale factor for the interface
(if Istf ≠ 1). Default = 0.0 (Real) |
||
| Fric | Coulomb friction. (Real) |
|
| Gapmin | Minimum gap for impact activation. 7 (Real) |
|
| Tstart | Start time. (Real) |
|
| Tstop | Time for temporary
deactivation. (Real) |
|
| IBC | Deactivation flag of boundary conditions
at impact. (Boolean) |
|
| Inacti | Deactivation flag of stiffness in case
of initial penetrations. 14
(Integer) |
|
| VISs | Critical damping coefficient on
interface stiffness. Default set to 0.05 (Real) |
|
| VISF | Critical damping coefficient on
interface friction. Default set to 1.0 (Real) |
|
| Bumult | Sorting factor. Default set to 0.20 (Real) |
|
| Ifric | Friction formulation flag. 19
20 Only used if fric_ID is not defined.
(Integer) |
|
| Ifiltr | Friction filtering flag. 21
(Integer) |
|
| Xfreq | Filtering coefficient. 21
(Real) |
|
| Iform | Friction penalty formulation type.
(Integer) |
|
| sens_ID | Sensor identifier to activate/deactivate
the interface. 2
If an identifier sensor is defined, the activation/deactivation of interface is based on sensor and not with Tstart or Tstop. (Integer) |
|
| fric_ID | Friction identifier for friction
definition for selected pairs of parts.
(Integer) |
|
| C1 | Friction law
coefficient. (Real) |
|
| C2 | Friction law
coefficient. (Real) |
|
| C3 | Friction law
coefficient. (Real) |
|
| C4 | Friction law
coefficient. (Real) |
|
| C5 | Friction law
coefficient. (Real) |
|
| C6 | Friction law
coefficient. (Real) |
|
| Kthe | Heat exchange coefficient (if fct_IDK = 0) . Default = 0.0 (Real) |
|
| Heat exchange scale factor (if fct_IDK ≠ 0). Default = 1.0 (Real) 25 |
||
| fct_IDK | Function identifier for thermal heat
exchange definition with contact pressure. Default = 0 (Integer) |
|
| Tint | Interface temperature. 25 (Real) |
|
| Ithe_form | Heat contact formulation flag.
(Integer) |
|
| AscaleK | Abscissa scale factor on fct_IDK. Default = 1.0 (Real) |
|
| Frad | Radiation factor. 27 (Real) |
|
| Drad | Maximum distance for radiation
computation. (Real) |
|
| Fheats | Frictional heating factor of secondary.
26 (Real) |
|
| Fheatm | Frictional heating factor of
main. (Real) |
Flags for Deactivation of Boundary Conditions: IBC
| (1)-1 | (1)-2 | (1)-3 | (1)-4 | (1)-5 | (1)-6 | (1)-7 | (1)-8 |
|---|---|---|---|---|---|---|---|
| IBCX | IBCY | IBCZ |
Definitions
| Field | Contents | SI Unit Example |
|---|---|---|
| IBCX | Deactivation flag of X boundary
condition at impact.
(Boolean) |
|
| IBCY | Deactivation flag of Y boundary
condition at impact.
(Boolean) |
|
| IBCZ | Deactivation flag of Z boundary
condition at impact.
(Boolean) |
Comments
- The contact main and secondary
surfaces and be defined in the following ways.Single surface self-impacting and edge to edge self-impacting contact:
- surf_IDs > 0 and surf_IDm = 0
- surf_IDs = 0 and surf_IDm > 0
Symmetric surface to surface and edge to edge contact- surf_IDs > 0 and surf_IDm > 0
- When sens_ID is defined for activation/deactivation of the interface, Tstart and Tstop are not taken into account.
- In case of SPMD, each main segment defined by surf_IDm must be associated to an element (possibly to a void element).
- For flag Ibag, refer to the monitored volume option (Monitored Volumes (Airbags)).
- Flag Idel = 1 has a CPU cost higher than Idel = 2.
- Variable gap is computed as:
- If Igap = 1:
(1) - If Igap = 3:
(2) - If Igap = 4:Node to surface contact uses variable gap
(3) For self-contact, if element size < gap value, then secondary nodes are deactivated for nearby main segments. This is the same as using /INTER/TYPE7, Irem_gap = 2. Edge to edge contact uses a constant gap as defined by Gapmin.
-
Where,
-
- : main element gap
- , with thickness of the main element for shell elements
-
- : secondary node gap:
- = 0 if the secondary node is not connected to any element or is only connected to brick or spring elements.
-
- : length of the smaller edge of element
- If the secondary node is connected to multiple shells and/or beams or trusses, the largest computed secondary gap is used.
-
- If Igap = 1:
- A default value for Gapmin is computed as:
(4) While,- Main surface gap
- Average thickness of the main elements for shell elements
- Average side length of the main brick elements
- Smallest side length of all main segments (shell or brick)
- Secondary surface gap.
- Contact stiffness:For node to 3-node and 4-node segments or 2-node segments to 2-node segments contacts computation as:
(5) Where,-
is computed from both main segment stiffness
and secondary node stiffness
:
Istf = 2,
Istf = 3,
Istf = 4,
Istf = 5,
-
is main segment stiffness and computed as:When main segment lies on a shell or is shared by shell and solid:
(6) When main segment lies on a solid:(7) Where,- Segment area
- Volume of the solid
- Bulk modulus
-
is an equivalent nodal stiffness considered for
interface TYPE7, and computed as:When node is connected to a shell element:
(8) When node is connected to solid element:(9)
There is no limitation value to the stiffness factor Stfac (but a value can be larger than 1.0 to reduce the initial time step).
When using /PROP/VOID and /MAT/VOID, material properties and thickness for the VOID material must be entered; otherwise, the contact stiffness of the void elements will be zero. This is especially important if VOID shell elements share elements with solid elements as the stiffness of the shell elements is used in the contact calculation.
-
is computed from both main segment stiffness
and secondary node stiffness
:
- The values given in Line 4 are ignored, if Igap ≠ 3.
- The values given in Line 5 are ignored, if Istf ≤ 1.
- Spherical curvature (Icurv = 1) is defined with node_ID1 (center of the sphere).
- The node_ID2 given in Line 6 is ignored, if Icurv = 1.
- Cylindrical curvature (Icurv = 2) is defined with node_ID1 and node_ID2 (on the axis of the cylinder).
- Inacti = 3 may create initial
energy if the node belongs to a spring element.Inacti = 6 is recommended instead of Inacti =5, to avoid high frequency effects into the interface.
Figure 1. - With Irem_gap = 2, it allows to have the element size smaller than gap values:
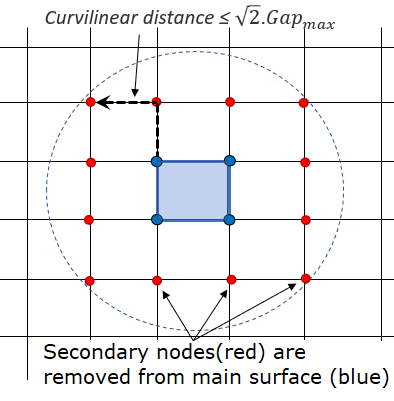
Figure 2. Secondary nodes removed from node to surface contact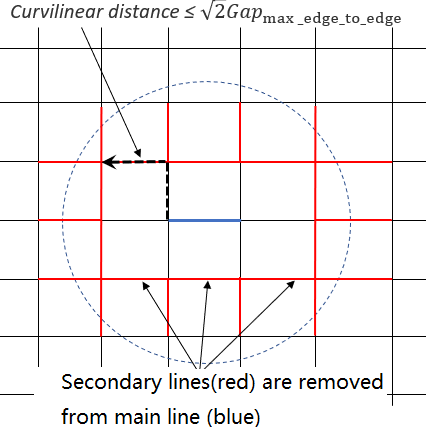
Figure 3. Secondary lines removed from edge to edge contactIn case of self-impact contact, when Curvilinear is smaller than (in initial configuration), then this secondary entity (node / line) will not be taken into account by this main entity (surface / line). The secondary entity will not be deleted from the contact for other other main entities. This also applies both nodes to surface and edge to edge contact as stated in the /INTER/TYPE7 and /INTER/TYPE11 comments.
- The sorting factor, Bumult is used to speed up the sorting algorithm.
- The sorting factor, Bumult is machine dependent.
- One node can belong to the two surfaces at the same time.
- If fric_ID is
defined, the contact friction is defined in /FRICTION and the friction
inputs (Ifric, C1,
etc.) in this input card are not used.For friction formulation:
- Whatever the friction flag Ifric, the Coulomb friction coefficient
used in the TYPE11 interface is:
(10) - The friction flag Ifric only applies to the TYPE7 interface(s).
- If the friction flag Ifric = 0 (default), the
old static friction formulation is used:
(11) While, with is Coulomb Friction coefficient.
- For flag Ifric > 0, new friction
models are introduced. In this case, the friction coefficient is set by a function
.Where,
- Pressure of the normal force on the main segment
- Tangential velocity of the secondary node relative to the main segment
- Whatever the friction flag Ifric, the Coulomb friction coefficient
used in the TYPE11 interface is:
- Currently, the coefficients C1 through C6 are used to define a variable friction
coefficient
for
new friction formulations.
- Ifric = 1 (Generalized
Viscous Friction law):
(12) - Ifric = 2 (Modified Darmstad
law):
(13) - Ifric = 3 (Renard law):
if
if
if
Where, - First critical velocity must be different to 0 ( ).
- First critical velocity must be lower than the second critical velocity ( ).
- The static friction coefficient and the dynamic friction coefficient , must be less than the maximum friction ( and ).
- The minimum friction coefficient , must be less than the static friction coefficient and the dynamic friction coefficient ( and ).
Table 1. Units for Friction Formulations Ifric Fric C1 C2 C3 C4 C5 C6 1 2 3 - Ifric = 1 (Generalized
Viscous Friction law):
- Friction filtering:If Ifiltr ≠ 0, the tangential forces are smoothed using a filter:
(14) Where α coefficient is calculated from:- If Ifiltr= 1: , simple numerical filter.
- If Ifiltr = 2: , standard -3dB filter, with , and is filtering period.
- If Ifiltr = 3:
, standard -3dB filter, with
is cutting frequency.
The filtering coefficient should have a value between 0 and 1.
- Friction penalty formulation Iform
- If Iform = 1, (default) viscous
formulation, the friction forces are:
(15) While an adhesion force is computed as:
with
- If Iform = 2, stiffness
formulation, the friction forces are:
(16) While an adhesion force is computed as:
with
Where, is the tangential velocity of the secondary node relative to the main segment.
- If Iform = 1, (default) viscous
formulation, the friction forces are:
- If the time step of a secondary node in this contact becomes less than dtmin, the secondary node is deleted from the contact and a warning message is printed in the output file. This dtmin value takes precedence over any model interface minimum time step entered in /DT/INTER/DEL.
- Edges to edge contact flag Iedge:
- Iedge = 1: only external
edges are generated from contact surfaces which defined by SHELL parts, it is
recommended for optimized performance. Cannot be used when the surface contains only
solid parts which lead to an empty line and then error message will be printed.
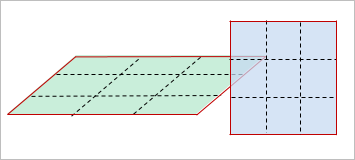
Figure 4. - Iedge = 2: all edges are
generated from contact surfaces.
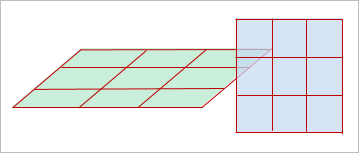
Figure 5.
- Iedge = 1: only external
edges are generated from contact surfaces which defined by SHELL parts, it is
recommended for optimized performance. Cannot be used when the surface contains only
solid parts which lead to an empty line and then error message will be printed.
- Heat exchange:By Ithe =1 (heat transfer activated) to consider heat exchange and heat friction in contact.
- If Ithe_form = 0, then heat exchange is between shell and constant temperature contact Tint.
- If Ithe_form = 1, then heat exchange is between all contact pieces.
Tint is used only when Ithe_form= 0. In this case, the temperature of main side assumed to be constant (equal to Tint). If Ithe_form=1, then Tint is not taken into account, for the nodal temperature of main side will be considered.
Heat exchange coefficient:- If fct_IDK = 0, then Kthe is heat exchange coefficient and heat exchange depends only on heat exchange surface.
- If fct_IDK ≠ 0, then Kthe is a scale factor and the heat exchange
will depend on the contact pressure:
(17) - While is the function of fct_IDK.
- Heat Friction:
- Frictional energy is converted into heat when Ithe > 0 for interface.
- Fheats and
Fheatm are defined as the
fraction of frictional energy and distributed respectively to the secondary side and
main side. So generally:
(18) When both Fheats and Fheatm are equal to 0, the conversion of the frictional sliding energy to heat is not activated.
- The frictional heat QFric is
defined:
- If Iform= 2 (a stiffness
formulation):Secondary side:
(19) Main side:(20) (Ithe_form= 1) - If Iform= 1 (a penalty
formulation):Secondary side:
(21) Main side:(22) (Ithe_form= 1)
- If Iform= 2 (a stiffness
formulation):
- Radiation:Radiation is considered in contact if and the distance, , of the secondary node to the main segment is:
(23) While is the maximum distance for radiation computation. The default value for is computed as the maximum of:- Upper value of the Gap (at time 0) among all nodes
- Smallest side length of secondary element
It is recommended not to set the value too high for , which may reduce the performance of Radioss Engine.
A radiant heat transfer conductance is computed as:(24) with(25) Where,- Stefan Boltzman constant
- Emissivity of secondary surface
- Emissivity of main surface
