Turbulent Flow Past a Convex Curve in a Channel
In this application, AcuSolve is used to simulate fully developed turbulent flow through a channel containing a convex curve in the lower wall. AcuSolve results are compared with experimental results as described in Smits (1979) and on the NASA Langley Research Center Turbulence Modeling Resource webpage. The close agreement of AcuSolve results with experimental data and reference turbulence model performance validates the ability of AcuSolve to model cases with turbulent flow moving past a convex curved wall.
Problem Description
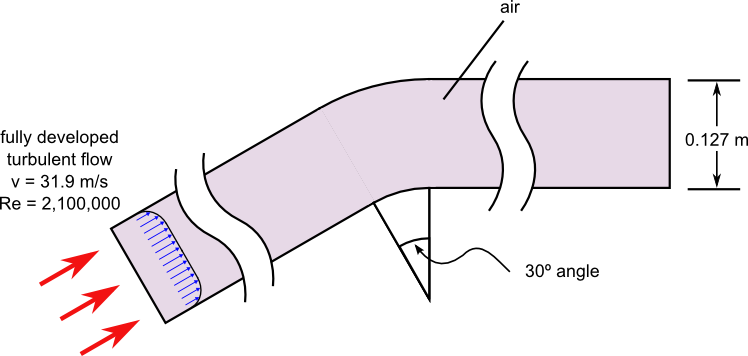
Figure 1. Critical Dimensions and Parameters for Simulating Turbulent Flow Through a Convex Channel
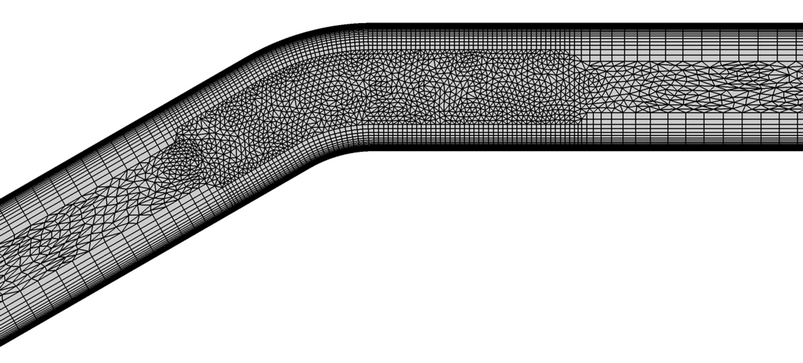
Figure 2. Detail of the Mesh used for Simulating Turbulent Flow Through a Convex Channel
AcuSolve Results
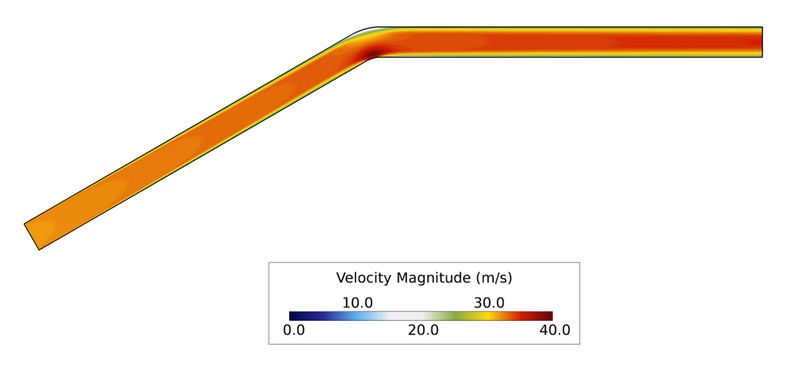
Figure 3. Velocity Contours in the Streamwise Plane
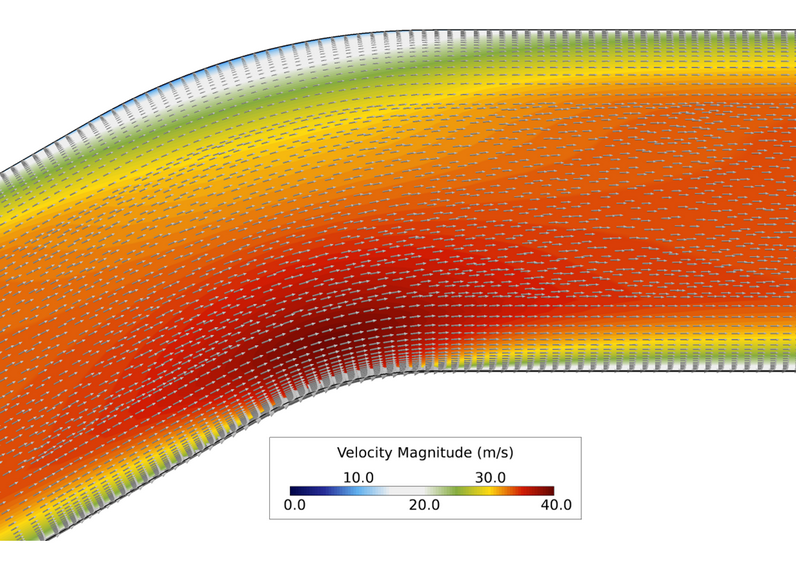
Figure 4. Close up View of Velocity Vectors and Velocity Contours at the 30° Bend
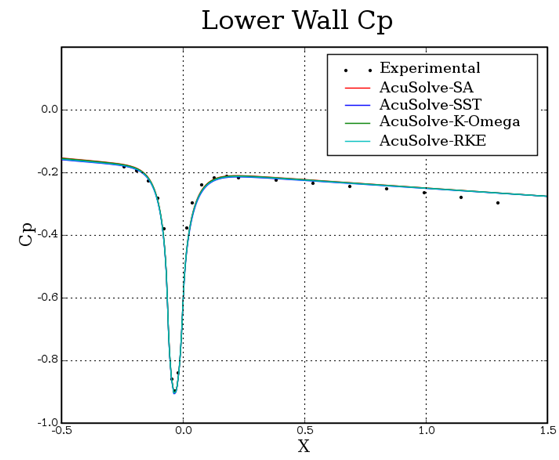
Figure 5. Coefficient of Pressure Plotted Against Relative Distance Along the Lower Wall from the Curve
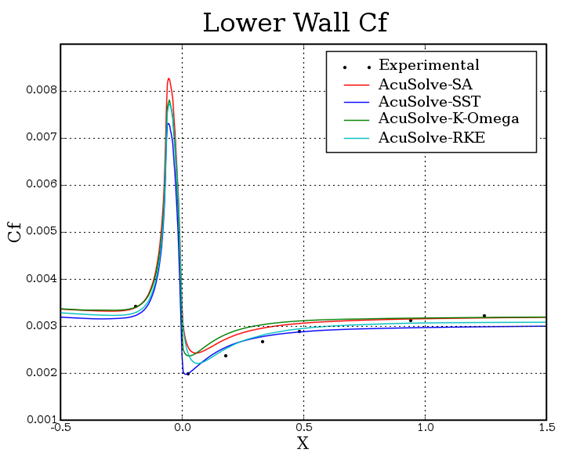
Figure 6. Skin Friction Coefficient Plotted Against Relative Distance Along the Lower Wall from the Curve
Summary
In this application, a turbulent flow through a curved channel at a Reynolds number of 2,100,000 is simulated and compared against experimental data. The AcuSolve results compare well with the experimental data for pressure coefficient and skin friction coefficient within the channel. The performance of the Spalart Allmaras turbulence model was found to be consistent with previously published results for flow through a convex-curved channel (NASA 2015) and the SST turbulence model appears to predict the shear stress on the lower wall most accurately. AcuSolve demonstrates the ability to predict the complex boundary layers resulting from the curvature of the channel and accurately predicts the propagation of the flow further downstream.
Simulation Settings for Turbulent Flow past a Convex Curve in a Channel
AcuConsole database file: <your working directory>\convex_curvature_turbulent\convex_curvature_turbulent.acs
Global
- Problem Description
- Analysis type - Steady State
- Turbulence equation - Spalart Allmaras
- Auto Solution Strategy
- Max time steps - 100
- Convergence tolerance - 0.0001
- Relaxation factor - 0.4
- Material Model
- Fluid
- Density - 1.225 kg/m3
- Viscosity - 1.8603e-5 kg/m-sec
Model
- Fluid
- Volumes
- Fluid - elbow
- Element Set
- Material model - Fluid
- Element Set
- Fluid - inlet
- Element Set
- Material model - Fluid
- Element Set
- Fluid - outlet
- Element Set
- Material model - Fluid
- Element Set
- Fluid - elbow
- Surfaces
- -Y
- Simple Boundary Condition
- Type - Slip
- Simple Boundary Condition
- +Y
-
- Type - Slip
-
- Inlet
- Simple Boundary Condition
- Type - Inflow
- Inflow type - Velocity
- Inflow velocity type - Normal
- Normal velocity - 31.9 m/sec
- Turbulence input type - Direct
- Eddy viscosity - 1.3671e-7 m2/sec
- Simple Boundary Condition
- -Y
- Internal
- Simple Boundary Condition - (disabled)
- Lower Wall
- Simple Boundary Condition
- Type - Wall
- Turbulence wall type - Low Reynolds Number
- Simple Boundary Condition
- Outlet
- Simple Boundary Condition
- Type - Outflow
- Simple Boundary Condition
- Upper Wall
- Simple Boundary Condition
- Type - Wall
- Turbulence wall type - Low Reynolds Number
- Simple Boundary Condition
References
A. J. Smits, S. T. B. Young, and P. Bradshaw. "The Effect of Short Regions of High Surface Curvature on Turbulent Boundary Layers". Journal of Fluid Mechanics. 94(2):209-242. 1979
NASA Langley Research Center Turbulence Modeling Resource webpage. http://turbmodels.larc.nasa.gov/smitscurve_val.html. Accessed May 2015.