/IMPDISP

Block Format Keyword Defines imposed displacements on a group of nodes.

Format

Field	Contents	SI Unit Example
`impdisp_ID`	Imposed displacement block identifier. (Integer, maximum 10 digits)
`unit_ID`	Unit Identifier. (Integer, maximum 10 digits)
`impdisp_title`	Imposed displacement block title. (Character, maximum 100 characters)
`fct_ID`_T	Time function identifier. (Integer)
`Dir`	Direction: X, Y, and Z in translation; XX, YY, and ZZ in rotation. (Text)
`Skew_ID`	Skew identifier. (Integer)
`sens_ID`	Sensor identifier. ≠ 0 (sensor activated) The imposed displacement is applied at time of sensor activation and function is shifted in time. (Integer)
`grnd_ID`	Node group on which the imposed displacement is applied. (Integer)
`icoor`	Coordinate system usage type. = 0 Cartesian coordinates. = 1 Cylindrical coordinates. (Integer)
`Ascale`_x	Abscissa (time) scale factor for `fct_ID`_T. Default = 1.0 (Real)	$[s]$
`Fscale`_Y	Ordinate (displacement) scale factor for `fct_ID`_T. Default = 1.0 (Real)	$[m]$ or $[rad]$
`T`_start	Start time. (Real)	$[s]$
`T`_stop	Stop time. Default = 10³⁰ (Real)	$[s]$

The displacement direction must be right justified in the ten characters of field number 2.
If T_start and T_stop are specified, the displacement is imposed between these times, but the time versus displacement function is not shifted to begin at T_start.
When a sensor is defined sens_ID, the imposed displacement is applied at the time of sensor activation and the function is shifted by the sensor activation time.
When a sensor sens_ID is used with T_start and T_stop, the imposed displacement will only occur if the sensor activation time occurs between T_start and T_stop.
The Ascale_X and Fscale_Y are used to scale the abscissa (time) and ordinate (displacement or angle).
The actual load function value is calculated as:(1)
$F (t) = F s c a l e_{y} \cdot f_{T} (\frac{t}{A s c a l e_{x}})$

Where, $f_{T}$ is the function of fct_ID_T.
If icoor=1, the directions X, Y, and Z (resp. XX, YY, and ZZ) refer to translations along (resp. rotations around) the radial direction (r), azimuthal angular direction ( $θ$ ) and longitudinal direction (Z) (/SKEW/FIX).

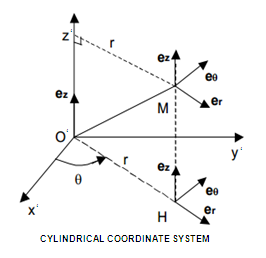
Figure 1.
If icoor=1 when imposing the translational displacement in the radial, resp. the azimuthal direction, the displacement of the node is set so that:(2)
$δ_{r} (t) = \int \dot{r} d t = F s c a l e_{y} \cdot f_{T} (\frac{t}{A s c a l e_{x}})$
(3)
$r e s p . θ = \int \dot{θ} d t = F s c a l e_{y} \cdot f_{T} (\frac{t}{A s c a l e_{x}})$

Where, $f_{T}$ is the function of fct_ID_T.