/RWALL
Block Format Keyword Defines the following types of rigid walls: Infinite Plane, Infinite Cylinder, Sphere and Parallelogram.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /RWALL/type/rwall_ID/unit_ID | |||||||||
| rwall_title | |||||||||
| node_ID | Slide | grnd_ID1 | grnd_ID2 | ||||||
| Dsearch | fric | ffac | ifq | ||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| XM | YM | ZM | |||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| Mass | VX0 | VY0 | VZ0 | ||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| XM1 | YM1 | ZM1 | |||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| XM2 | YM2 | ZM2 | |||||||
Definitions
| Field | Contents | SI Unit Example |
|---|---|---|
| type | Rigid wall type
keyword (see table below) |
|
| rwall_ID | Rigid wall
identifier (Integer, maximum 10 digits) |
|
| unit_ID | Unit Identifier (Integer, maximum 10 digits) |
|
| rwall_title | Rigid wall
title (Character, maximum 100 characters) |
|
| node_ID | Node identifier (moving
rigid wall) (Integer) |
|
| Slide | Sliding flag.
(Integer) |
|
| grnd_ID1 | Node group defining
secondary nodes to be added to the rigid
wall. (Integer) |
|
| grnd_ID2 | Node group defining
secondary nodes to be deleted from the rigid
wall. (Integer) |
|
| Dsearch | Distance for secondary
search. (Real) |
|
| fric | Friction. (Real) |
|
| Diameter of the
sphere. (Real) |
||
| ffac | Filtering factor. The default value depends on the ifq flag (Real) |
|
| ifq | Filtering flag. 5
Default = 0 (Integer) |
|
| XM | X coordinate of
M (Real) |
|
| YM | Y coordinate of
M (Real) |
|
| ZM | Z coordinate of
M (Real) |
|
| Mass | Mass of the rigid wall.
8 If no mass is entered, the rigid wall will have a constant imposed velocity. (Real) |
|
| VX0 | Initial velocity in X
direction (Real) |
|
| VY0 | Initial velocity in Y
direction (Real) |
|
| VZ0 | Initial velocity in Z
direction (Real) |
|
| XM1 | X coordinate of
M1 (Real) |
|
| YM1 | Y coordinate of
M1 (Real) |
|
| ZM1 | Z coordinate of
M1 (Real) |
|
| XM2 | X coordinate of
M2 (Real) |
|
| YM2 | Y coordinate of
M2 (Real) |
|
| ZM2 | Z coordinate of
M2 (Real) |
Rigid Wall Type
- Type
- Description
- PLANE
- plane
- CYL
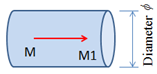
- Cylinder of diameter
- SPHER
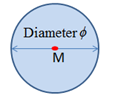
- Sphere of diameter
- PARAL
- Parallelogram
Surface Input Type
- Type
- Description
- PLANE
- MM1 defines the normal direction
- CYL
- MM1 defines the axis of the cylinder
- SPHER
- M is the center of the sphere
- PARAL
- and define the parallelogram
Comments
- The first input defines the rigid wall coordinates of one point M or a node_ID in case of moving rigid wall.
- The next input is the coordinate of a point M1 and possibly a point M2 (in case of a moving wall, M1 and M2 have the same motion as node_ID).
- The secondary nodes to a rigid wall can be defined as a group of nodes and/or as nodes initially at a distance less than the distance (Dsearch) from the rigid wall.
- The friction filtering option is only available for a slide rigid wall with friction (Slide =2).
- Filtering flag
ifg
If ifq ≠ 0, the tangential (friction) forces in each secondary node in contact are filtered using a simple rule:
(1) Where,- Filtered tangential force.
- Calculated tangential force at time t before filtering.
- Filtered tangential force at the previous time step
- Current simulation time
- Current simulation time step
- Filtering coefficient
The flag ifq defines a method for filtering, α coefficient.
If ifq =1, filtering coefficient is directly input by you:
If ifq =2, α corresponds to a 3dB filtering level for user-defined frequency (frequency defined in terms of time step number):(2) with , and
If ifq =3, α corresponds to a 3dB filtering level for user-defined frequency:(3) Where,- Time step
- ffac
- The sphere (SPHER) and parallelogram
(PARAL) are not infinite. For parallelograms, the normal is defined
using:
(4) and the diameter of the sphere is defined using .
- Nodal thickness of rigid wall secondary nodes is not taken into account.
- For moving rigid walls with MASS=0 or blank, the rigid wall will have a constant imposed velocity and not an initial velocity.