/FAIL/HC_DSSE
Block Format Keyword Strain-based Ductile Failure Model: Hosford-Coulomb with Domain of Shell-to-Solid Equivalence. A nonlinear strain based failure criteria for shells with linear damage accumulation.
The failure strain is described by the Hosford-Coulomb function (refer to /FAIL/EMC for solids). Works only with elasto-plastic material number > 28. This failure criteria was developed by Keunhwan Pack (Massachusetts Institute of Technology MIT) and Dirk Mohr (Swiss Federal Institute of Technology ETH Zurich). 1
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /FAIL/HC_DSSE/mat_ID/unit_ID | |||||||||
| Ifail_sh | P_thickfail | I-Flag | |||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| a | b | c | d | ||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| c2 | c3 | c4 | Inst_str | ||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| fail_ID |
Definitions
| Field | Contents | SI Unit Example |
|---|---|---|
| mat_ID | Material identifier (Integer, maximum 10 digits) |
|
| unit_ID | Unit Identifier (Integer, maximum 10 digits) |
|
| Ifail_sh | Shell failure flag.
(Integer) |
|
| P_thickfail | Percentage of through thickness
integration points that must fail before the element is deleted. (shells
only). Default = 1.0 (Real) |
|
| I-Flag | Input type flag.
(Integer) |
|
| a | Failure model parameter
a. (Real) |
|
| b | Failure model parameter
b. (Real) |
|
| c | Failure model parameter
c. (Real) |
|
| d | Failure model parameter
d. (Real) |
|
| c2 | Failure strain in pure shear
(triaxiality
). (Real) |
|
| c3 | Failure strain in uniaxial tension
(triaxiality
). (Real) |
|
| c4 | Failure strain in plane strain tension
(triaxiality =
). (Real) |
|
| Inst_str | Instability strain in plane strain
tension for localized necking. (Real) |
|
| Parameter
. Default = 0.1 (Real) |
||
| fail_ID | Failure criteria
identifier. (Integer, maximum 10 digits) |
Example
This example uses the HC-DSSE parameter input (a, b, c, d parameters with I-Flag = 0).
⇔
and one use physical input (failure strain input with I-Flag=1). HC-DSSE parameters a, b, c, d will be calculated using a curve fit by the Radioss Starter.
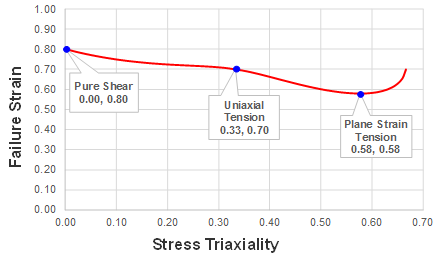
Figure 1.
Example (HC-DSSE Parameter Input)
#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
# MUNIT LUNIT TUNIT
kg mm ms
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 1. MATERIALS:
/MAT/PLAS_TAB/2/1
DP600 from SSAB Homepage
# RHO_I
7.8E-6 0
# E Nu Eps_p_max Eps_t Eps_m
210 .3 0 0 0
# N_funct F_smooth C_hard F_cut Eps_f
1 0 0 0 0
# fct_IDp Fscale Fct_IDE EInf CE
0 0 0 0 0
# func_ID1 func_ID2 func_ID3 func_ID4 func_ID5
14
# Fscale_1 Fscale_2 Fscale_3 Fscale_4 Fscale_5
1
# Eps_dot_1 Eps_dot_2 Eps_dot_3 Eps_dot_4 Eps_dot_5
0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FAIL/HC_DSSE/2/1
# Ishell P_thickfail I_Flag
1 .5 0
# a b c d n_f
1.742 0.7 0.029 1.6 0.1
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/14
Mat_Curev Quasi-static DOCOL DP 600 (Material from SSAB Homepage 2010)
# X Y
0 .306
.00112 .415
.00218 .445
.003 .461
.00404 .474
.00517 .489
.00613 .498
.0071 .505
.00806 .512
.00901 .522
.0102 .53
.0121 .543
.013 .55
.014 .555
.015 .561
.0159 .567
.0171 .572
.0181 .577
.0204 .592
.0303 .632
.0405 .663
.0502 .687
.06 .706
.0702 .722
.0807 .737
.09 .749
.0997 .758
.101 .759
.11 .768
.15000001 .805
.2 .84
.30000001 .9
.5 1
1 1.21
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#enddata
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|Example (Physical Input)
#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
# MUNIT LUNIT TUNIT
kg mm ms
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 1. MATERIALS:
/MAT/PLAS_TAB/2/1
DP600 from SSAB Homepage
# RHO_I
7.8E-6 0
# E Nu Eps_p_max Eps_t Eps_m
210 .3 0 0 0
# N_funct F_smooth C_hard F_cut Eps_f
1 0 0 0 0
# fct_IDp Fscale Fct_IDE EInf CE
0 0 0 0 0
# func_ID1 func_ID2 func_ID3 func_ID4 func_ID5
14
# Fscale_1 Fscale_2 Fscale_3 Fscale_4 Fscale_5
1
# Eps_dot_1 Eps_dot_2 Eps_dot_3 Eps_dot_4 Eps_dot_5
0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FAIL/HC_DSSE/2/1
# Ishell P_thickfail I_Flag
1 .5 1
# c2 c3 c4 Inst_str n_f
0.8 0.7 0.58 0.1 0.1
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/14
Mat_Curev Quasi-static DOCOL DP 600 (Material from SSAB Homepage 2010)
# X Y
0 .306
.00112 .415
.00218 .445
.003 .461
.00404 .474
.00517 .489
.00613 .498
.0071 .505
.00806 .512
.00901 .522
.0102 .53
.0121 .543
.013 .55
.014 .555
.015 .561
.0159 .567
.0171 .572
.0181 .577
.0204 .592
.0303 .632
.0405 .663
.0502 .687
.06 .706
.0702 .722
.0807 .737
.09 .749
.0997 .758
.101 .759
.11 .768
.15000001 .805
.2 .84
.30000001 .9
.5 1
1 1.21
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#enddata
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|Comments
- This failure criterion is defined in
the space of equivalent plastic strain at failure versus stress triaxiality (state of
stress) for plane stress condition. This allows for definition of failure strain that
varies with different loading conditions. It consists of two curves. One is the fracture
locus (that is, below the red curve) and the other is the localized necking locus (blue
curve).
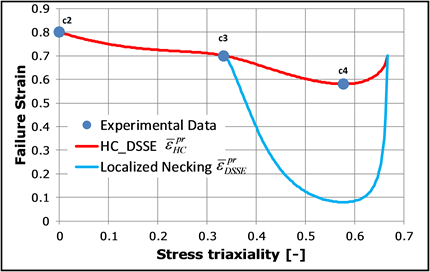
Figure 2.The former takes the following form:(1) , and are functions of the Lode angle :
The latter is defined only between uniaxial and eqi-biaxial tension conditions for ( ) in which localized necking can occur.(2) (3) - The universal exponent of =0.01 is used.
- Localized necking is predicted in a non-local manner when all integration points or layers have > 1.
- The failure curve parameters a, b,
c, and d, must be calibrated based on test
results.
is the triaxiality.
- Alternatively, switching the I-Flag to 1, allows Radioss to do the parameter fit internally.
- No shell fracture in compression area ( ).
- Damage is calculated as:
(4)