Iform = 4
Block Format Keyword This boundary can simulate gas inlet conditions for multi-material ALE laws (formulation: Iform = 0, 1, 10, or 11).
The boundary sub-material states is calculated from a state at a stagnation point which is provided by the user. When using this feature, it is no longer necessary to use imposed velocity (/IMPVEL) where the velocity is computed by numerical scheme.
Description
Where, . It can be deduced that .
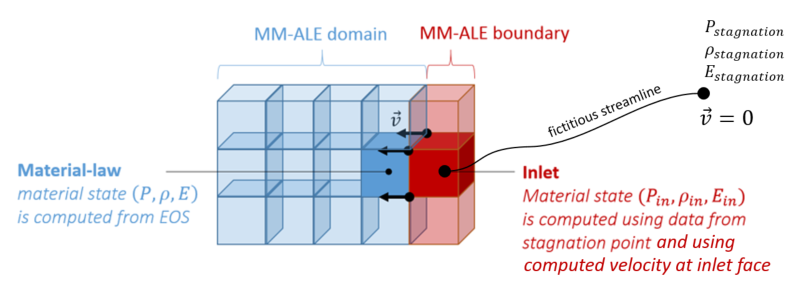
Figure 1.
Format
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| /MAT/LAW51/mat_ID/unit_ID | |||||||||
| mat_title | |||||||||
| Blank Format | |||||||||
| Iform | |||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| Scaletime | PEXT | ||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| fct_IDα1 | fct_ID 1 | fct_IDE1 | |||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| fct_IDα2 | fct_ID 2 | fct_IDE2 | |||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| fct_IDα3 | fct_ID 3 | fct_IDE3 | |||||||
Definitions
| Field | Contents | SI Unit Example |
|---|---|---|
| mat_ID | Material identifier. (Integer, maximum 10 digits) |
|
| unit_ID | Unit Identifier. (Interger, maximum 10 digits) |
|
| mat_title | Material title. (Character, maximum 100 characters) |
|
| Iform | Formulation flag.
(Integer) |
|
| Scaletime | Abscissa scale factor for input
functions. 2 Default = 1 (Real) |
|
| PEXT | External (ambient) pressure. 3 (Real) |
|
| Initial volumetric fraction. 4 (Real) |
||
| Initial density at stagnation point.
1 (Real) |
||
| Initial energy at stagnation point.
5 (Real) |
||
| fct_IDαi | (Optional)
Volumetric fraction scaling function.
identifier. 6
(Integer) |
|
| fct_ID i | (Optional)
Density fraction scaling function.
identifier
(Integer) |
|
| fct_IDEi | (Optional)
Energy fraction scaling function.
identifier.
(Integer) |
|
| Coefficient for perfect gas EOS. 5 (Real) |
||
| Perfect gas (
) constant. 5 (Real) |
||
| Coefficient for perfect gas EOS. 5 (Real) |
Comments
- The provided stagnation point
is used to compute gas inlet state. Bernoulli theorem is applied:
(2) This leads to gas inlet state:(3) (4) (5) Then the global material state is determined by computing a mean value:- Pressure
- Density
- Energy
- The optional scaling functions can be used such to scale the volumetric, density or energy fractions.
- Parameter
enables you to take ambient pressure into account in case
you want to work with relative pressure
. This parameter is required by Radioss for correct energy integration at each cycle. Otherwise,
numerical EOS solving is generally incorrect. It represents pressure which must be added
to EOS calculation to obtain total (physical) pressure. It has no influence on pressure
contour in animation files.
Example using linear EOS:
Total Pressure: and also
Relative Pressure: , and also
- Volumetric fractions enable the sharing of elementary volume within the three
different materials.
For each material, must be defined between 0 and 1.
Sum of initial volumetric fractions must be equal to 1.
For automatic initial fraction of the volume, refer to /INIVOL.
- Perfect gas EOS is
. Generally it can be written using this general form
, where
. This provides more flexibility, depending on whether
pressure and energy are total or relative:
(6) Where, and .
This leads to usual form from .(7) Where, , and .(8) Where, , and .
-
flag is the minimum value for the computed pressure.
Since , defining implies and .
The materials pressure must remain positive to avoid any tensile strength, then, leads .
For solid materials, the default value for is suitable.
- EOS parameters must be consistent with gas EOS from adjacent MM-ALE domain.