FR Card
The FR card sets the frequency/frequencies (in Hz), at which the solution will be obtained.
On the Source/Load tab, in the Settings
group, click the ![]() Frequency (FR)
icon.
Frequency (FR)
icon.
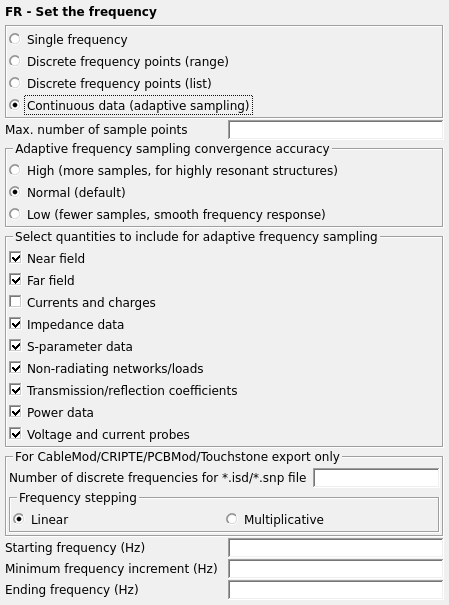
Figure 1. The FR - Set the frequency dialog.
The solution can be done for a single frequency, a range of discrete frequencies (linear or multiplicative stepping), a list of discrete frequencies or a continuous solution in a given frequency band with adaptive frequency interpolation with the option to set the convergence accuracy. For a continuous solution, only one FR card is allowed. Specific quantities of interest to the user may also be selected to be included for adaptive sampling. Unselected quantities will be calculated at the discrete solution frequency points.
Parameters:
- Single frequency
- Only a single frequency will be analysed.
- Discrete frequency points (range)
- If this item is selected the following parameters are applicable:
- Number of frequency points
- For a discrete frequency range sweep, the number of frequency samples must be larger than 1.
- Frequency scale
- In this group either Linear or Multiplicative scaling is selected. If Linear is selected, then consecutive frequencies differ with a fixed value, for example, the new frequency is the previous value plus the frequency increment. If Multiplicative is selected, then consecutive frequencies differ by a constant factor, for example, the new frequency is the previous value multiplied by the frequency factor.
- Specify by
- If Frequency increment/factor is selected, the user specifies the increment or factor mentioned in the previous item. Thus, the number of frequencies and the start frequency then determine the ending frequency. If Ending frequency is selected, the user specifies this and the increment/factor is calculated.
- Discrete frequency points (list)
- If this item is selected, the following parameters are applicable:
- Number of discrete frequencies
- For a list of discrete frequency sweep, the number of frequency samples must be larger than 1. The list of discrete frequencies is applicable when a list of frequencies is required which is not linearly or logarithmically spaced.
- Continuous data (adaptive sampling)
- Select interpolate this item to use an adaptive frequency
interpolation technique to obtain a continuous representation of the results in the
given frequency band. When using this feature, the remaining parameters have the
following meaning:
- Max. number of sample points
- Maximum number of discrete frequency points in this frequency band at which Feko may be executed (limitation to avoid convergence problems). If left empty, the default value of 1000 will be used.
- Adaptive frequency sampling convergence accuracy
- This allows the user to manually set the adaptive frequency sampling convergence accuracy. Note that the default setting should be used for most cases, but in special cases where a structure with many resonances is being modelled a higher convergence accuracy should be used.
- Select quantities to include for adaptive frequency sampling
- The quantities selected will be included in the adaptive frequency sampling.
- For CableMod/CRIPTE/PCBMod/Touchstone export only, Number of discrete frequencies for .isd /.snp file
- This field is only relevant when the CM or SP card is used to create an .isd or .snp file respectively. The results are written to the .isd or .snp file for the number of discrete frequencies specified in this field.
- Starting frequency (Hz)
- Defines the start frequency of the simulation range.
- Ending frequency (Hz)
- Defines the end frequency of the simulation range.
- Minimum frequency increment (Hz)
- Minimum increment between adaptive samples, see the note below.
In order to obtain a continuous frequency response, the adaptive frequency interpolation technique obtains the solution at a set of discrete frequency points. They are automatically placed, for example using large frequency increments in regions with a smooth behaviour of the results, and much finer frequency increments close to resonances. Sometimes, for example when using a frequency dependent mesh, the Feko results versus frequency may contain small discontinuities. In these cases the adaptive algorithm cannot converge. (It will continue to refine the frequency increment as it tries to fit a smooth curve through the discontinuity and will only stop when the Max. number of sample points is reached.) One may avoid this by setting the Frequency increment to the minimum allowable separation distance between neighbouring frequency sample points. The value of the Frequency increment must be smaller than the resolution required to solve, for example, sharp resonances. If left empty, the default is:
- for a linear frequency scale (additive increments):
(2) - for a multiplicative frequency scale (multiplicative increments):
(3)
When writing results at discrete frequencies to a .isd file, the frequency increment when a linear frequency scale is used is calculated similar to the case for as shown above.
If more than one frequency is to be examined, then all the control cards up to the next FR card or EN card will be read into a buffer and are executed for each frequency.