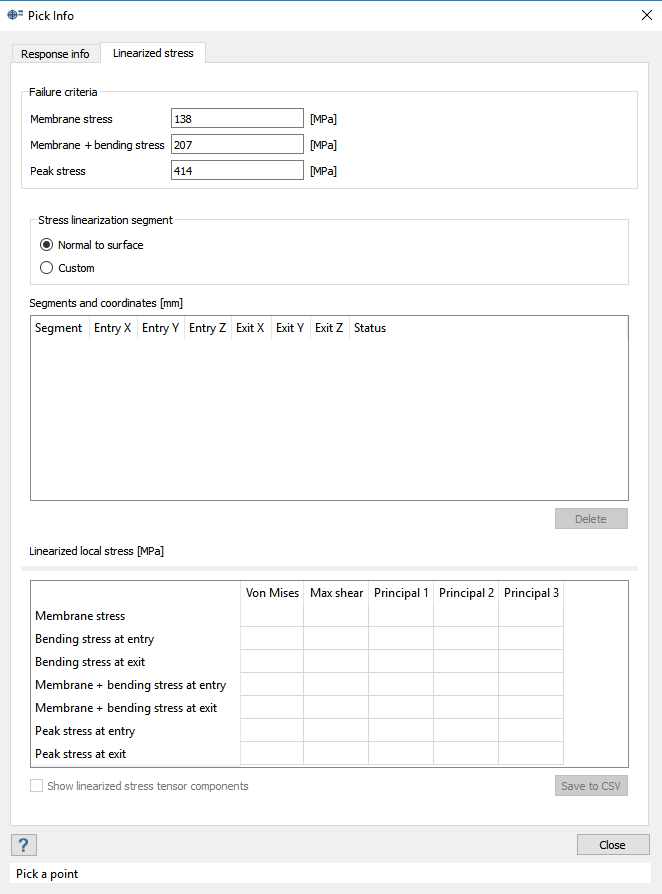
From the extracted stress values above, the average membrane stress tensor +
bending stress tensors at the entry and exit points are calculated using
numerical integration.
= ith component of
membrane stress
= ith component of
extracted stress value
= ithcomponent of
bending stress at the entry
= ith component of
bending stress at the exit
L = Length of the Stress linearization
segment
x = position of a point along the segment
Peak stress and membrane and bending stress are also calculated at the entry
and exit.
= ith component of
peak stress at the entry
= ith component of
peak stress at the exit