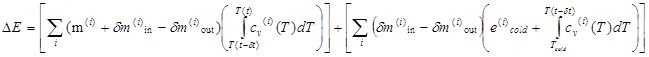Energy Variation Within a Time Step

Let $T (t - δ t)$ the temperature, $P (t - δ t)$ the pressure, and $V (t - δ t)$ the volume of the airbag at time $t - δ t$ , and $m^{(i)}$ the mass of gas $i$ at time $t - δ t$ . $T (t)$ , $P (t)$ , $V (t)$ are respectively temperature, pressure and volume of the airbag at time $t$ , and $m^{(i)} + δ m_{in}^{(i)} - δ m_{out}^{(i)}$ the mass of gas $i$ at time $t$ .

Using , the variation of total gas energy can be written as:(1)

Δ E = [\sum_{i} (m^{(i)} + δ m^{(i)}_{in} - δ m^{(i)}_{out}) (e^{(i)}_{c o l d} + \int_{T_{c o l d}}^{T (t)} c_{v}^{(i)} (T) d T)] - [\sum_{i} m^{(i)} (e^{(i)}_{c o l d} + \int_{T_{c o l d}}^{T (t - δ t)} c_{v}^{(i)} (T) d T)]

which can be written as: (2)

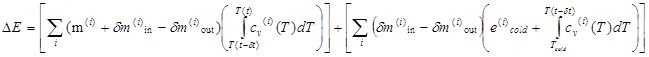
On the other hand, the basic energy equation Thermodynamical Equations, Equation 1 of the airbag and the expression of enthalpy in Thermodynamical Equations, Equation 5 gives:(3)

\begin{array}{l} Δ E = [\sum_{i} δ m^{(i)}_{i n} (e^{(i)}_{c o l d} + \frac{R}{M^{(i)}} T^{(i)}_{i n} + \int_{T_{c o l d}}^{T^{(i)}_{i n}} c_{v}^{(i)} (T) d T)] - \\ [\sum_{i} δ m^{(i)}_{o u t} (e^{(i)}_{c o l d} + \frac{R}{M^{(i)}} T^{(i)}_{o u t} + \int_{T_{c o l d}}^{T^{(i)}_{o u t}} c_{v}^{(i)} (T) d T)] - δ W \end{array}

Where, $δ m_{in}^{(i)}$ and $T^{(i)}_{i n}$ are characteristics of the inflator and are considered as input to the problem. $δ m_{out}^{(i)}$ and $T^{(i)}_{o u t}$ can be estimated from the velocity at vent hole $u (t)$ . $δ W$ is the variation of the external work. This estimation will be described hereafter.

It comes from Equation 1 and Equation 2:(4)

\begin{array}{l} \sum_{i} (m^{(i)} + δ m^{(i)}_{i n} - δ m^{(i)}_{o u t}) \int_{T (t - δ t)}^{T (t)} c_{v}^{(i)} (T) d T = \\ [\sum_{i} δ m_{i n}^{(i)} (\frac{R}{M^{(i)}} T^{(i)}_{i n} + \int_{T (t - δ t)}^{T_{i n}^{(i)}} c_{v}^{(i)} (T) d T)] - [\sum_{i} δ m_{o u t}^{(i)} (\frac{R}{M^{(i)}} T_{o u t}^{(i)} + \int_{T (t - δ t)}^{T_{o u t}^{(i)}} c_{v}^{(i)} (T) d T)] - δ W \end{array}

The variation of the external work can be written as:(5)

δ W = \frac{(P (t) + P (t - δ t))}{2} (V (t) - V (t - δ t))

Using Thermodynamical Equations, Equation 9, the last expression can be written as:(6)

δ W = \frac{1}{2} (\frac{[\sum_{i} \frac{m^{(i)} + δ m^{(i)}_{i n} - δ m^{(i)}_{o u t}}{M^{(i)}}] R T (t)}{V (t)} + \frac{[\sum_{i} \frac{m^{(i)}}{M^{(i)}}] R T (t - δ t)}{V (t - δ t)}) (V (t) - V (t - δ t))

The last equation can be introduced to Equation 4:(7)

\begin{array}{l} [\sum_{i} (m^{(i)} + δ m^{(i)}_{i n} - δ m^{(i)}_{o u t}) \int_{T (t - δ t)}^{T (t)} c_{v}^{(i)} (T) d T] + [\sum_{i} \frac{m^{(i)} + δ m^{(i)}_{i n} - δ m^{(i)}_{o u t}}{M^{(i)}}] R T (t) \frac{V (t) - V (t - δ t)}{2 V (t)} \\ = [\sum_{i} δ m^{(i)}_{i n} (\frac{R}{M^{(i)}} T^{(i)}_{i n} + \int_{T (t - δ t)}^{T^{(i)}_{i n}} c_{v}^{(i)} (T) d T)] - [\sum_{i} δ m^{(i)}_{o u t} (\frac{R}{M^{(i)}} T^{(i)}_{o u t} + \int_{T (t - δ t)}^{T^{(i)}_{o u t}} c_{v}^{(i)} (T) d T)] - \\ [\sum_{i} \frac{m^{(i)}}{M^{(i)}}] R T (t - δ t) \frac{V (t) - V (t - δ t)}{2 V (t - δ t)} \end{array}

The first order approximation

\int_{T (t - δ t)}^{T (t)} c_{v}^{(i)} (T) \approx c_{v}^{(i)} (T_{| t - δ t}) (T (t) - T (t - δ t))

for each gas, which allows rewrite Equation 7 as:(8)

\begin{array}{l} [\sum_{i} (m^{(i)} + δ m^{(i)}_{i n} - δ m^{(i)}_{o u t}) c_{v}^{(i)} (T_{| t - δ t}) (T (t) - T (t - δ t))] + \\ [\sum_{i} \frac{m^{(i)} + δ m^{(i)}_{i n} - δ m^{(i)}_{o u t}}{M^{(i)}}] R T (t) \frac{V (t) - V (t - δ t)}{2 V (t)} \\ = [\sum_{i} δ m^{(i)}_{i n} (\frac{R}{M^{(i)}} T^{(i)}_{i n} + \int_{T (t - δ t)}^{T^{(i)}_{i n}} c_{v}^{(i)} (T) d T)] - [\sum_{i} δ m^{(i)}_{o u t} (\frac{R}{M^{(i)}} T_{o u t} + \int_{T (t - δ t)}^{T^{(i)}_{o u t}} c_{v}^{(i)} (T) d T)] - \\ [\sum_{i} \frac{m^{(i)}}{M^{(i)}}] R T (t - δ t) \frac{V (t) - V (t - δ t)}{2 V (t - δ t)} \end{array}

Which allows to determine the actual temperature $T (t)$ . The actual pressure then computed from the equation of perfect gas (Thermodynamical Equations, Equation 9).