AIRBAG1

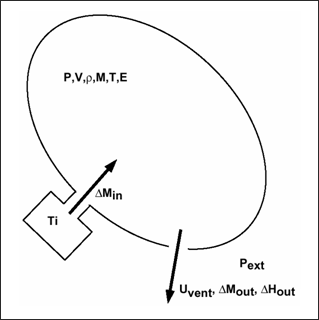
Uniform pressure is assumed inside the volume. Perfect gas law and adiabatic conditions are assumed. Injected mass (or mass flow rate) and temperature are defined as a time function using the injector property. A sensor can define the inflator starting time.

The deflation of the vent hole occurs after reaching a pressure (

P_{d e f}

) or time (

t_{d e f}

) criteria.

Numerical Damping

Viscosity, $μ$ can be used to reduce numerical oscillations.

If $μ$ =1, a critical damping (shell mass and volume stiffness) is used. A viscous pressure, $q$ is computed as:

$q = - \frac{μ}{A} \sqrt{\frac{P A ρ t}{V}} \frac{d V}{d t}$ if $\frac{d V}{d t} < 0$

$q = 0$ if $\frac{d V}{d t} > 0$

Where,

$t$: Fabric thickness
$ρ$: Density of the fabric
$A$: Bag surface

The applied pressure is:(1)

P - P_{e x t} + q

Initial Conditions

To avoid initial disequilibrium and mathematical discontinuity for zero mass or zero volume, the following initial conditions are set at time zero (I_equil =0) or at the beginning of jetting (if I_equil =1).

$P_{e x t} = P_{i n i}$ external pressure
$T_{0} = T_{i n i}$ initial temperature (295K by default)
If the initial volume is less than $10^{- 4} A^{\frac{3}{2}}$ , a constant small volume is added to obtain an initial volume: $V_{i n i} = 10^{- 4} A^{\frac{3}{2}}$
Initial mass, energy and density are defined from the above values.

There is no need to define an injected mass at time zero.

Gases Definition

Initial and injected gas is defined with /MAT/GAS. Four types of gas (MASS, MOLE, PREDEF, or CSTA) could be defined. Then the specific capacity per unit mass at constant pressure for the gas is:
- MASS type(2)
  $C_{p} = (C_{p a} + C_{p b} T + C_{p c} T^{2} + C_{p d} T^{3} + \frac{C_{p e}}{T^{2}} + C_{p f} T^{4})$
- MOLE type(3)
  $C_{p} = \frac{1}{M W} (C_{p a} + C_{p b} T + C_{p c} T^{2} + C_{p d} T^{3} + \frac{C_{p e}}{T^{2}})$
  
  Where, $M W$ is the molecular weight of the gas.
- CSTA type
  User input $C_{p}$ and $C_{V}$ with the unit of $[\frac{J}{k g K}]$ .
- PREDEF type
  About 14 commonly used gases (N2, O2, Air, etc) predefined in Radioss.
Injected gas
N_jet defines the number of injectors by monitored volume. The material of the injected gas is defined with /MAT/GAS. The injector properties (/PROP/INJECT1 or /PROP/INJECT2) define the injected mass curve defined fct_ID_M and injected temperature curve defined fct_ID_T.
Injected mass curve and injection temperature can be obtained:
- From the airbag manufacturer
- From a tank test
sens_ID is the sensor number to start injection.
Jetting effect I_jet is used only for /MONVOL/AIRBAG1 or /MONVOL/COMMU1
If I_jet ≠ 0, the jetting effect is modeled as an overpressure $Δ P_{j e t}$ applied to elements of the bag.(4)
$Δ P_{j e t} = Δ P (t) \cdot Δ P (θ) \cdot Δ P (δ) \cdot \max (n \cdot m, 0)$

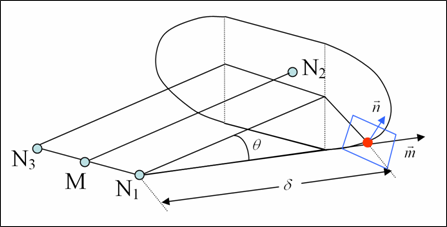
Figure 2.

N₁, N₂, and N₃ are defined based on the injector geometry (refer to the Radioss Starter Input Manual)

$Δ P (t), Δ P (θ), Δ P (δ)$ are empirical functions provided by the user via $f c t_I D_{P t}$ , $f c t_I D_{P θ}$ , and $f c t_I D_{P δ}$

Vent Hole Definition

N_vent defines the number of vent holes used.

$s u r f_I D_{v}$ is the surface identifier defining the vent hole

A_vent is the vent area (if $s u r f_I D_{v} = 0$ ) or a scale factor ( $s u r f_I D_{v}$ ≠ 0)

B_vent = 0 (if $s u r f_I D_{v} = 0$ ) or a scale factor on the impacted surface ( $s u r f_I D_{v}$ ≠ 0)

T_stop is a stop time for venting

T_start is the time at which leakage starts

$Δ P_{d e f}$ is the relative vent deflation pressure

$Δ t P_{d e f}$ is the time duration during which $Δ P > Δ P_{d e f}$

f c t_I D_{v}

is the function identifier

f_{P} (P - P_{e x t})

for Chemkin model (I_form=2)(5)

v e n t_h o l e s_s u r f a c e = A_{v e n t} \cdot A_{n o n_i m p a c t e d} \cdot f_{t} (t) \cdot f_{P} (P - P_{e x t}) \cdot f_{A} (\frac{A_{n o n_i m p a c t e d}}{A_{0}})

f c t_I D_{v} \neq 0

, the outflow velocity,

v

is defined by Chemkin as:(6)

v = F s c a l e_{v} f_{v} (P - P_{e x t})

Where, $F s c a l e_{v}$ is the scale factor of the function $f c t_I D_{v}$ .

and the outgoing mass is computed as:(7)

{\dot{m}}_{o u t} = ρ \cdot A_{v e n t} \cdot f_{v} (P - P_{e x t}) \cdot F s c a l e_{v}

Or, with the conservation of enthalpy between airbag and vent hole, adiabatic conditions and unshocked flow, it is then possible to express outgoing mass flow through vent holes as a function of

P_{e x t}

ρ

P_{v e n t}

u_{v e n t}

and

A_{v e n t}

.(8)

{\dot{m}}_{o u t} = ρ_{v e n t} \cdot A_{v e n t} \cdot u = ρ {(\frac{P_{e x t}}{P})}^{\frac{1}{γ}} \cdot A_{v e n t} \cdot u

In the case of supersonic outlet flow, the vent pressure,

P_{v e n t}

is equal to external pressure,

P_{e x t}

for unshocked flow. For shocked flow,

P_{v e n t}

is equal to critical pressure,

P_{c r i t}

and velocity,

u

is bounded to critical sound speed:(9)

u^{2} < \frac{2}{γ + 1} c^{2} = \frac{2 γ}{γ + 1} \frac{P}{ρ}

and(10)

P_{c r i t} = P {(\frac{2}{γ + 1})}^{\frac{γ}{γ - 1}}

(11)

P_{v e n t} = \max (P_{c r i t} ​, P_{e x t} ​)

The outgoing mass flow of gas

i

is:(12)

{\dot{m}}_{o u t}^{(i)} = \frac{V^{(i)}}{V} {\dot{m}}_{o u t}

Where,

V^{(i)}

is the volume occupied by gas

i

and satisfies:(13)

V^{(i)} = \frac{n^{(i)}}{n} V

from $P V^{(i)} = n^{(i)} R T$ and $P V = [\sum_{i} n^{(i)}] R T$ .

Then,(14)

{\dot{m}}_{o u t}^{(i)} = \frac{n^{(i)}}{\sum_{i} n^{(i)}} {\dot{m}}_{o u t}

Porosity

The isenthalpic model is also used for porosity. In this case, you can define the surface for outgoing flow:(15)

A_{e f f} = C_{p s} \cdot A r e a_{p s}

or, (16)

A_{e f f} = C_{p s} (t) \cdot {Area}_{p s} (P - P_{e x t})

Where,

$C_{p s} (t)$: Function of fct_ID_cps
${Area}_{p s} (P - P_{e x t})$: Function of fct_ID_aps

It is also possible to define closure of the porous surface when contacts occurs by defining the interface option I_bag=1.