Periodic Boundary Condition (PBC)
Use a periodic boundary condition (PBC) to analyse infinite periodic structures. A typical application of PBC is to analyse frequency selective surface (FSS) structures.
The unit-cell definition for the periodic boundary condition solution is based on vectors. For the one-dimensional case, the start point and end point of a single vector are required. Periodicity is defined based on two planes passing through these start point and end point, and normal to the vector formed between them. The vector used to define one-dimensional periodicity can have any orientation but must have a non-zero length.
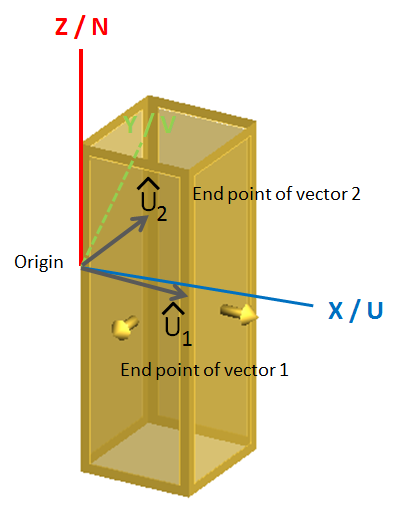
Figure 1. The periodic boundary condition for two-dimensional periodicity.
For array modelling using periodic boundary conditions, the beam (squint) angle is specified by defining the theta and phi angle. The phase along the periodic lattice vectors is computed automatically to ensure the specified beam direction.