Specifies an emissivity model for the radiation equation.
Description
This command specifies an ideal grey-surface emissivity model for the radiation equation. This
model is only applicable to radiation surfaces, and is not used for the
radiation_heat_flux variable in the
ELEMENT_BOUNDARY_CONDITION command.
EMISSIVITY_MODEL commands are referenced by
RADIATION_SURFACE
commands:
EMISSIVITY_MODEL( "my emissivity model" ) {
type = constant
emissivity = 0.5
}
RADIATION_SURFACE( "hot wall" ) {
emmissivity_mdoel = "my emmissivity model"
...
}
The emissivity is the factor
in
the Stefan-Boltzmann law for the total emissive power of an ideal grey
surface:
(1)
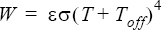
where
is the Stefan-Boltzmann constant, given by the
Stefan_boltzmann_constant parameter of the
RADIATION command; T is the
temperature; and Toff is the offset to convert
to an absolute temperature, given by the absolute_temperature_offset
parameter of the EQUATION command.
A constant emissivity model applies a spatially constant emissivity, as in the above example.
Emissivity models of types
piecewise_linear and
cubic_spline
may be used to define emissivity as a function of a single independent variable. For
example,
EMISSIVITY_MODEL( "curve fit emissivity model" ) {
type = piecewise_linear
curve_fit_values = { 273, 0.2 ; 323, 0.2 ; 373, 0.3 ; 423, 0.4 ; }
curve_fit_variable = temperature
}
defines emissivity as a function of temperature. In general, the problem must contain the
variable defined by curve_fit_variable; this is not an issue here since
radiation problems always contain temperature. The curve_fit_values
parameter is a two-column array corresponding to the independent variable and the emissivity
values. The independent variable values must be in ascending order. The limit point values
of the curve fit are used when curve_fit_variable falls outside of the
curve fit limits.
The
curve_fit_values data may be read from a file. For the above example,
the curve fit values may be placed in a file, such as
emissivity.fit:
273 0.2
323 0.2
373 0.3
423 0.3
and read
by:
EMISSIVITY_MODEL( "curve fit emissivity model" ) {
type = piecewise_linear
curve_fit_values = Read( "emissivity.fit" )
curve_fit_variable = temperature
}
An emissivity of type user_function may be used to model more complex
behaviors; see the AcuSolve User- Defined Functions
Manual for a detailed description of user-defined functions.
For example, consider an emissivity that is equal to 0.5 between temperatures of 300 and 400, and
0.3 otherwise. The input command may be given
by:
EMISSIVITY_MODEL( "UDF emissivity model" ) {
type = user_function
user_function = "usrEmissivityExample"
user_values = { 300, # lower temp. limit of band
400, # upper temp. limit of band
0.3, # default emissivity
0.5 } # emissivity in temperature band
}
where the user-defined function
"usrEmissivityExample" may be implemented as
follows:
#include "acusim.h"
#include "udf.h"
UDF_PROTOTYPE( usrEmissivityExample ) ; /* function prototype */
Void usrEmissivityExample (
UdfHd udfHd, /* Opaque handle for accessing data */
Real* outVec, /* Output vector */
Integer nItems, /* Number of elements */
Integer vecDim /* = 1 */
) {
Integer elem ; /* an element counter */
Real temp0 ; /* lower temp. limit of band */
Real temp1 ; /* upper temp. limit of band */
Real eDef ; /* default emissivity */
Real eBand ; /* emissivity in temperature band */
Real* temp ; /* temperature */
Real* usrVals ; /* user values */
udfCheckNumUsrVals( udfHd, 4 ) ; /* check for error */
usrVals = udfGetUsrVals( udfHd ) ; /* get the user vals */
temp0 = usrVals[0] ; /* lower temp */
temp1 = usrVals[1] ; /* upper temp */
eDef = usrVals[2] ; /* default emissivity */
eBand = usrVals[3] ; /* band emissivity */
temp = udfGetRsfData( udfHd, UDF_RSF_TEMPERATURE ) ; /* get the temp. */
for ( elem = 0 ; elem < nItems ; elem++ ) {
if ( temp[elem] >= temp0 && temp[elem] <= temp1 ) {
outVec[elem] = eBand ;
} else {
outVec[elem] = eDef ;
}
}
} /* end of usrEmissivityExample() */
The dimension of the returned emissivity vector, outVec, is the number of
elements.
The
multiplier_function parameter may be used to uniformly scale the
emissivity values. The value of this parameter refers to the user-given name of a
MULTIPLIER_FUNCTION command in the input file. For example, a ramped
emissivity may be specified
by:
EMISSIVITY_MODEL( "ramped emissivity model" ) {
type = constant
emissivity = 0.4
multiplier_function = "ramped"
}
MULTIPLIER_FUNCTION( "ramped" ) {
type = piecewise_linear
curve_fit_values = { 1, 0.1 ; 10, 1 }
curve_fit_variable = time_step
}
The diffused fraction defines the proportion of reflected radiation intensity at a surface
which is diffused, i.e., the reflection may also have a specular component. If the radiation
intensity reflection coefficient at the surface is defined by
(2)
then the diffused reflection coefficient,
, is defined in terms of the diffused fraction (
) and the emissivity of the surface by
(3)
and the specular reflection coefficient by
(4)
If
, then the reflection at the surface is
completely diffused. If
then the reflection is
specular. The outgoing radiation intensity,
, at
the surface in terms of the above two reflection coefficients is given by
(5)
Michael Modest, Radiative Heat Transfer, Third Edition
(2013)where the first terms represent emission from the surface, the second term the diffused
component incoming radiation heat flux and the third the specular component. The diffused
component represents a sum over all radiation intensities along ordinates that are incident
to the surface (i.e. a hemisphere of incoming radiation to the surface);
is the normal into the domain and
the jth ordinate direction. The ordinate
direction (
), the total number of ordinate directions (
) and the weights (
) are automatically defined by the order of the
radiation_quadrature (S2, S4, S6, S8 & S10). The specular
ordinate direction (
) is the direction that the radiation intensity must strike the
surface to reflect in a specular fashion along the outgoing ordinate direction,
, and is given by
(6)
which means the angle that incident radiation intensity strikes the surface equals the
angle of reflection.
To enable specular reflection a RADIATION_SURFACE must be defined and
the diffused fraction,
, and emissivity,
, must both be less than one.
For
example,
RADIATION_SURFACE( "wall" ) {
…
emissivity_model = "wall_emissivity" ;
diffused_fraction = 0.9 ;
}
with a typical emissivity
model:
EMISSIVITY_MODEL( "wall_emissivity" ) {
type = constant ;
emissivity = 0.8 ;
}