降伏曲面
Drücker-Pragerの降伏曲面は次のとおりです。
(5)
F
=
q
−
r
c
(
p
)
⋅
(
p
tan
β
+
c
)
=
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOraiabg2
da9iaadghacqGHsislciGGYbWaaSbaaSqaaiaacogaaeqaaOWaaeWa
aeaacaWGWbaacaGLOaGaayzkaaGaeyyXIC9aaeWaaeaacaWGWbGaci
iDaiaacggacaGGUbGaeqOSdiMaey4kaSIaam4yaaGaayjkaiaawMca
aiabg2da9iaaicdaaaa@4B01@
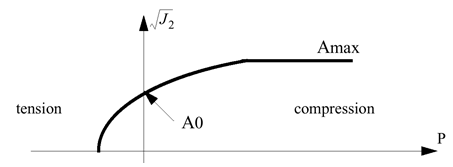
図 4.
この材料則で
p
a
<
p
<
p
b
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGHbaabeaakiabgYda8iaadchacqGH8aapcaWGWbWaaSba
aSqaaiaadkgaaeqaaaaa@3D0C@
によって考慮するキャップ硬化は次のように記述できます。
(6)
r
c
(
p
) =
1 −
(
p −
p
a
p
b
−
p
a
)
2
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciOCamaaBa
aaleaacaGGJbaabeaakmaabmaabaGaamiCaaGaayjkaiaawMcaaiab
g2da9maakaaabaGaaGymaiabgkHiTmaabmaabaWaaSaaaeaacaWGWb
GaeyOeI0IaamiCamaaBaaaleaacaWGHbaabeaaaOqaaiaadchadaWg
aaWcbaGaamOyaaqabaGccqGHsislcaWGWbWaaSbaaSqaaiaadggaae
qaaaaaaOGaayjkaiaawMcaamaaCaaaleqabaGaaGOmaaaaaeqaaaaa
@48CC@
圧縮力または引張り力が小さい場合は
p
≤
p
a
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaiabgs
MiJkaadchadaWgaaWcbaGaamyyaaqabaaaaa@3AA7@
が成り立つので、線形降伏曲面は次のように考慮されます。
(7)
r
c
(
p
)
=
1
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciOCamaaBa
aaleaacaGGJbaabeaakmaabmaabaGaamiCaaGaayjkaiaawMcaaiab
g2da9iaaigdaaaa@3C4A@
ここで、
q
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyCaaaa@36EC@
フォンミーゼス応力
q
2
=
3
J
2
=
3
2
s
i
j
2
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyCamaaCa
aaleqabaGaaGOmaaaakiabg2da9iaaiodacaWGkbWaaSbaaSqaaiaa
ikdaaeqaaOGaeyypa0ZaaSaaaeaacaaIZaaabaGaaGOmaaaacaWGZb
WaaSbaaSqaaiaadMgacaWGQbaabeaakmaaCaaaleqabaGaaGOmaaaa
aaa@41E6@
p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaaaa@36EB@
圧力
p
=
−
1
3
σ
i
j
=
−
1
3
I
1
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaiabg2
da9iabgkHiTmaalaaabaGaaGymaaqaaiaaiodaaaGaeq4Wdm3aaSba
aSqaaiaadMgacaWGQbaabeaakiabg2da9iabgkHiTmaalaaabaGaaG
ymaaqaaiaaiodaaaGaamysamaaBaaaleaacaaIXaaabeaaaaa@436C@
s
i
j
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4CamaaBa
aaleaacaWGPbGaamOAaaqabaaaaa@38F7@
偏差応力
s
i
j
=
σ
i
j
+
p
δ
i
j
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4CamaaBa
aaleaacaWGPbGaamOAaaqabaGccqGH9aqpcqaHdpWCdaWgaaWcbaGa
amyAaiaadQgaaeqaaOGaey4kaSIaamiCaiabes7aKnaaDaaaleaaca
WGPbaabaGaamOAaaaaaaa@4363@
c
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSbaaSqaai
aacogaaeqaaaaa@3709@
粘着
β
摩擦角
p
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaaIWaaabeaaaaa@37D1@
圧力値
∂ F
∂ p
(
p
0
) = 0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGgbaabaGaeyOaIyRaamiCaaaadaqadaqaaiaadchadaWg
aaWcbaGaaGimaaqabaaakiaawIcacaGLPaaacqGH9aqpcaaIWaaaaa@3FC0@
塑性流れ
塑性流れは、次のように定義される関連付けのない潜在的な流れ
G
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4raaaa@36C2@
次の場合;
p
≤
p
a
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaiabgs
MiJkaadchadaWgaaWcbaGaamyyaaqabaaaaa@3AA7@
(8)
G
=
q
−
p
⋅
tan
ψ
=
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4raiabg2
da9iaadghacqGHsislcaWGWbGaeyyXICTaciiDaiaacggacaGGUbGa
eqiYdKNaeyypa0JaaGimaaaa@4349@
次の場合;
p
a
<
p
≤
p
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGHbaabeaakiabgYda8iaadchacqGHKjYOcaWGWbWaaSba
aSqaaiaaicdaaeqaaaaa@3D90@
(9)
G
=
q
−
tan
ψ
(
p
−
(
p
−
p
a
)
2
2
(
p
0
−
p
a
)
)
=
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4raiabg2
da9iaadghacqGHsislciGG0bGaaiyyaiaac6gacqaHipqEdaqadaqa
aiaadchacqGHsisldaWcaaqaamaabmaabaGaamiCaiabgkHiTiaadc
hadaWgaaWcbaGaamyyaaqabaaakiaawIcacaGLPaaadaahaaWcbeqa
aiaaikdaaaaakeaacaaIYaWaaeWaaeaacaWGWbWaaSbaaSqaaiaaic
daaeqaaOGaeyOeI0IaamiCamaaBaaaleaacaWGHbaabeaaaOGaayjk
aiaawMcaaaaaaiaawIcacaGLPaaacqGH9aqpcaaIWaaaaa@511C@
p
>
p
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaiabg6
da+iaadchadaWgaaWcbaGaaGimaaqabaaaaa@39CE@
の場合(たとえば、流れがキャップ上で関連付けられるようになる場合)
(10)
G = F
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4raiabg2
da9iaadAeaaaa@3893@
∂
G
∂
p
(
p
0
)
=
∂
F
∂
p
(
p
0
)
=
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGhbaabaGaeyOaIyRaamiCaaaadaqadaqaaiaadchadaWg
aaWcbaGaaGimaaqabaaakiaawIcacaGLPaaacqGH9aqpdaWcaaqaai
abgkGi2kaadAeaaeaacqGHciITcaWGWbaaamaabmaabaGaamiCamaa
BaaaleaacaaIWaaabeaaaOGaayjkaiaawMcaaiabg2da9iaaicdaaa a@48D1@
定義上、潜在的な流れの方向は塑性ポテンシャルと直交しています。
(11)
d
ε
i j
p
= d Λ ⋅
∂ G
∂
σ
i j
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabew
7aLnaaDaaaleaacaWGPbGaamOAaaqaaiaadchaaaGccqGH9aqpcaWG
KbGaeu4MdWKaeyyXIC9aaSaaaeaacqGHciITcaWGhbaabaGaeyOaIy
Raeq4Wdm3aaSbaaSqaaiaadMgacaWGQbaabeaaaaaaaa@48B1@
一貫性および実験的な硬化と軟化を実現できるように、スカラー
d
Λ
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabfU
5ambaa@3854@
硬化と軟化
キャップは、以下に従って
p
a
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGHbaabeaaaaa@37FD@
が大きくなると仮定して、パラメータ
p
b
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGIbaabeaaaaa@37FE@
のみで定義します。
(12)
p
a
p
b
=
p
a 0
p
b 0
= α
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca
WGWbWaaSbaaSqaaiaadggaaeqaaaGcbaGaamiCamaaBaaaleaacaWG
IbaabeaaaaGccqGH9aqpdaWcaaqaaiaadchadaWgaaWcbaGaamyyai
aaicdaaeqaaaGcbaGaamiCamaaBaaaleaacaWGIbGaaGimaaqabaaa
aOGaeyypa0JaeqySdegaaa@437B@
ここで、
p
a
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGHbGaaGimaaqabaaaaa@38B7@
p
b
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGHbGaaGimaaqabaaaaa@38B7@
p
a
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGHbaabeaaaaa@37FD@
p
b
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGIbaabeaaaaa@37FE@
p
b
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGIbaabeaaaaa@37FE@
の変化は、入力
fct_ID pb で指定する曲線に基づいて
ε
v
p
=
−
ε
i
i
p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyTdu2aa0
baaSqaaiaadAhaaeaacaWGWbaaaOGaeyypa0JaeyOeI0IaeqyTdu2a
a0baaSqaaiaadMgacaWGPbaabaGaamiCaaaaaaa@405C@
に依存します。
注:
ε
v
p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyTdu2aa0
baaSqaaiaadAhaaeaacaWGWbaaaaaa@39BA@
と
p
b
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGIbaabeaaaaa@37FE@
でも同じ符号変換が考慮されます。これらは圧縮では正符号になります。
せん断降伏は
p
b
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGIbaabeaaaaa@37FE@
I soft
p
a
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGHbaabeaaaaa@37FD@
p
b
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGIbaabeaaaaa@37FE@
式 12 軟化が可能な場合は、条件
p
a
>
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGHbaabeaakiabg6da+iaaicdaaaa@39C9@
d
ε
v
p
≥ 0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabew
7aLnaaDaaaleaacaWG2baabaGaamiCaaaakiabgwMiZkaaicdaaaa@3D2D@
応力とひずみとの関係の導出
体積弾性率
K
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4saaaa@36C6@
とせん断弾性率
μ
を考慮して、偏差応力テンソルと偏差弾性ひずみテンソルとの関係、圧力と体積ひずみおよびその塑性成分との関係を記述します。
(13)
d
s
i
j
=
2
μ
(
d
e
i
j
−
d
e
i
j
p
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiaado
hadaWgaaWcbaGaamyAaiaadQgaaeqaaOGaeyypa0JaaGOmaiabeY7a
TnaabmaabaGaamizaiaadwgadaWgaaWcbaGaamyAaiaadQgaaeqaaO
GaeyOeI0IaamizaiaadwgadaqhaaWcbaGaamyAaiaadQgaaeaacaWG
WbaaaaGccaGLOaGaayzkaaaaaa@489A@
(14)
d p = − K (
d
ε
i i
− d
ε
i i
p
) = − K (
d
ε
i i
− d
ε
i i
p
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiaadc
hacqGH9aqpcqGHsislcaWGlbWaaeWaaeaacaWGKbGaeqyTdu2aaSba
aSqaaiaadMgacaWGPbaabeaakiabgkHiTiaadsgacqaH1oqzdaqhaa
WcbaGaamyAaiaadMgaaeaacaWGWbaaaaGccaGLOaGaayzkaaGaeyyp
a0JaeyOeI0Iaam4samaabmaabaGaamizaiabew7aLnaaBaaaleaaca
WGPbGaamyAaaqabaGccqGHsislcaWGKbGaeqyTdu2aa0baaSqaaiaa
dMgacaWGPbaabaGaamiCaaaaaOGaayjkaiaawMcaaaaa@56BA@
以下の点に注意します。
(15)
∂
G
∂
σ
i
j
=
−
1
3
∂
G
∂
p
δ
i
j
+
3
2
q
s
i
j
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGhbaabaGaeyOaIyRaeq4Wdm3aaSbaaSqaaiaadMgacaWG
QbaabeaaaaGccqGH9aqpcqGHsisldaWcaaqaaiaaigdaaeaacaaIZa
aaamaalaaabaGaeyOaIyRaam4raaqaaiabgkGi2kaadchaaaGaeqiT
dq2aa0baaSqaaiaadMgaaeaacaWGQbaaaOGaey4kaSYaaSaaaeaaca
aIZaaabaGaaGOmaiaadghaaaGaam4CamaaBaaaleaacaWGPbGaamOA
aaqabaaaaa@4FA7@
(16)
∂ F
∂
s
i j
=
∂ G
∂
s
i j
=
3
2 q
s
i j
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGgbaabaGaeyOaIyRaam4CamaaBaaaleaacaWGPbGaamOA
aaqabaaaaOGaeyypa0ZaaSaaaeaacqGHciITcaWGhbaabaGaeyOaIy
Raam4CamaaBaaaleaacaWGPbGaamOAaaqabaaaaOGaeyypa0ZaaSaa
aeaacaaIZaaabaGaaGOmaiaadghaaaGaam4CamaaBaaaleaacaWGPb
GaamOAaaqabaaaaa@4AE7@
塑性体積ひずみのインクリメント
d
ε
v
p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabew
7aLnaaDaaaleaacaWG2baabaGaamiCaaaaaaa@3AA3@
と相当塑性ひずみ
d
ε
d
p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabew
7aLnaaDaaaleaacaWG2baabaGaamiCaaaaaaa@3AA3@
および
d
Λ
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabfU
5ambaa@3854@
を関連付けできます。
(17)
d
ε
v
p
= d Λ
∂ G
∂ p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabew
7aLnaaDaaaleaacaWG2baabaGaamiCaaaakiabg2da9iaadsgacqqH
BoatdaWcaaqaaiabgkGi2kaadEeaaeaacqGHciITcaWGWbaaaaaa@42AE@
∂
G
∂
q
=
1
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGhbaabaGaeyOaIyRaamyCaaaacqGH9aqpcaaIXaaaaa@3C55@
d
ε
d
p
=
d
Λ
∂
G
∂
q
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabew
7aLnaaDaaaleaacaWGKbaabaGaamiCaaaakiabg2da9iaadsgacqqH
BoatdaWcaaqaaiabgkGi2kaadEeaaeaacqGHciITcaWGXbaaaaaa@429D@
★および
式 11 、
式 14 、
式 16 、
式 17 から
d
Λ
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabfU
5ambaa@3854@
について解くことで、次が得られます。
(18)
d
Λ
=
1
h
(
∂
F
∂
s
i
j
2
μ
d
e
i
j
−
∂
F
∂
p
K
d
ε
i
i
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabfU
5amjabg2da9maalaaabaGaaGymaaqaaiaadIgaaaWaaeWaaeaadaWc
aaqaaiabgkGi2kaadAeaaeaacqGHciITcaWGZbWaaSbaaSqaaiaadM
gacaWGQbaabeaaaaGccaaIYaGaeqiVd0MaamizaiaadwgadaWgaaWc
baGaamyAaiaadQgaaeqaaOGaeyOeI0YaaSaaaeaacqGHciITcaWGgb
aabaGaeyOaIyRaamiCaaaacaWGlbGaamizaiabew7aLnaaBaaaleaa
caWGPbGaamyAaaqabaaakiaawIcacaGLPaaaaaa@54A0@
ここで、
h = 3 μ + K
∂ F
∂ p
∂ G
∂ p
−
∂ F
∂ c
d c
d
ε
d
p
−
∂ G
∂ p
∂ F
∂
p
b
d
p
b
d
ε
v
p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiAaiabg2
da9iaaiodacqaH8oqBcqGHRaWkcaWGlbWaaSaaaeaacqGHciITcaWG
gbaabaGaeyOaIyRaamiCaaaadaWcaaqaaiabgkGi2kaadEeaaeaacq
GHciITcaWGWbaaaiabgkHiTmaalaaabaGaeyOaIyRaamOraaqaaiab
gkGi2kaadogaaaWaaSaaaeaacaWGKbGaam4yaaqaaiaadsgacqaH1o
qzdaqhaaWcbaGaamizaaqaaiaadchaaaaaaOGaeyOeI0YaaSaaaeaa
cqGHciITcaWGhbaabaGaeyOaIyRaamiCaaaadaWcaaqaaiabgkGi2k
aadAeaaeaacqGHciITcaWGWbWaaSbaaSqaaiaadkgaaeqaaaaakmaa
laaabaGaamizaiaadchadaWgaaWcbaGaamOyaaqabaaakeaacaWGKb
GaeqyTdu2aa0baaSqaaiaadAhaaeaacaWGWbaaaaaaaaa@6444@
これにより、式 18 ですべての項を計算できます。
p
≤
p
a
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaiabgs
MiJkaadchadaWgaaWcbaGaamyyaaqabaaaaa@3AA7@
∂
F
∂
p
=
−
tan
β
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGgbaabaGaeyOaIyRaamiCaaaacqGH9aqpcqGHsislciGG
0bGaaiyyaiaac6gacqaHYoGyaaa@40F7@
∂
F
∂
c
=
−
1
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGgbaabaGaeyOaIyRaam4yaaaacqGH9aqpcqGHsislcaaI
Xaaaaa@3D33@
∂
F
∂
p
b
=
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGgbaabaGaeyOaIyRaamiCamaaBaaaleaacaWGIbaabeaa
aaGccqGH9aqpcaaIWaaaaa@3D6F@
p
≥
p
a
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaiabgw
MiZkaadchadaWgaaWcbaGaamyyaaqabaaaaa@3AB8@
であれば、
(19)
∂
F
∂
p
=
−
(
tan
β
r
c
+
d
r
c
d
p
(
p
tan
β
+
c
)
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGgbaabaGaeyOaIyRaamiCaaaacqGH9aqpcqGHsisldaqa
daqaaiGacshacaGGHbGaaiOBaiabek7aIjaadkhadaWgaaWcbaGaam
4yaaqabaGccqGHRaWkdaWcaaqaaiaadsgacaWGYbWaaSbaaSqaaiaa
dogaaeqaaaGcbaGaamizaiaadchaaaWaaeWaaeaacaWGWbGaciiDai
aacggacaGGUbGaeqOSdiMaey4kaSIaam4yaaGaayjkaiaawMcaaaGa
ayjkaiaawMcaaaaa@531D@
∂
F
∂
c
=
−
r
c
(
p
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGgbaabaGaeyOaIyRaam4yaaaacqGH9aqpcqGHsislcaWG
YbWaaSbaaSqaaiaadogaaeqaaOWaaeWaaeaacaWGWbaacaGLOaGaay
zkaaaaaa@410B@
および
∂ F
∂
p
b
=
− p (
p −
p
a
)
r
c
p
b
(
p
b
−
p
a
)
2
(
p tan β + c
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGgbaabaGaeyOaIyRaamiCamaaBaaaleaacaWGIbaabeaa
aaGccqGH9aqpdaWcaaqaaiabgkHiTiaadchadaqadaqaaiaadchacq
GHsislcaWGWbWaaSbaaSqaaiaadggaaeqaaaGccaGLOaGaayzkaaaa
baGaamOCamaaBaaaleaacaWGJbaabeaakiaadchadaWgaaWcbaGaam
OyaaqabaGcdaqadaqaaiaadchadaWgaaWcbaGaamOyaaqabaGccqGH
sislcaWGWbWaaSbaaSqaaiaadggaaeqaaaGccaGLOaGaayzkaaWaaW
baaSqabeaacaaIYaaaaaaakmaabmaabaGaamiCaiGacshacaGGHbGa
aiOBaiabek7aIjabgUcaRiaadogaaiaawIcacaGLPaaaaaa@5890@
p
≤
p
a
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaiabgs
MiJkaadchadaWgaaWcbaGaamyyaaqabaaaaa@3AA7@
∂ G
∂ p
= − tan ψ
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGhbaabaGaeyOaIyRaamiCaaaacqGH9aqpcqGHsislciGG
0bGaaiyyaiaac6gacqaHipqEaaa@4125@
p
a
≤
p
≤
p
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaWGHbaabeaakiabgsMiJkaadchacqGHKjYOcaWGWbWaaSba
aSqaaiaaicdaaeqaaaaa@3E41@
であれば、
(20)
∂ G
∂ p
= − tan ψ
(
p
0
− p
)
(
p
0
−
p
a
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGhbaabaGaeyOaIyRaamiCaaaacqGH9aqpcqGHsislciGG
0bGaaiyyaiaac6gacqaHipqEdaWcaaqaamaabmaabaGaamiCamaaBa
aaleaacaaIWaaabeaakiabgkHiTiaadchaaiaawIcacaGLPaaaaeaa
daqadaqaaiaadchadaWgaaWcbaGaaGimaaqabaGccqGHsislcaWGWb
WaaSbaaSqaaiaadggaaeqaaaGccaGLOaGaayzkaaaaaaaa@4CF1@
p
≥
p
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaiabgw
MiZkaadchadaWgaaWcbaGaaGimaaqabaaaaa@3A8C@
∂ F
∂ p
=
∂ G
∂ p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGgbaabaGaeyOaIyRaamiCaaaacqGH9aqpdaWcaaqaaiab
gkGi2kaadEeaaeaacqGHciITcaWGWbaaaaaa@4035@
最後に、
d
q
d
p
=
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca
WGKbGaamyCaaqaaiaadsgacaWGWbaaaiabg2da9iaaicdaaaa@3B83@
によって次が得られます。
(21)
p
0
=
p
a
+
−
(
p
a
tan
β
+
c
)
+
(
p
a
tan
β
+
c
)
2
+
8
[
tan
β
(
p
b
−
p
a
)
]
2
4
tan
β
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaaIWaaabeaakiabg2da9iaadchadaWgaaWcbaGaamyyaaqa
baGccqGHRaWkdaWcaaqaaiabgkHiTmaabmaabaGaamiCamaaBaaale
aacaWGHbaabeaakiGacshacaGGHbGaaiOBaiabek7aIjabgUcaRiaa
dogaaiaawIcacaGLPaaacqGHRaWkdaGcaaqaamaabmaabaGaamiCam
aaBaaaleaacaWGHbaabeaakiGacshacaGGHbGaaiOBaiabek7aIjab
gUcaRiaadogaaiaawIcacaGLPaaadaahaaWcbeqaaiaaikdaaaGccq
GHRaWkcaaI4aWaamWaaeaaciGG0bGaaiyyaiaac6gacqaHYoGydaqa
daqaaiaadchadaWgaaWcbaGaamOyaaqabaGccqGHsislcaWGWbWaaS
baaSqaaiaadggaaeqaaaGccaGLOaGaayzkaaaacaGLBbGaayzxaaWa
aWbaaSqabeaacaaIYaaaaaqabaaakeaacaaI0aGaciiDaiaacggaca
GGUbGaeqOSdigaaaaa@6726@
p
<
p
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaiabgY
da8iaadchadaWgaaWcbaGaaGimaaqabaaaaa@39CA@
∂
G
∂
p
<
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGhbaabaGaeyOaIyRaamiCaaaacqGH8aapcaaIWaaaaa@3C51@
式 14 の最後の項は無意味です。これを実現するには、
∂
F
∂
p
b
=
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacq
GHciITcaWGgbaabaGaeyOaIyRaamiCamaaBaaaleaacaWGIbaabeaa
aaGccqGH9aqpcaaIWaaaaa@3D6F@
d
ε
v
p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabew
7aLnaaDaaaleaacaWG2baabaGaamiCaaaaaaa@3AA3@
d
ε
v
p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabew
7aLnaaDaaaleaacaWG2baabaGaamiCaaaaaaa@3AA3@
p
→
p
b
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaiabgk
ziUkaadchadaWgaaWcbaGaamOyaaqabaaaaa@3AE0@
d
r
c
d
p
→
∞
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca
WGKbGaamOCamaaBaaaleaacaWGJbaabeaaaOqaaiaadsgacaWGWbaa
aiabgkziUkabg6HiLcaa@3E40@
d
Λ
→
∞
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabfU
5amjabgkziUkabg6HiLcaa@3BB2@
式 17 で
d
ε
v
p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabew
7aLnaaDaaaleaacaWG2baabaGaamiCaaaaaaa@3AA3@
この場合は、偏差項が無視されるように、1次で特殊な処理が必要になります。
(22)
d
ε
v
p
=
−
d
ε
v
(
K
K
+
d
p
b
d
ε
v
p
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiabew
7aLnaaDaaaleaacaWG2baabaGaamiCaaaakiabg2da9iabgkHiTiaa
dsgacqaH1oqzdaWgaaWcbaGaamODaaqabaGcdaqadaqaamaalaaaba
Gaam4saaqaaiaadUeacqGHRaWkdaWcaaqaaiaadsgacaWGWbWaaSba
aSqaaiaadkgaaeqaaaGcbaGaamizaiabew7aLnaaDaaaleaacaWG2b
aabaGaamiCaaaaaaaaaaGccaGLOaGaayzkaaaaaa@4C3E@
d
e
i
j
p
=
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiaadw
gadaqhaaWcbaGaamyAaiaadQgaaeaacaWGWbaaaOGaeyypa0JaaGim
aaaa@3C92@
弾性プロパティ
キャップの降伏は、実際には圧縮プロセスのモデル化です。したがって、空隙率が小さくなると弾性プロパティは大きくなります。つまり、
ε
v
p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyTdu2aa0
baaSqaaiaadAhaaeaacaWGWbaaaaaa@39BA@
ε
v
p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyTdu2aa0
baaSqaaiaadAhaaeaacaWGWbaaaaaa@39BA@
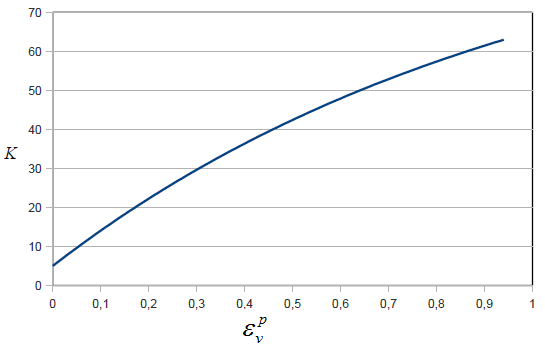
の変化に伴う
K
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4saaaa@36C6@
と
μ
の変化は、入力で指定する2つの関数で決まります。
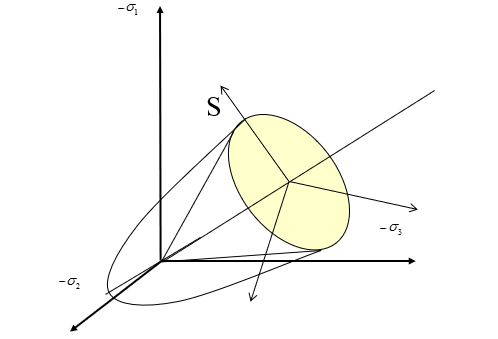
図 5.
注: 一般的に、可変の弾性プロパティを使用した場合、全面的な除荷後の硬化パラメータ
ε
v
p
=
∫
d
ε
v
p
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyTdu2aa0
baaSqaaiaadAhaaeaacaWGWbaaaOGaeyypa0Zaa8qaaeaacaWGKbGa
eqyTdu2aa0baaSqaaiaadAhaaeaacaWGWbaaaaqabeqaniabgUIiYd
aaaa@4167@
と体積デフォーメーションには一貫性がなくなります。
多孔質モデル 多孔質モデルは
2 にヒントを得たモデルであり、空隙のある弾性粒状物で土が構成されていると仮定しています。エネルギーが少なく、完全には圧縮していない土に適用します。大きなエネルギーで完全に圧縮した土では状態方程式を使用する必要があります。この材料則では、空隙の体積変化に弾性部分と塑性部分があります。弾性部分は、スケルトンの弾性デフォーメーションに起因して発生します。塑性部分は粒状物の再配置に相当し、圧力載荷による圧縮を誘発するほか、せん断載荷が進行している場合はダイラタンシーも誘発します。
注: 空気の存在は、このモデルの構成要素になりません。空隙率は、全参照体積にボイドが占める体積の比率として定義します。
(23)
n
=
V
v
o
i
d
V
t
o
t
a
l
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
GaamOBaiabg2da9iaacckadaWcaaWdaeaapeGaamOva8aadaWgaaWc
baWdbiaadAhacaWGVbGaamyAaiaadsgaa8aabeaaaOqaa8qacaWGwb
WdamaaBaaaleaapeGaamiDaiaad+gacaWG0bGaamyyaiaadYgaa8aa
beaaaaaaaa@445F@
弾性材料ではボイドの体積は変化しません。一方、塑性材料では、空隙率の変化を次のように定義します。
(24)
n
=
1
−
(
1
−
n
0
)
e
ε
v
p
−
ε
v
0
p
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaqaaaaaaaaa
Wdbiaad6gacqGH9aqpcaaIXaGaeyOeI0YaaeWaa8aabaWdbiaaigda
cqGHsislcaWGUbWdamaaBaaaleaapeGaaGimaaWdaeqaaaGcpeGaay
jkaiaawMcaaiaadwgapaWaaWbaaSqabeaapeGaeqyTdu2damaaDaaa
meaapeGaamODaaWdaeaapeGaamiCaaaaliabgkHiTiabew7aL9aada
qhaaadbaWdbiaadAhacaaIWaaapaqaa8qacaWGWbaaaaaaaaa@4A7F@
孔の初期状態は、初期空隙率、初期飽和度、および初期孔圧力で定義します。飽和度は、次のように空隙体積に対する水分体積の比率として定義します。
(25)
S
=
V
w
a
t
e
r
V
v
o
i
d
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
Gaam4uaiabg2da9iaacckadaWcaaWdaeaapeGaamOva8aadaWgaaWc
baWdbiaadEhacaWGHbGaamiDaiaadwgacaWGYbaapaqabaaakeaape
GaamOva8aadaWgaaWcbaWdbiaadAhacaWGVbGaamyAaiaadsgaa8aa
beaaaaaaaa@4443@
上記の空隙は、水で部分的に満たされていても、全体が満たされていてもかまいません。土質力学では、土が飽和していない
S
<
1
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiabgY
da8iaaigdaaaa@388E@
u
=
0
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyDaiabg2
da9iaaicdaaaa@38B1@
S
≥
1
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uaiabgw
MiZkaaigdaaaa@3950@
u
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyDaaaa@36F1@
3
p
=
p
'
+
u
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaiabg2
da9iaadchadaahaaWcbeqaaiaacEcaaaGccqGHRaWkcaWG1baaaa@3BA5@
p
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCaaaa@36EC@
空隙の平均密度は、水の質量を空隙の体積で除算して求めることができます。
(26)
ρ
v
o
i
d
=
m
w
a
t
e
r
V
v
o
i
d
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyWdi3aaS
baaSqaaiaadAhacaWGVbGaamyAaiaadsgaaeqaaOGaeyypa0ZaaSaa
aeaacaWGTbWaaSbaaSqaaiaadEhacaWGHbGaamiDaiaadwgacaWGYb
aabeaaaOqaaiaadAfadaWgaaWcbaGaamODaiaad+gacaWGPbGaamiz
aaqabaaaaaaa@477A@
次に以下を定義します。
(27)
μ
w
=
ρ
v
o
i
d
ρ
w
0
−
1
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape
GaeqiVd02damaaBaaaleaapeGaam4DaaWdaeqaaOGaeyypa0ZaaSaa
aeaacqaHbpGCdaWgaaWcbaGaamODaiaad+gacaWGPbGaamizaaqaba
aakeaacqaHbpGCdaWgaaWcbaGaam4DaiaaicdaaeqaaaaakiabgkHi
Tiaaigdaaaa@4548@
ρ
w
0
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb
a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr
0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabeg8aYnaaBa
aaleaacaWG3bGaaGimaaqabaaaaa@398E@
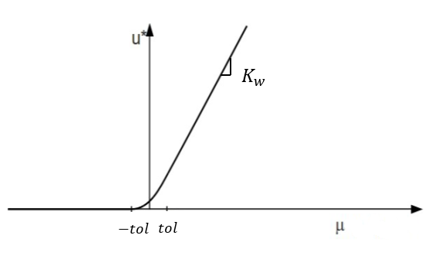
安定性を確保するために粘性項を追加します。
μ
w
>
−
t
o
l
then
u
v
i
s
=
−
α
v
K
w
ρ
(
V
o
l
)
1
3
ε
v
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8
qacqaH8oqBpaWaaSbaaSqaa8qacaWG3baapaqabaGcpeGaeyOpa4Ja
eyOeI0IaaiiOaiaadshacaWGVbGaamiBaiaabccacaqG0bGaaeiAai
aabwgacaqGUbGaaeiiaiaadwhapaWaaSbaaSqaa8qacaWG2bGaamyA
aiaadohaa8aabeaak8qacqGH9aqpcaGGGcGaeyOeI0IaeqySde2dam
aaBaaaleaapeGaamODaaWdaeqaaOWdbmaakaaapaqaa8qacaWGlbWd
amaaBaaaleaapeGaam4DaaWdaeqaaOWdbiaacckacqaHbpGCaSqaba
GccaGGGcWaaeWaa8aabaWdbiaadAfacaWGVbGaamiBaaGaayjkaiaa
wMcaa8aadaahaaWcbeqaa8qadaWcaaWdaeaapeGaaGymaaWdaeaape
GaaG4maaaaaaGccaGGGcGaeqyTdu2damaaBaaaleaapeGaamODaaWd
aeqaaaaa@5FD8@
u
*
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyDamaaCa
aaleqabaGaaiOkaaaaaaa@37CB@
スムーズな遷移にするために以下を定義します。
(28)
If
μ
w
<
−
t
o
l
:
u
*
=
0
If
|
μ
w
|
<
t
o
l
:
u
*
=
K
w
4
t
o
l
(
μ
w
+
t
o
l
)
2
If
μ
w
>
t
o
l
:
u
*
=
K
w
μ
w
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaaqaaaaa
aaaaWdbiaabMeacaqGMbGaaeiiaiabeY7aT9aadaWgaaWcbaWdbiaa
dEhaa8aabeaak8qacqGH8aapcqGHsislcaWG0bGaam4BaiaadYgaca
GG6aGaamyDa8aadaahaaWcbeqaa8qacaGGQaaaaOGaeyypa0JaaiiO
aiaaicdaaeaacaqGjbGaaeOzaiaabccadaabdaWdaeaapeGaeqiVd0
2damaaBaaaleaapeGaam4DaaWdaeqaaaGcpeGaay5bSlaawIa7aiab
gYda8iaadshacaWGVbGaamiBaiaacQdacaWG1bWdamaaCaaaleqaba
WdbiaacQcaaaGccqGH9aqpcaGGGcWaaSaaa8aabaWdbiaadUeapaWa
aSbaaSqaa8qacaWG3baapaqabaaakeaapeGaaGinaiaadshacaWGVb
GaamiBaaaacaGGGcWaaeWaa8aabaWdbiabeY7aT9aadaWgaaWcbaWd
biaadEhaa8aabeaak8qacqGHRaWkcaWG0bGaam4BaiaadYgaaiaawI
cacaGLPaaapaWaaWbaaSqabeaapeGaaGOmaaaaaOWdaeaapeGaaeys
aiaabAgacaqGGaGaeqiVd02damaaBaaaleaapeGaam4DaaWdaeqaaO
GaeyOpa4ZdbiaadshacaWGVbGaamiBaiaacQdacaWG1bWdamaaCaaa
leqabaWdbiaacQcaaaGcpaGaeyypa0ZdbiaacckacaWGlbWdamaaBa
aaleaapeGaam4DaaWdaeqaaOWdbiaacckacqaH8oqBpaWaaSbaaSqa
a8qacaWG3baapaqabaaaaaa@7D59@
K
w
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaaeaaaaaaaaa8
qacaWGlbWdamaaBaaaleaapeGaam4DaaWdaeqaaaaa@383C@
は水の体積弾性率です。
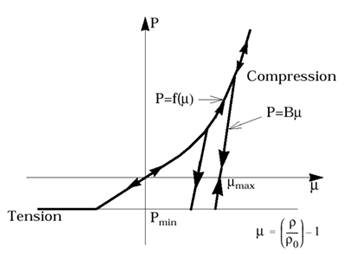
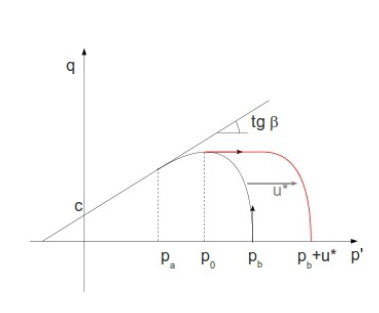
図 6. 空隙に起因する圧力
p
0
≤
p
'
≤
p
0
+
u
*
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaaBa
aaleaacaaIWaaabeaakiabgsMiJkaadchadaahaaWcbeqaaiaacEca
aaGccqGHKjYOcaWGWbWaaSbaaSqaaiaaicdaaeqaaOGaey4kaSIaam
yDamaaCaaaleqabaGaaiOkaaaaaaa@41B9@
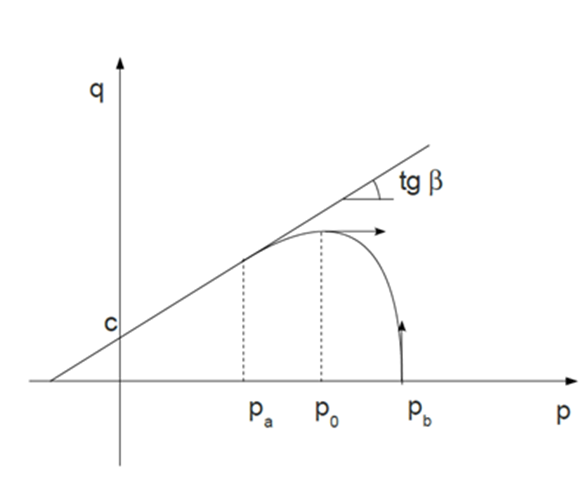
となるように、純粋なvon Mises領域を追加することによってキャップを変更します。
図 7. キャップの変更