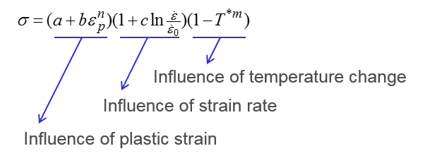
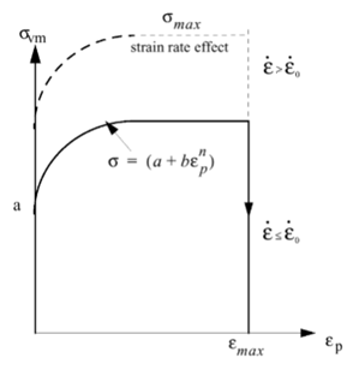
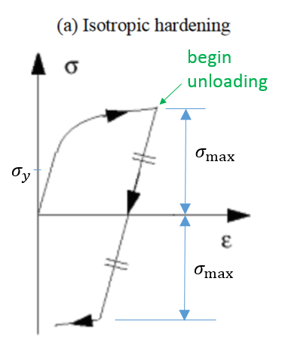
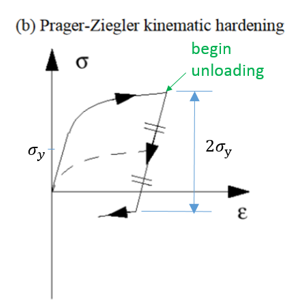
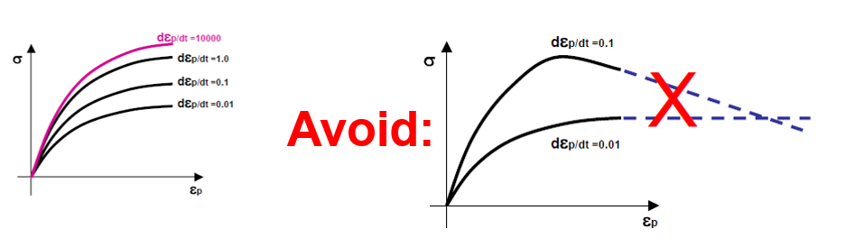
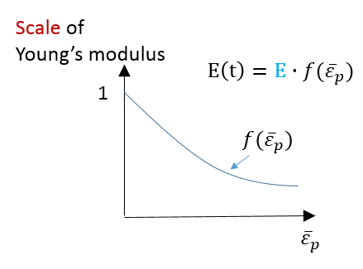
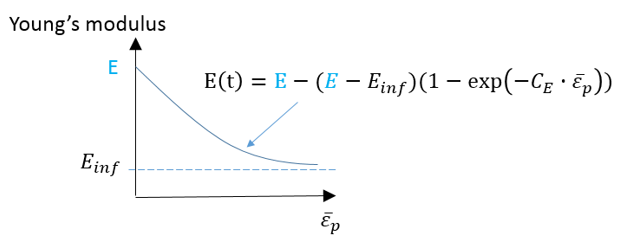
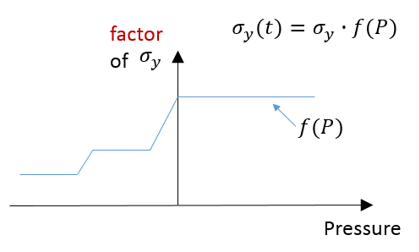
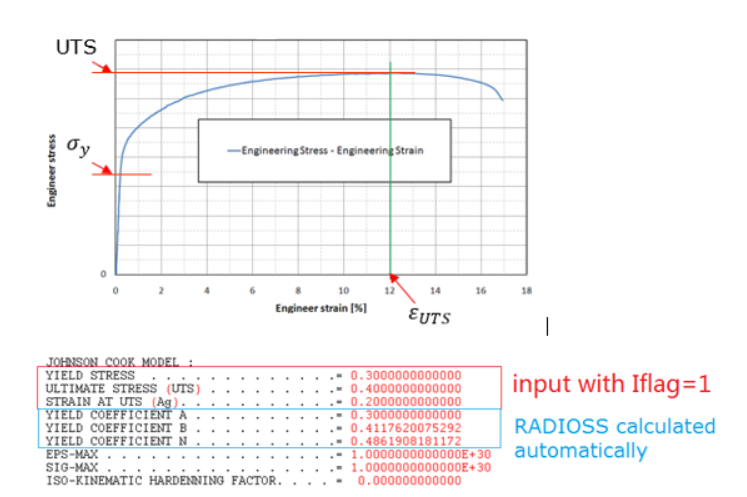
Radioss材料則では、LAW32、LAW43、LAW72、LAW73、LAW74、LAW78およびLAW93はHILL基準を使用します。
ひずみ比
ランクフォードパラメータ
は、面内の塑性ひずみと厚み方向の塑性ひずみ
との比率です。
(11)
ここで、は、直交異方性方向1に対して成す角度です。
は、直交方向1の異なる角度で切断した異なる試料で測定することができます。は荷重方向が直交方向1に沿った引張試験から測定され、 は荷重が直交方向1に直交する引張試験から測定されます。
ひずみ比は、試料の幅方向のひずみと試料の厚さ方向のひずみとの比です。
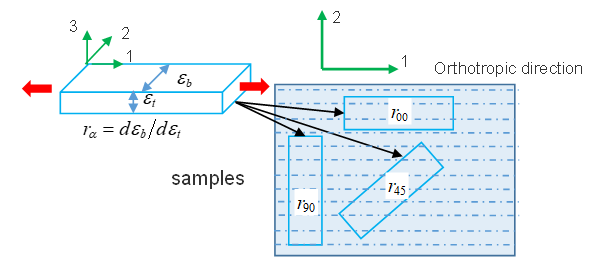
図 10.
この場合、HILLパラメータは:
(12)
(13)
(14)
(15)
ここで、
LAW32、LAW43およびLAW73では、HILL基準は:
(16)
|
|
|
|
|
|
これらはすべてランクフォードパラメータ(ひずみ比)を要求し、HILLパラメータはRadiossによって自動的に計算されます。
降伏応力比
LAW93では、使用される降伏応力比は:
(17)
降伏応力比
を得るには2つの荷重ケースでの降伏応力を測定する必要があります。
- 引張試験からの降伏応力
- せん断試験からの降伏せん断応力
LAW93では、パラメータ入力が使用されている場合は初期応力パラメータを基準降伏応力 とします。曲線入力を使用する場合は、曲線からの降伏応力を基準降伏応力 とします。
シェル用の4つのHILLパラメータが
Radiossによって自動的に計算されます。
(18)
(19)
(20)
(21)
LAW74では、降伏応力比
は降伏応力
および
入力と直接使用され、ソリッド用の6つのHILLパラメータが
Radiossによって自動的に計算されます。
|
|
|
|
|
|
シェル要素の場合、、とします。