ACU-T: 5402 Piezoelectric Flow Energy Harvester with Rigid Body Rotation
This tutorial provides the instructions for setting up, solving and viewing results for a simulation of a piezoelectric fluid harvester. In this simulation, a piezoelectric flow harvester is placed in a fluid flow channel. The harvester is attached to a cylinder mount which also acts as a bluff body causing vortices in the fluid flow. In addition, the cylinder and the harvester are imparted with a sinusoidal rotation motion. The interaction between the pressure fields generated by the vortices and the flow harvester structure is simulated in this tutorial. Arbitrary Lagrangian Eulerian (ALE) approach is used to compute the mesh deformation in the fluid domain as it interacts with the deforming structure.
- Defining rigid body rotation motion
- Implementation of P-FSI in conjunction with rigid body rotation
- Analyze the problem
- Start AcuConsole and read the simulation database of the Piezoelectric Flow Harvester
- Modify general problem parameters
- Create multiplier function for rigid body mesh motion
- Create mesh motion for rigid body rotation
- Apply mesh motion to the surface attributes
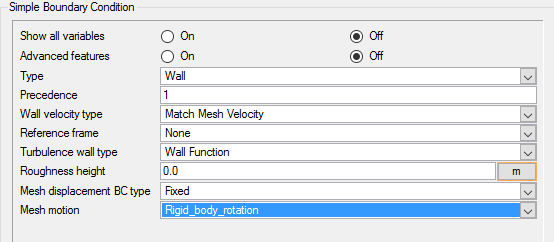
- Assign rigid body motion to the surface and node attributes
- Change the inlet velocity
- Add a time history output point
- Run AcuSolve
- Monitor the solution with AcuProbe
- Post-processing the nodal output with AcuFieldView
Prerequisites
You should have already run through the tutorials ACU-T: 2000 Turbulent Flow in a Mixing Elbow and ACU-T: 5400 Piezoelectric Flow Energy Harvester: A Fluid-Structure Interaction (P-FSI). It is assumed that you have some familiarity with AcuConsole, AcuSolve and AcuFieldView. You will also need access to a licensed version of AcuSolve.
Prior to running through this tutorial, copy AcuConsole_tutorial_inputs.zip from <Altair_installation_directory>\hwcfdsolvers\acusolve\win64\model_files\tutorials\AcuSolve to a local directory. Extract piezo_harvester_P-FSI.acs from AcuConsole_tutorial_inputs.zip. The file piezo_harvester_P-FSI.acs stores the complete setup as described in Piezoelectric Flow Harvester, which includes purely flexible body simulation. In this tutorial, you will start from that database and add a rigid body rotation and then simulate the flow phenomenon.
Analyze the Problem
An important step in any CFD simulation is to examine the engineering problem at hand and determine the important parameters that need to be provided to AcuSolve.
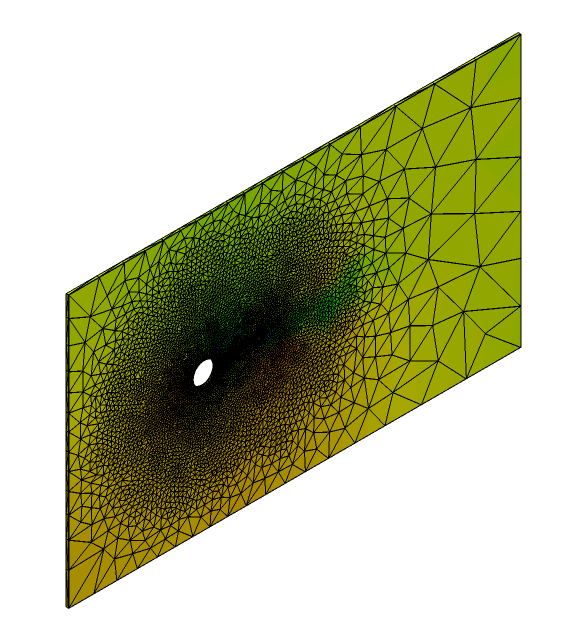
The CFD model contains a cantilever beam and a rigid cylindrical body. The beam along with the cylinder is placed in a water flow stream. This cylindrical body acts a bluff body placed in the flow and stimulates vortex shedding in the flow downstream as it passes over the cylinder. The alternating shedding of vortices creates a zone of alternating asymmetric pressure distribution on either side of the beam. Such an alternating pressure distribution exerts an oscillating force on the beam, creating a sustainable oscillating vibration in the beam.
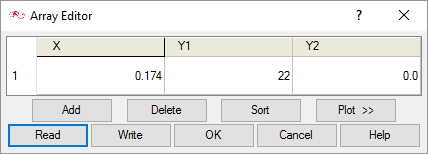
In this tutorial, in the addition to the flexible motion of the beam adopted in Piezoelectric Flow Harvester Tutorial-1, you will incorporate the rigid body rotation of the cylinder and the beam. The cylinder and the beam are enforced with a sinusoidal oscillatory rotation about the center of the cylinder with a maximum angle of rotation as 100 (i.e. 0.174 rad) with a frequency of 22 rad/sec (3.5 Hz). The axis of rotation is along axis of cylinder. The variation of the rotation angle (θ) is given as:
Where, t is the time (sec).
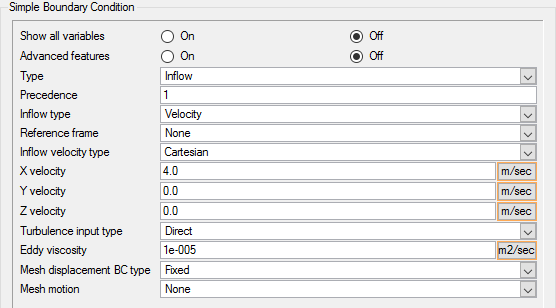
Since this tutorial has a rotation motion in addition to flexible motion of beam, you can achieve higher displacements (and hence strains) at lower velocity. Therefore, you will reduce the inlet velocity to 4 m/sec instead of 10 m/sec in Piezoelectric Flow Harvester Tutorial-1.

Figure 1. Schematic of the Problem

Figure 2. The Beam with its Various Layers
Define the Simulation Parameters
Start AcuConsole and Open the Simulation Database
In the next steps you will start AcuConsole and open a database that is set up for a P-FSI simulation of a non-rotating piezoelectric harvester. You will then make appropriate changes to the database to take into account the rigid body rotation of the harvester in addition to the flexible body motion.
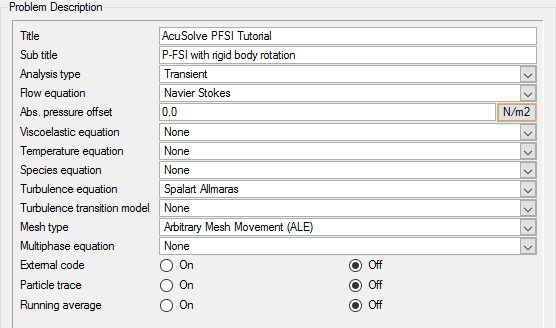
Set General Simulation Attributes
In the next steps you will modify global settings needed for the rigid body rotation of the piezoelectric harvester.
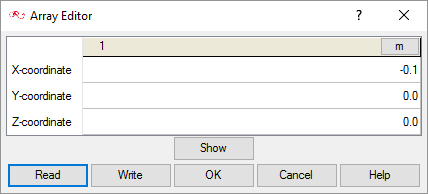
Create a Multiplier Function for Mesh Motion
The variation of the rotation angle () is modeled using a multiplier function using the following steps.
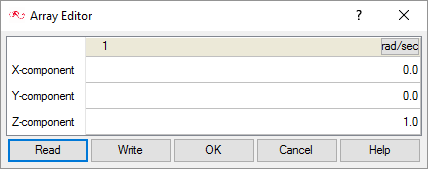
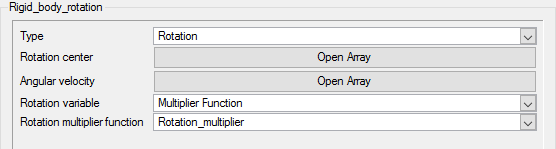
Create Mesh Motion for Rigid Body Rotation
In the next steps you will define the rigid body rotation of the cylinder and the beam.
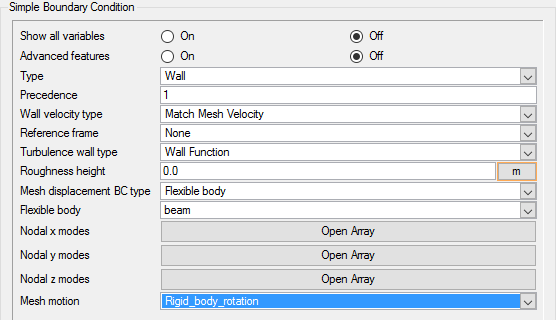
Assign Rigid Body Motion to the Beam Surface
Assign Rigid Body Motion to the Cylinder Surface
Reduce the Inlet Velocity
As mentioned in Analyze the Problem, you will set the inlet velocity to 4 m/sec.
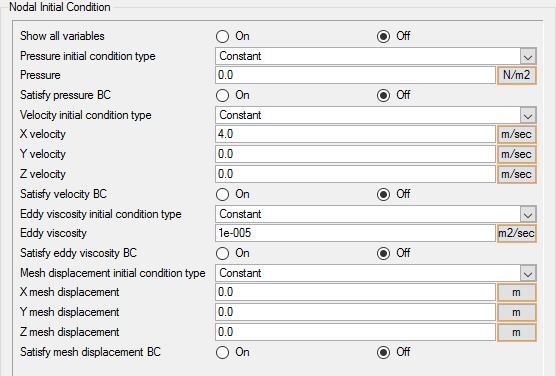
Set Initial Conditions
In the next steps you will set the initial conditions.
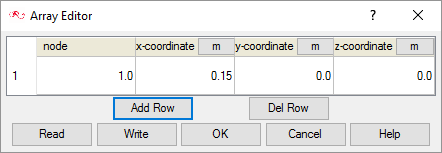
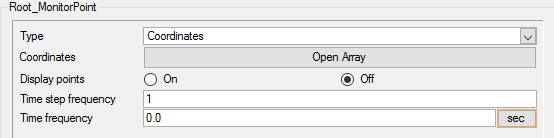
Add Time History Output Point
Time History Output commands enables you to extract the nodal solution at any point within the domain. In this simulation, it would be interesting to observe the displacement at the tip and root of the cantilever beam. The .acs database you started with has a monitor point at the tip of the cantilever beam.
The following steps will create a similar monitor point at the root of the cantilever beam.
Compute the Solution and Review the Results
Run AcuSolve
In the next steps you will launch AcuSolve to compute the solution for this case.
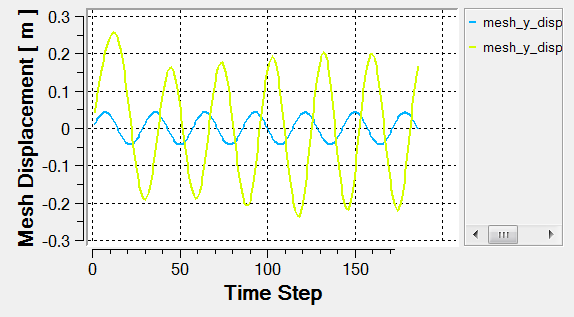
Post-Process with AcuProbe
AcuProbe can be used to monitor various variables over solution time.
Post-Process with AcuFieldView
- How to find the data readers in the File menu and open up the desired reader panel for data input.
- How to find the visualization panels either from the Side toolbar or the Visualization panel on the Main menu to create and modify surfaces in AcuFieldView.
- How to move the data around the modeling window using mouse actions to translate, rotate and zoom in to the data.
Start AcuFieldView
Figure 18.
Set Up AcuFieldView
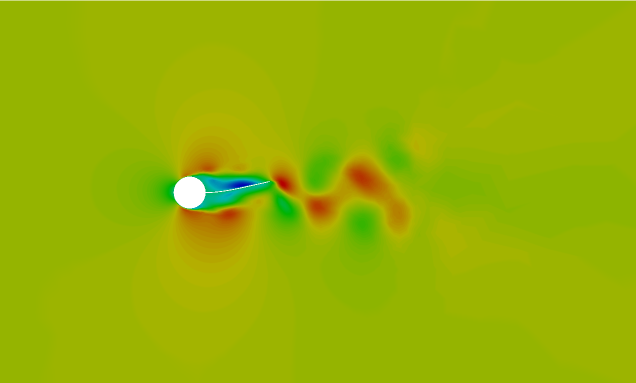
Visualize and Save an Animation of the Beam Displacement
Summary
In this tutorial you worked through a basic workflow to set up a flexible body motion of a rotating beam in the wake of a cylinder. You started with the piezo_harvester_P-FSI.acs file from the tutorial Piezoelectric Flow Harvester and modified the set up to accommodate the rigid body rotation of the beam and the cylinder. Once the case was set up, you generated a solution using AcuSolve. Results were post-processed in AcuFieldView to allow you to create animation of the beam displacements with time.
- Creating rigid body type mesh motion for rotation
- Implementation of P-FSI in conjunction of rigid body rotation