Basic Boundary Layer Theory

Velocity Boundary Layer

Velocity boundary layer or commonly referred to as boundary layer is a thin layer of fluid formed near a boundary surface where the viscous effects of the fluid are significant.

When a fluid moves past an object or an object moves past a fluid, the fluid molecules right next to the boundary surface stick to it. This causes the molecules just above the surface to slow down because of collision with the molecules sticking to the surface. These molecules consequently slow down the flow just above them. As we move farther away from the surface of the object, the collisions affected by the object’s surface reduces. Thus a layer of fluid is created within which the velocity of the flow gradually changes from zero at the object’s surface to the free stream velocity at a certain distance away from the surface.

This distance at which the flow velocity inside the boundary essentially reaches the free stream velocity is termed as the boundary layer thickness. Mathematically it is defined as the distance at which the flow velocity is 99 percent of the free stream velocity.

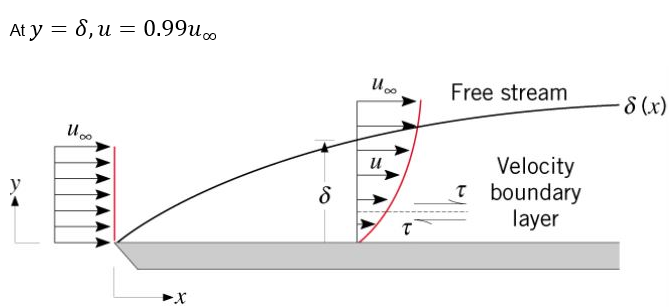
Figure 1. Velocity Boundary Layer

Thermal Boundary Layer

Thermal boundary layer is a region of fluid flow near a solid surface characterized by temperature gradients and heat fluxes. It is a consequence of heat transfer between the fluid and the solid surface and the fluid temperatures are directly influenced by heating or cooling from the surface wall.

The distance at which the difference between the flow temperatures inside the boundary layer and the boundary surface essentially reaches the difference between free stream temperature and the boundary surface temperature is termed as the thermal boundary layer thickness. It is mathematically expressed as:

At y = ${\delta }_t$ , $\frac{T_s-T}{T_s-T_{\infty }}$ = 0.99

Figure 2. Thermal Boundary Layer

Laminar Boundary Layer Flow

The flow inside a laminar boundary layer is smooth and takes place in layers. Each layer slides past the adjacent layers and any exchange of mass or momentum takes place only between these layers on a microscopic scale. Laminar boundary layer is formed when the Reynolds number is low.

The shear stresses associated with this flow can be calculated using the molecular viscosity $\mu$ .

Figure 3 depicts the typical velocity profile for a laminar boundary layer.

Figure 3. Laminar Boundary Layer

Turbulent Boundary Layer Flow

As the name suggests turbulent boundary layer flow is more chaotic and is characterized by active mixing of the fluid and momentum across several layers. The exchange of mass, momentum and energy takes place on a macroscopic scale with packets of fluid moving across the layers. A turbulent boundary layer is formed only at high Reynolds number.

In this case the scales of mixing cannot be handled by molecular viscosity alone, therefore turbulent or eddy viscosity has to be modeled in order to proceed with the calculations.

Figure 4 depicts the velocity profile for the turbulent boundary layer.

Figure 4. Turbulent Boundary Layer

The velocity profile for a turbulent boundary layer is quite different from a laminar boundary layer. It comprises of three regions or layers:

• Outer layer: This layer is sensitive to the properties of the external flow.
• Inner layer: This layer has turbulent mixing as the dominant physics.
• Laminar or viscous sublayer: This layer is attached to the wall where the no slip condition is applied. The shear stress in this layer is dominated by molecular viscosity.

Figure 5. Complete Boundary Layer Profile (Laminar and Turbulent)

These layers blend into each other and the blending region between the inner layer and laminar sublayer is termed as the Buffer Zone.

As a consequence of intense mixing, a turbulent boundary layer has a much steeper gradient of velocity resulting in a larger shear stress and higher skin friction drag at the wall compared to a laminar boundary layer. In addition heat transfer rates are higher for a turbulent boundary layer. The presence of eddies brings fluid particles at different temperatures into close contact with each other and the heat transfer comes more effective.

Another consequence of mixing is that a turbulent boundary layer has higher momentum near the wall, so it can withstand adverse pressure gradient longer and is less easily driven by the changes in the free stream pressure compared to a laminar boundary layer. This property allows a turbulent boundary layer to be attached to the object surface longer.

Boundary Layer Separation

Boundary layer separation is defined as the detachment of the boundary layer from the surface of the object thus leading to formation of eddies and vortices in the wake. The most important factor which leads to boundary layer separation is an adverse pressure gradient.

The pressure gradient is one of the parameters that greatly influences a flow. The shear stress caused by viscosity, near an object surface, has a retarding effect on the flow. This retardation can be overcome by a implementing a negative pressure gradient in the direction of the flow. A negative pressure gradient is termed as a favourable pressure gradient because it enables the flow.

Figure 6. Boundary Layer Separation

A positive pressure gradient, termed as adverse pressure gradient, has the opposite effect on the flow. It further retards the flow leading to a reduction in the velocity near the wall and an increased boundary layer thickness. This continuous retardation causes the shear stress at the wall to drop to zero which then becomes negative causing a reversal in the flow direction near the surface. A region of recirculating flow is developed with formation of large slowly rotating eddies resulting in the flow detaching from the surface of the object. The point at which the velocity gradient and essentially the shear stress reaches zero is termed as the point of separation.

The separation leads to the formation of a large wake of vortices behind the body, where the fluid pressure is much lower compared to the regions where the fluid is attached to the surface since the eddies cannot convert the rotational energy into pressure head. As described in the previous section the flow velocity near the object surface is higher in case of a turbulent boundary layer. This higher fluid momentum means that the fluid separation occurs further downstream than in case of a laminar boundary layer when subject to the same adverse pressure gradient, resulting in a narrower wake and consequently less pressure drag.

Figure 7. Boundary Layer Separation in a Diverging Channel (source: National committee for Fluid Mechanics Films; http://web.mit.edu/hml/ncfmf.html)

Figure 7 shows the separation of a laminar (top) and turbulent boundary (bottom) layer in a diverging channel.

Depending on the flow conditions, the recirculating flow may reattach to the surface of the body. A number of factors could influence the reattachment. The pressure gradient may turn favourable due to changing flow conditions or the geometry of the body. The other factor is that the boundary layer may transition from laminar to turbulent resulting in a fuller velocity profile that could sustain the adverse pressure gradient and causing the flow to reattach.

Boundary Layer Transition

These factors along with many other sources of disturbance can cause a smooth laminar flow to break down, enter a transition region and then develop into a turbulent flow. The mechanisms through which a boundary layer transitions can be one of the following:

• Natural transition: This mechanism is prevalent in weak disturbance environments (vibrations, free stream turbulence, adverse pressure gradient, and so on, are absent). The transition occurs gradually and breakdown is reached thorough a linear growth of disturbances. This mechanism is most commonly observed in the flow around a transport aircraft in flight.
• Bypass transition: This mechanism is observed in cases where the initial disturbances in the laminar flow are sufficiently high, caused by factors like surface roughness or high free stream turbulence. The highly non-linear growth of disturbances results in the quick formation of turbulent spots in the flow leading to breakdown, thus bypassing the linear mechanism. This transition mechanism is observed in flows related to turbomachinery where there is high free stream turbulence present.
• Intermediate mechanisms: Aside from the primary mechanisms of turbulence discussed above, there are additional intermediate mechanisms. They include spanwise modulations in the flow, distortions leading to secondary instabilities and direct bypass.

Importance and Practical Applications of Boundary Layer

Aside from the topics discussed above, there are numerous cases where the boundary layer and the physics associated with it have significant applications. A few examples are natural boundary layer in the atmosphere, biometrics of marine organisms, automobile aerodynamics and design of sports merchandise such as golf balls.